Zadanie
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Adamovi Královi na [email protected]
Táto úloha nadväzuje na úlohu Receptomaty z prechádzajúceho kola. Pri riešení tejto úlohy preto môžete využívať vzorové riešenie z minula.
Čarodejnice(a čarodejníci) vám to síce nechceli povedať, ale kniha receptomatov má druhú časť s názvom “Nerozhodné receptomaty”. Nechceli vám to povedať, pretože týmto receptomatom nerozumeli. Šípky zo stavov nedávajú veľmi zmysel - niekedy je ich viac ako jedna, čiže čarodejníci sa nevedeli dohodnúť, po ktorej majú ísť. Nakoniec však rozlúštili túto záhadu a popis k týmto receptomatom vám pridali do tutoriálu. Ten vám zase oskenovali a zdieľali na tejto adrese. Aby vám pomohli ešte viac, updatovali aj simulátor receptomatu. Ten je na tejto adrese.
Zároveň potrebujú od vás znovu pomoc.
Úloha
Niektoré strany z knihy receptomatov chýbajú. Pomôžte nájsť:
(2 body) Nerozhodný receptomat, ktorý akceptuje reťazce s podreťazcom
abac. Poznámka: táto úloha je rovnaká ako v prvej časti, typ receptomatu však výrazne zjednodušuje riešenie.(2 body) Receptomat, ktorý akceptuje čísla deliteľné číslom \(11\). (môže byť nerozhodný alebo rozhodný)
(2 body) Nerozhodný receptomat, ktorý akceptuje reťazce končiace sa na
aa.(2 body) Receptomat z c, ale aby bol rozhodný.
(2 body) Nerozhodný receptomat, ktorý akceptuje čísla deliteľné číslom \(25\).
(2 body) Receptomat z e, ale aby bol rozhodný.
(3 body) Aké recepty akceptuje tento receptomat? Dokážete z neho spraviť rozhodný receptomat?
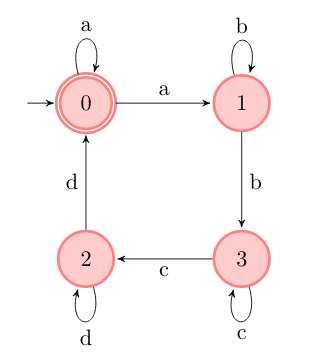
Podúlohy a, c, d sú z kapitoly “Písmenné receptomaty”. V týchto receptoch sa používajú len znaky a, b, c a d. Podúlohy b, e, f sú z kapitoly “Číselné receptomaty”. V týchto sa používajú znaky 0 až 9.
Podúloha a)
Keďže náš receptomat je nerozhodný, stačí nám držať ukazovateľ na počiatočnom stave a do ďalšieho prejsť pri vyhovujúcom znaku. Posledný stav má prechod do seba so všetkými znakmi – keď raz zistíme že sa na vstupe podreťazec abac nachádza, chceme si túto informáciu držať až do konca (pomocou akceptovaného stavu).

Podúloha b)
Toto bola ťažšia úloha ako sa na prvý pohľad zdalo. Deliteľnosť číslom 11 je ekvivalentná s deliteľnosťou rozdielu súčtov cifier na párnych a nepárnych miestach (napr. pre 6 ciferné číslo nás zaujíma (súčet cifier na prvom, treťom a piatom mieste) mínus (súčet cifier na druhom, štvrtom a šiestom mieste)). Budeme si teda držať aktuálny zvyšok po delení 11 a striedavo pričítavať/odčítavať cifry (príklad: číslo 14641 = +1-4+6-4+1 = 0, číslo je deliteľné 11). Budeme mať teda 11 stavov pre reprezentáciu aktuálneho zvyšku po delení, ale potrebujeme si aj pamätať či odčítavame alebo pričítavame (teda 2*11 = 22 stavov). Následne medzi nimi už len urobíme všetky prechody.
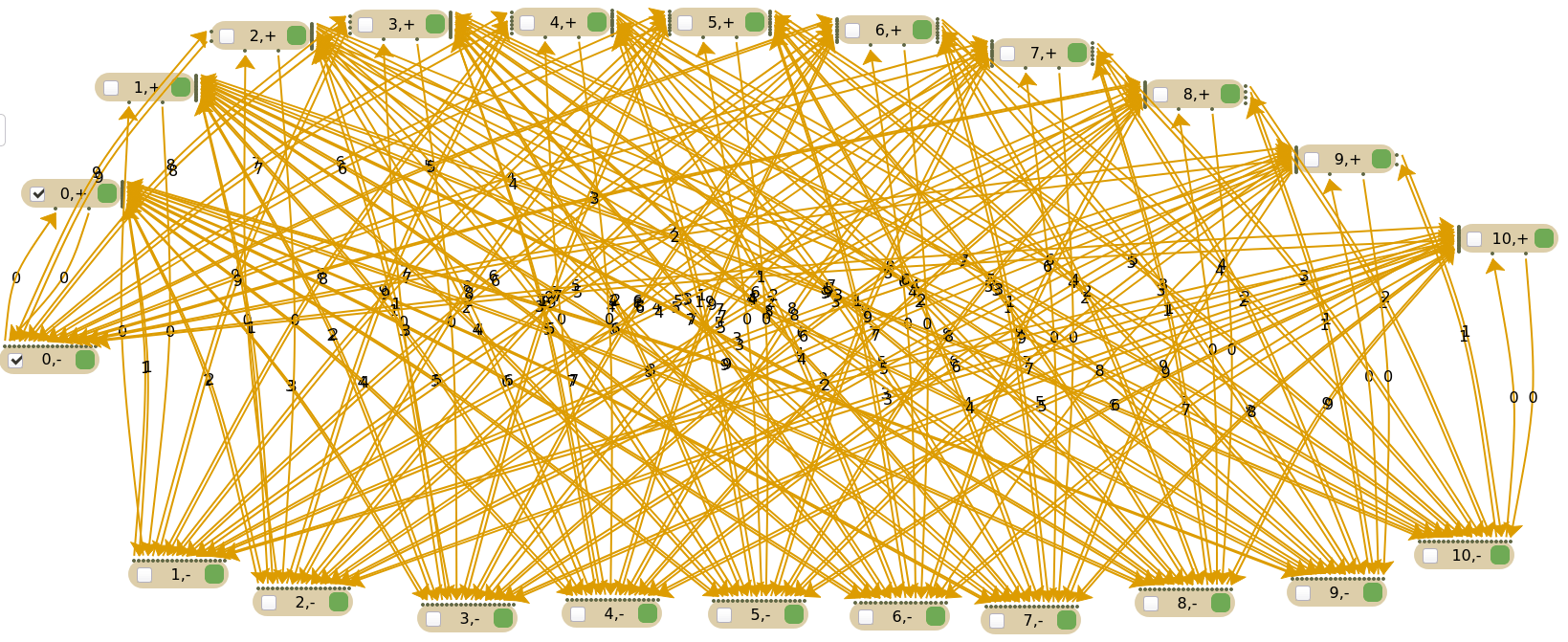
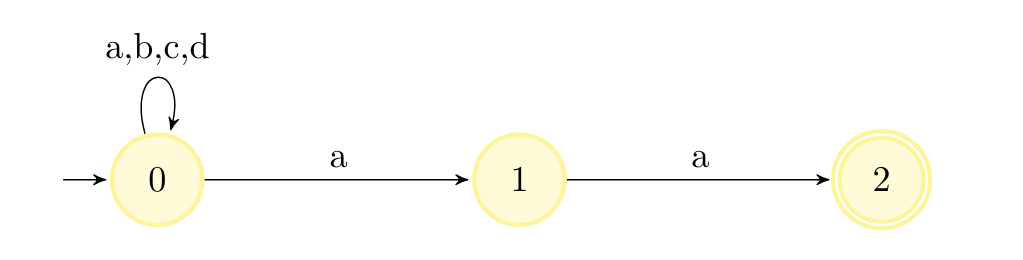
Podúloha c)
Tento receptomat je podobný ako v Podúlohe a), ale akceptujúci stav necyklí pre iné znaky. Receptomat sa tak dostane do akceptujúceho stavu len vtedy, ak sú posledné 2 znaky aa.
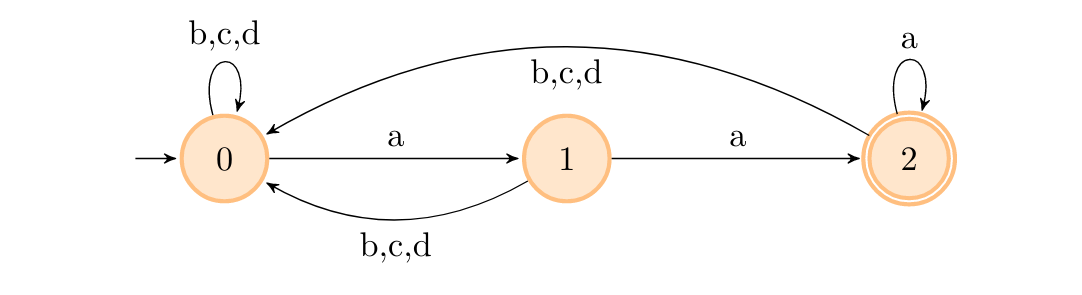
Podúloha d)
Tento receptomat je podobný ako z Podúlohy d) minulého kola, ale potrebujeme aby automat akceptoval len recepty končiace na tento reťazec. Posledný stav teda nebude cykliť pre ľubovoľný prechod ako v podúlohe z minulého kola, ale len pre a. Potom nám stačí spraviť prechody pre nesprávne znaky do počiatočného stavu a pre správne znaky spraviť jednoduchú (lineárnu) cestu.
Podúloha e)
Číslo je deliteľné 25, ak sa končí na 00, 25, 50 alebo 75. Vytvoríme teda receptomat, ktorý bude akceptovať tieto 4 zakončenia (to sú stavy 1, 2, 3 a 4).
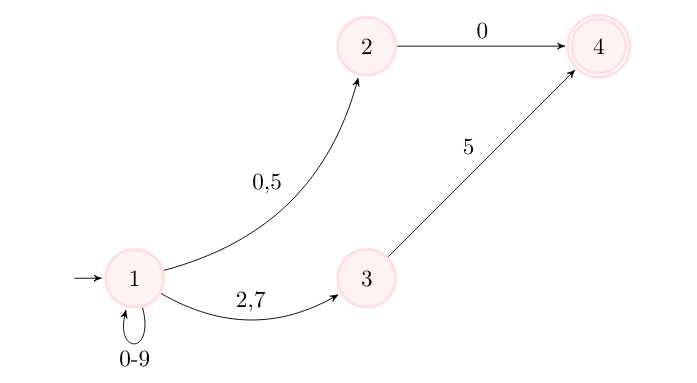
Okrem toho musíme ešte ošetriť prípad 0 (na to si pridáme stav 0).
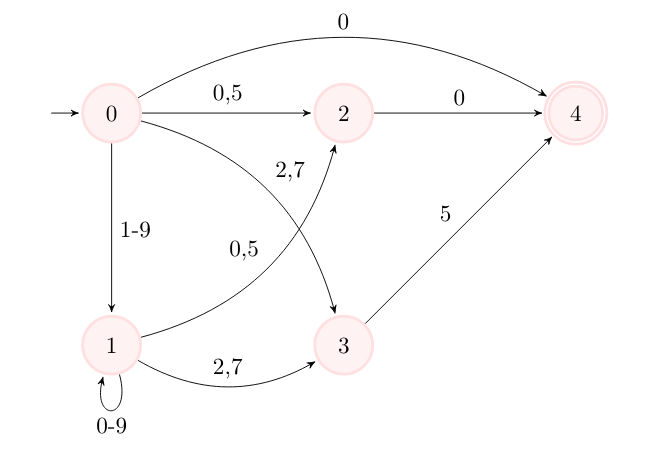
Podúloha f)
Začneme tým, že si ošetríme recept0. Ten je ošetrený stavom 2. Potom si budeme sledovať, či prišli znaky 00, 25, 50 alebo 75 (pomocou stavov 3, 4 a 5). Keď nám v ľubovoľnom stave príde nejaký zo znakov “1,3,4,6,8,9”, vrátime sa do stavu podobnému počiatočnému, ale bez stavu 2 – ten ošetruje len recept 0. V schéme je prechod “2,7” zjednodušený na “b” a “1,3,4,6,8,9” na “a”, “5” a “0” ostávajú nezmenené (čiže napr. “0,a,b” by znamenalo “0,1,2,3,4,6,7,8,9”).
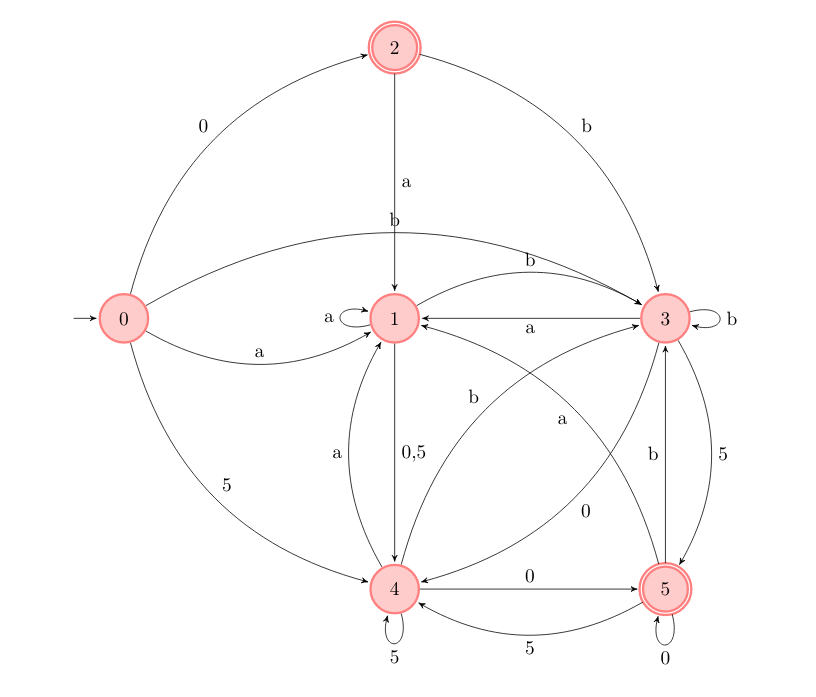
Podúloha g)
Receptomat akceptuje recepty v tvare (a!b!c!d!)*a*, kde výkričník znamená “opakuj tento znak 1 alebo viac krát” a hviezdička znamená “opakuj tento znak 0 alebo viac krát”. Na začiatku teda musíme mať akceptujúci stav, lebo aj prázdny recept je akceptovaný. Ďalej potrebujeme prechod, ktorý nám zaručí aspoň jeden znak a. Následne v našom pôvodnom receptomate len “pootočíme” šípky – tým spôsobíme, že z jednotlivých stavov nepôjdu 2 prechody s rovnakým znakom. Receptomat teda bude deterministický. Nakoniec ešte spravíme aj stav 4 akceptujúci, lebo recept sa nemusí končiť znakom a.
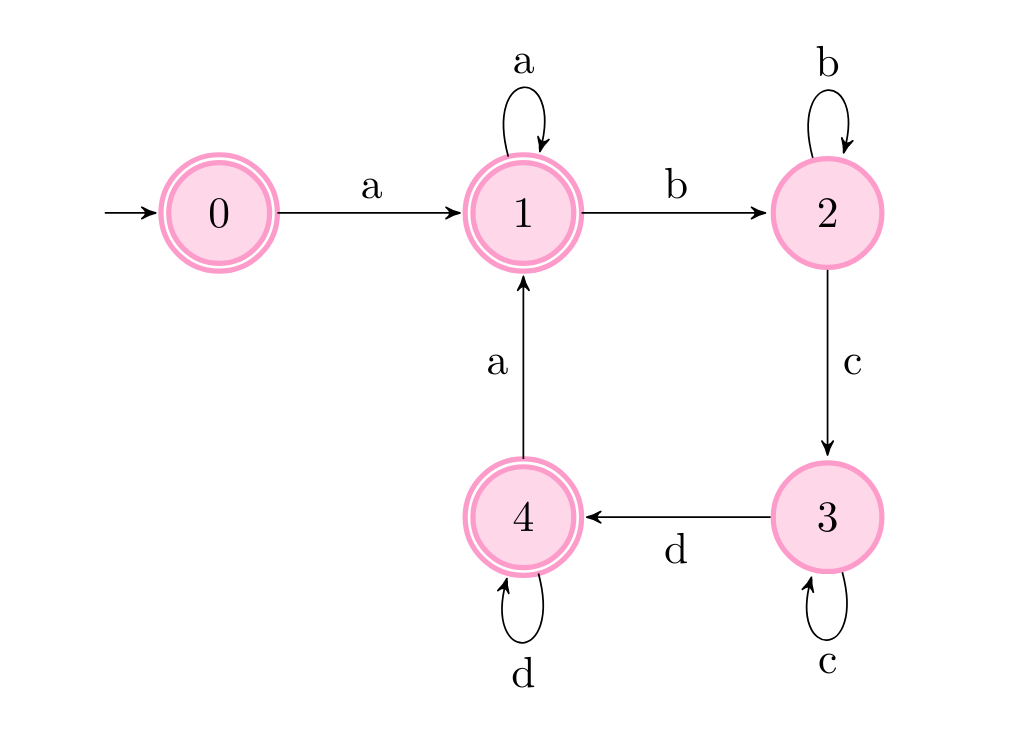
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.