1. Prefixová expedícia vzorové riešenie

Zadanie

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Romanovi na [email protected]

Macín a Ondro sú ostrieľaní lezci a na jar sa rozhodli vyraziť za adrenalínom do Tatier. Pred expedíciou si kúpili turistickú mapu, ktorá vyzerala nasledovne:

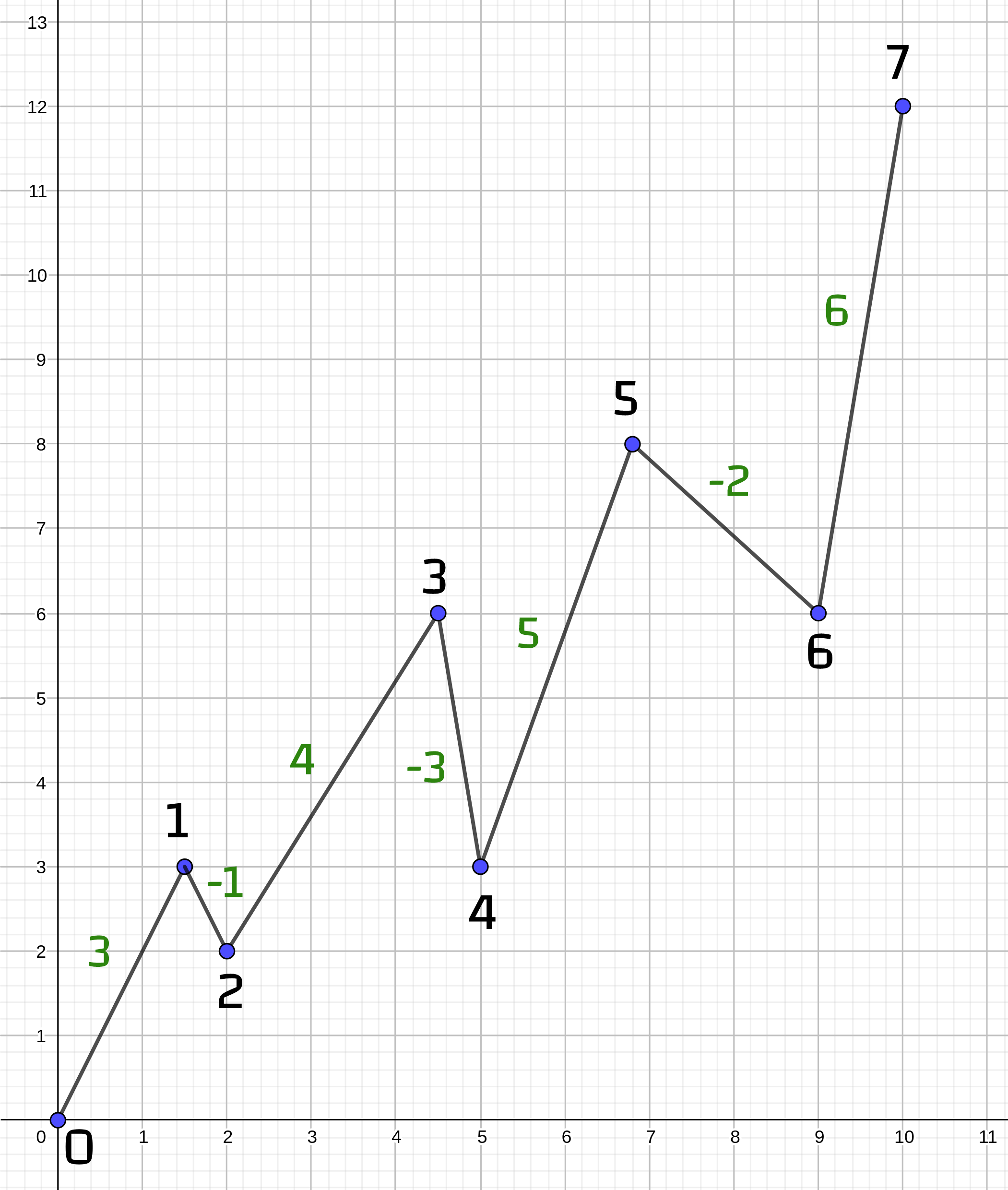
Medzi každými dvoma vrcholmi na mape je jedno číslo, ktoré reprezentuje rozdiel nadmorskej výšky pravého a ľavého vrcholu. Macín s Ondrom sa po mape budú pohybovať zľava doprava. Nevedia však, v ktorom vrchole svoju expedíciu začnú a preto potrebujú pomoc pri výbere trasy.

Úloha

Vrcholy z mapy si očíslujeme zľava doprava \(0\) až \(N\). Údaje o nadmorských výškach budeme reprezentovať pomocou poľa \(A\), ktoré obsahuje jednotlivé rozdiely. Prvok \(A[i]\) obsahuje rozdiel medzi výškou vrchola \(i+1\) a \(i\). Pole \(A\) pre našu mapu vyzerá nasledovne:

Terka chalanom poradila, aby si predpočítali pre pole \(A\) prefixové súčty. Ide o list, na ktorého \(i\)-tej pozícii je súčet všetkých čísel, ktoré sú v pôvodnej postupnosti na pozíciách od \(0\) po \(i - 1\). Pre pole \(A\) bude preto pole \(P\) prefixových súčtov vyzerať nasledovne:

Všimnite si, že tento list je o jedna dlhší ako \(A\) a začína \(0\). Na \(0\)-tej pozícii totiž musí byť súčet čísel od \(0\) po \(−1\), čo je \(0\). Napríklad na \(3\)-tej pozícii je \(6\), pretože súčet prvých \(3\) čísel poľa \(A\) je \(3 - 1 + 4 = 6\).

1. (2 body) Ondru pred cestou zaujíma, kde má mapa svoje stredové vrcholy. Stredový vrchol je taký vrchol, pre ktorý je súčet rozdielov z najľavejšieho vrcholu na mape rovnaký ako súčet rozdielov od najpravejšieho vrcholu na mape. Presnejšie teda hľadáme všetky vrcholy \(k\) také, že \[A[0] + \dots + A[k - 1] = A[k] + \dots + A[N - 1]\] Napríklad na mape zo začiatku zadania sú stredovými vrcholmi vrcholy \(3\) a \(6\). Vymyslite ako efektívne nájsť stredové vrcholy pre pole \(A\). Efektívnym riešením v tomto prípade myslíme také, ktoré pristupuje k jednotlivým prvkov poľa \(A\) a \(P\) čo najmenejkrát. Pošlite nám slovný popis vášho postupu. Váš popis by mal byť zrozumiteľný aj bez znalosti programovania a mal by ho vedieť odsimulovať ktokoľvek s perom a papierom.

2. (2 body) Macín a Ondro plánujú špeciálnu túru, pri ktorej skončia v rovnakej nadmorskej výške, z akej vyrážali. To znamená, že celkový súčet rozdielov nadmorských výšok na trase je rovný \(0\). Viete im poradiť, ako pomocou prefixových súčtov nájsť súvislý úsek v poli \(A\), ktorého súčet je \(0\)? Pri tejto podúlohe neposielajte algoritmus, iba popíšte, ako si v poli prefixových súčtov všimnúť úsek so súčtom \(0\).

3. (3 body) Chalanov pri plánovaní často zaujíma, aký je celkový rozdiel nadmorskej výšky medzi konkrétnymi dvoma vrcholmi. Napríklad pre vrcholy \(2\) a \(5\) je celkový rozdiel \(4 - 3 + 5 = 6\). Všimnite si, že pre vrcholy \(a\) a \(b\) také, že \(a < b\), vieme vypočítať celkový rozdiel ako súčet čiastkových rozdielov, tj. \(A[a] + A[a + 1] + ... + A[b - 1]\). Macín ale stále prichádza s novými nápadmi na trasy a Ondrovi sa už nechce počítať rozdiely prvok po prvku. Musí to ísť predsa lepšie! Vašou úlohou je preto prísť na to, ako šikovne spočítať celkový rozdiel medzi výškami vrcholov \(a\) a \(b\) pomocou poľa prefixových súčtov \(P\).

4. (3 body) Ako pre pole \(A\) vytvoriť pole prefixových súčtov \(P\)? Podobne ako v podúlohe a) vymyslite efektívne riešenie, teda také, ktoré k prvkom poľa \(A\) a \(P\) prístupi čo najmenejkrát, a pošlite nám jeho slovný popis.

5. (5 bodov) Telo sa musí vyššej nadmorskej výške vždy prispôsobiť. Výstupiť preto za jeden deň oveľa vyššie a prenocovať tam by mohlo byť nebezpečné. Chalani si určili výšku \(k\), o ktorú chcú za jeden deň vystúpiť vyššie. Vašou úlohou bude nájsť všetky dvojice vrcholov, medzi ktorými je celkový rozdiel nadmorských výšok práve \(k\). Napríklad na našej mape by pre \(k = 4\) splňovali túto podmienku dvojice vrcholov \((2, 3)\) a \((2, 6)\). Opäť nám pošlite slovný popis čo najefektívnejšieho riešenia.

Ak viete programovať, niektoré z podúloh si môžete vyskúšať naprogramovať a poslať nám vaše kódy. Nedostanete síce body naviac, ale vaše programy okomentujeme a poradíme vám, čo by sa dalo spraviť lepšie alebo krajšie. Pri programátorských úlohách vám nedávame spätnú väzbu k vašim programom, preto máte teraz jedinečnú šancu.

P.S.: Ondro s Macínom a kamarátmi Tatry skutočne navštívili. Ako sa Čechom v Tatrách darilo a či ich zachraňovala horská služba, sa dozviete v článku od Ondru.

Táto úloha bola venovaná prefixovým súčtom, ktoré sú neoddeliteľnou súčasťou výbavy programátora. Pochopenie vzorového riešenia vám určite pomôže pri riešení mnohých úloh v budúcnosti.

Podúloha A

Vašou úlohou bolo nájsť všetky vrcholy \(k\) také, že \[A[0] + \dots + A[k - 1] = A[k] + \dots + A[N - 1]\] V zadaní bolo spomenuté, že pole prefixových súčtov \(P\) obsahuje na \(i\)-tej pozícii súčet všetkých čísel, ktoré sú v pôvodnej postupnosti na pozíciách od \(0\) po \(i - 1\). To je vlastne prvý súčet z rovnosti vyššie. Teda pre každý vrchol \(k\) platí, že \[P[k] = A[0] + \dots + A[k - 1]\] Napríklad pre vrchol \(4\) je súčet \(A[0] + A[1] + A[2] + A[3]\) rovný \(3\), a preto aj hodnota \(P[4]\) je \(3\).

Všimnite si, že súčet na druhej strane rovnosti, \(A[k] + \dots + A[N - 1]\), je rovný celkovému súčtu prvkov poľa \(A\) bez ľavej strany z pôvodnej rovnosti. Formálne \[A[k] + \dots + A[N - 1] = (A[0] + \dots + A[N - 1]) - (A[0] + \dots + A[k - 1])\] Posledné pozorovanie je, že celkový súčet poľa \(A\) nájdeme v poli prefixových súčtov na poslednom, \(N\)-tom mieste.

Aby \(k\) bolo stredovým vrcholom, musí preto platiť \[P[k] = P[N] - P[k]\]

Pri riešení teda stačí prejsť v jednom cykle postupne všetky možné \(k\), a pri každom overiť podmienku uvedenú vyššie.

pre k := 0 do N:
    ak (P[k] == P[N] - P[k]):
        vypis(k + ' je stredovy vrchol')

Pri každom vrchole sa pozrieme na 3 hodnoty poľa \(P[]\), spravíme jedno porovnanie a prípade niečo vypíšeme. Celkovo teda pre jeden vrchol vykonáme konštantne veľa operácii. To znamená, že počet operácií pre jeden vrchol nezávisí od vstupných hodnôt, napríklad od hodnoty \(N\). Vrcholov máme \(N + 1\), takže program vykoná \(3 \cdot (N + 1)\) prístupov k prvkom poľa \(P\). To je lineárne veľa v závislosti od \(N\), a preto má naše riešenie časovú zložitosť \(O(N)\). Uvedomte si, že rýchlejšie riešenie nevymyslíme, pretože v najhoršom prípade by každý z vrcholov bol stredový (samé hodnoty 0) a v takom prípade by sme museli vypísať všetkých \(N + 1\) vrcholov. Operácia vypísania \(N + 1\) prvkov má zložitosť \(O(N)\), takže aj keby sme našli všetky stredové vrcholy rýchlejšie ako v \(O(N)\), ich výpis nám zaberie \(O(N)\) operácii.

Podúloha B

Kedy je úsek medzi dvoma vrcholmi \(a\) a \(b\) (\(a < b\)) rovný \(0\)? V zadanej úlohe túto podmienku spĺňajú napr. vrcholy \(1\) a \(4\) a tiež \(34\) a \(6\). Zjavne musí platiť \[A[a] + A[a + 1] + \dots + A[b - 1] = 0\] Súčet na ľavej strane môžeme dostať aj tak, že odčítáme súčet prvkov po \(A[a - 1]\) od súčtu po \(A[b - 1]\). Teda \[A[a] + A[a + 1] + \dots + A[b - 1] = (A[0] + \dots + A[b - 1]) - (A[0] + \dots + A[a - 1])\] Na pravej strane dostávame prefixové súčty \(P[b]\) a \(P[a]\) takže skrátene \[A[a] + A[a + 1] + \dots + A[b - 1] = P[b] - P[a]\] Tu zároveň dostávame riešenie nasledujúcej podúlohy, ktorá sa pýta, ako vypočítať súčet úseku od \(a\) po \(b - 1\). Pokračujme ale ďalej. My teraz chceme, aby bol súčet medzi \(a\) a \(b\) rovný \(0\). Preto môžeme do rovnice vyššie namiesto všeobecného súčtu napísať práve \(0\), ktorú chceme dostať. \[0 = P[b] - P[a]\] Odtiaľ vidíme, že tento prípad nastane práve vtedy, keď \(P[a] = P[b]\). Preto môžeme povedať, že súčet medzi vrcholmi \(a\) a \(b\) je rovný \(0\) ak sa prefixové súčty \(P[a]\) a \(P[b]\) rovnajú.

Podúloha C

Ako bolo avizované v predošlom riešení, súčet \(A[a] + A[a + 1] + \dots + A[b - 1]\) pre \(a < b\) vieme získať pomocou prefixových súčtov ako rozdiel \(P[b]\) a \(P[a]\). \[A[a] + A[a + 1] + \dots + A[b - 1] = P[b] - P[a]\] Ak už máme vypočítané prefixové súčty, stačí nám jediná aritmetická operácia na vypočítanie celého súčtu úseku. Namiesto postupného pričítavania hodnôt medzi \(a\) a \(b-1\), ktorých by mohlo byť až \(N\) máme zakaždým zaručené iba jedno odčítanie. Takéto riešenie je teda oveľa rýchlejšie.

Podúloha D

Ako prvé riešenie by nám mohlo napadnúť \(i\)-tu pozíciu \(P\) spočítať tak, že spočítame všetky prvky od \(0\) po \(i - 1\), teda

pre i := 0 do N:
    sucet := 0
    pre j := 0 do i - 1:
        sucet := sucet + A[j]

    P[i] := sucet

Toto je korektné riešenie, ale zbytočne pomalé. V našom programe \(P[i]\) počítame tak, že sčítame postupne všetky prvky \(A[0], \dots, A[i - 1]\). Potom pre \(i + 1\) znovu sčítavame postupne \(A[0], \dots, A[i - 1], A[i]\). Všimnite si, že medzi členmi \(i\) a \(i + 1\) poľa \(P\) nie je veľký rozdiel, konkrétne \(P[i + 1]\) obsahuje oproti \(P[i]\) hodnotu \(A[i]\) navyše. Veľa roboty tak robíme opakovane. Tento fakt vieme využiť nasledovne:

P[0] := 0
pre i := 0 do N - 1:
    P[i + 1] := P[i] + A[i]

Je jasné, že druhé riešenie je výrazne rýchlejšie, prvý cyklus je totiž rovnaký, v prvom v prípade sa v ňom však opakujeme, v druhom už nie. Toto zlepšenie je však výrazné aj v časovej zložitosti. Keď sa pozrieme na počet sčítaní, ktoré musíme spraviť, v prvom prípade to bude

\[1 + 2 + 3 + \dots + N = \frac{N(N+1)}{2}\]

, pretože v prvom opakovaní spravíme jedno sčítanie, v druhom dve, atď¹. Takýto počet operácií potom zaokrúhlime na \(N^2\) a povieme, že časová zložitosť je \(O(N^2)\).

Druhé riešenie však spraví iba \(N\) sčítaní a jeho časová zložiosť je preto iba \(O(N)\), čo je opäť raz optimálne, keďže hodnoty poľa \(A\) musíme v čase \(O(N)\) načítať.

Podúloha E

Táto podúloha má aj svoju ťažšiu verziu. Jej zadanie nájdeš na konci vzoráku.

V tejto podúlohe bolo vašou úlohou vypísať všetky dvojice \((a, b)\), pre ktoré platí \(P[b] - P[a] = k\). Nasledujúce riešenie prejde v cykle všetky dvojice \((i, j)\) také, že \(i < j\) a overí podmienku zo zadania.

pre i := 0 do N:
    pre j := i + 1 do N:
        ak (P[j] - P[i] == k):
            vypis(i + ' ' + j)

Všetkých dvojíc je spolu \(\frac{N(N + 1)}{2}\). Prečo? Predstavte si, že pre vrchol \(0\) vyberáme druhý vrchol do dvojice. Máme \(N\) možností (\(1, 2, \dots, N\)). Ak pre vrchol \(1\) vyberáme druhý vrchol do dvojice, máme \(N - 1\) možnosti (\(2, 3, \dots, N\)). Ak by sme takto pokračovali ďalej, dostaneme spolu počet všetkých dvojíc \[N + (N - 1) + \dots + 2 + 1 + 0\] Ak tento súčet otočíme, je to opäť súčet prvých \(N\) prirodzených čísel, s ktorým sme sa už stretli v podúlohe D. V poznámke pod vzorákom sa dozviete prečo sa tento súčet rovná \(\frac{N(N + 1)}{2}\).

V podúlohe D sme tiež zistili, že tento počet rastie kvadraticky v závislosti na \(N\). To znamená, že naše riešenie má kvadratickú časovú zložitosť \(O(N^2)\), pretože každú dvojicu prejde práve raz a spraví pre ňu konštantne veľa operácií (pristúpi k \(2\) prvkom poľa \(P\), vyhodnotí podmienku a prípadne vypíše hlášku na výstup). Uvedomte si, že lepšie riešenie nevymyslíme, pretože v najhoršom prípade by každá z dvojíc vrcholov mohla mať medzi sebou rozdiel \(k\) a všetky by sme ich tak museli vypísať.

Ťažšia verzia tejto úlohy sa nepýta na všetky dvojice s rozdielom \(k\), ale iba na ich počet. Výstupom tak bude už iba jedno číslo, čiže časová zložitosť riešenia nie je limitovaná veľkosťou výstupu ako v pôvodnej podúlohe. Prídete na to ako efektívne vyriešiť túto úlohu?