Zadanie
Ak nevieš programovať, nezúfaj! Môžeš sa to naučiť a ešte za to získať body, ktoré sa ti budú počítať namiesto tejto úlohy.
Stačí, že pôjdeš na stránku Programátorskej Liahni (liahen.ksp.sk). Keď budeš riešiť sadu variables_cpp, bodmi, ktoré získaš si môžeš nahradiť riešenie tejto úlohy. Stačí ak na spodku tejto stránky odovzdáš pdf-ko s prezývkou, ktorú používaš na Liahni.
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Romanovi na [email protected]
Prišli prázdniny a Bonifác sa nudil. Všetko sa ale zmenilo, keď na záchode otvoril časopis a na poslednej strane objavil maľovanú krížovku. Na nasledujúcom obrázku je jej zadanie aj s Bonifácovým riešením:
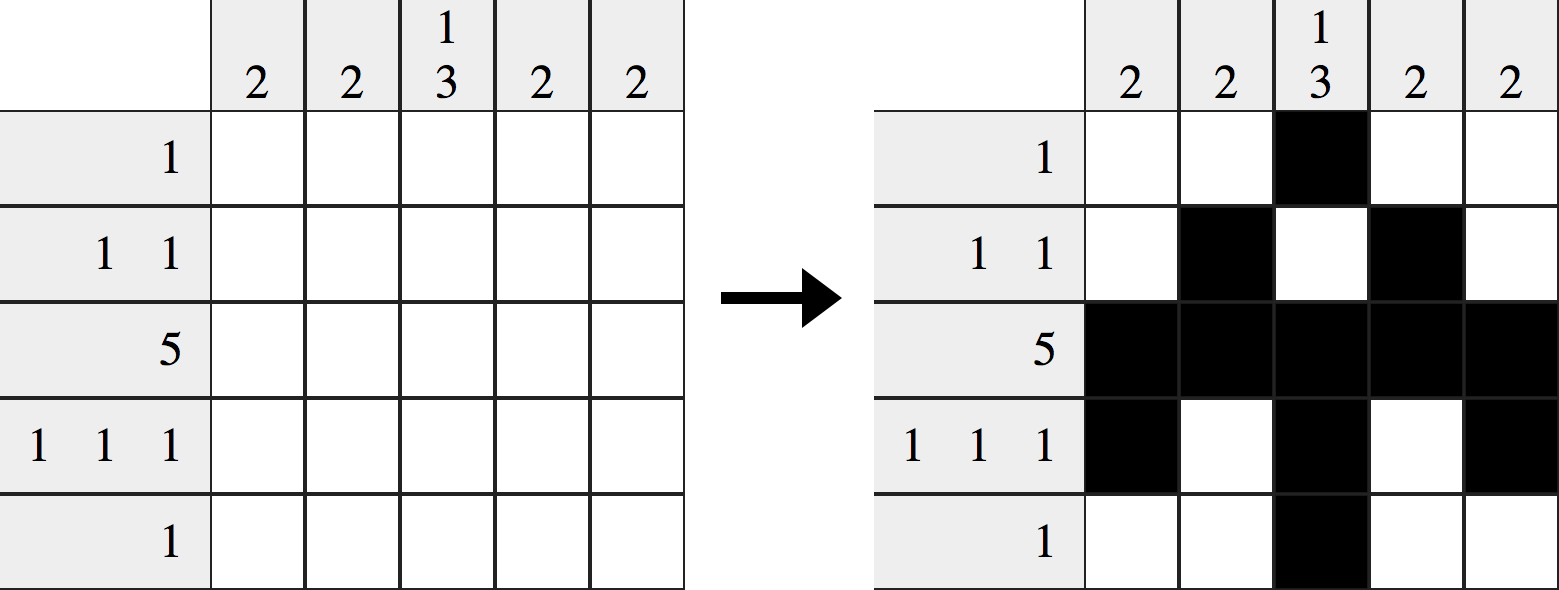
Skúste si všimnúť závislosť medzi číslami na okrajoch a výsledným obrázkom – v každom riadku je presne toľko vyfarbených úsekov (súvislých čiernych políčok), koľko je pre daný riadok za okrajom nápovedných čísel. Tieto čísla zároveň presne určujú, koľko bude daný úsek obsahovať vyfarbených políčok a tiež poradie týchto úsekov. Táto vlastnosť platí rovnako aj pre stĺpce1.
Bonifác rýchlo prišiel na to, ako maľované krížovky riešiť, netrvalo preto dlho a vyriešil všetky, ktoré doma našiel. Teraz však potrebuje nové krížovky, pretože inak ho znovu pochytí hrozná nuda. Jeho sestra Amálka je maliarka a tak sa rozhodla, že pre Bonifáca namaľuje nové obrázky. Celý deň pilne kreslila a podarilo sa jej vytvoriť slona, stoličku, vlak či korytnačku. Z jej obrázkov je ale potrebné ešte vytvoriť zadanie maľovaných krížoviek pre Bonifáca. S touto úlohou si už nevie dať rady a tak potrebuje vašu pomoc.
Na jednom z Amálkiných obrázkov si teda ukážeme, čo bude vašou úlohou.
Úloha

Ako by vyzeralo zadanie maľovanej krížovky pre tento obrázok? Potrebujeme popísať súvislé úseky v jednotlivých riadkoch a stĺpcoch. Začneme riadkami – v prvom riadku je iba jeden úsek veľkosti \(2\). Nasleduje riadok, ktorý by sme popísali nápovedou \(2\), \(4\), pretože prvý úsek v ňom má veľkosť 2 a druhý veľkosť 4. Analogicky postupujeme pre ostatné riadky.
Pre stĺpce postupujeme rovnako – v prvom stĺpci je iba jeden úsek veľkosti \(2\), v druhom stĺpci jeden úsek veľkosti \(3\), atď..
Na vstupe máme Amálkin čiernobiely obrázok, ktorý má \(r\) riadkov a \(s\) stĺpcov. Obrázok je mriežka s rozmermi \(r \times s\), ktorá obsahuje \(1\) na pozíciach, ktoré sú vyfarbené, teda čierne a \(0\) na nevyfarbených, bielych políčkach. Vašou úlohou je z tohto obrázka vytvoriť zadanie pre maľovanú krížovku, teda spočítať súvislé úseky vyfarbených políčok v jednotlivých riadkoch a stĺpcoch.
Formát vstupu
Na prvom riadku dostanete dve čísla \(r\) a \(s\) – počet riadkov a stĺpcov obrázka. Nasleduje popis obrázka. Na každom z nasledujúcich \(r\) riadkov sa bude nachádzať \(s\) medzerou oddelených čísel. Číslo je buď \(1\) alebo \(0\), podľa toho, či je dané políčko čierne alebo biele.
Formát výstupu
Ako prvé budeme vypisovať úseky v riadkoch maľovanej krížovky. Pre každý z \(r\) riadkov obrázka, začínajúc najvrchnejším, vypíšte na samostatnom riadku medzerami oddelené veľkosti jednotlivých úsekov v danom riadku v poradí zľava doprava. Ak sa v tomto riadku žiaden úsek nenachádza, vypíšte 0.
Hneď za popisom riadkov bude nasledovať práve jeden prázdny riadok. Potom nasleduje popis stĺpcov. Ten bude rovnaký ako pri riadkoch – pre každý z \(s\) stĺpcov, začínajúc najľavším, vypíšte na samostatnom riadku medzerami oddelené veľkosti jednotlivých úsekov v danom stĺpci v poradí zhora nadol. Ak v stĺpci nie je žiadny vyfarbený úsek, vypíšte 0.
Hodnotenie
Pri testovaní bude vaše riešenie spustené na rôznych sadách vstupov, ktoré sa navzájom líšia obtiažnosťou ich riešenia. Za každú úspešne vyriešenú sadu dostanete 3 body. Obmedzenia pre \(r\) a \(s\) nájdete v nasledujúcej tabuľke.
| Číslo sady | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| maximálne \(r\) | \(1\) | \(1\,000\) | \(20\) | \(200\) | \(1\,000\) |
| maximálne \(s\) | \(1\,000\) | \(1\) | \(20\) | \(200\) | \(1\,000\) |
Príklady
Input:
6 10
0 0 0 0 0 1 1 0 0 0
1 1 0 0 1 1 1 1 0 0
1 1 0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 0
0 0 0 1 0 0 0 1 0 0
0 0 1 1 0 0 1 1 0 0Output:
2
2 4
2 6
8
1 1
2 2
2
3
1 1
4
3
4
4 1
5
2
0Vstup je Amálkin obrázok, ktorý sme si ukázali vyššie. Vo výstupe je 7. riadok prázdny – oddeľuje popis riadkov a stĺpcov. Posledný stĺpec obrázka je nevyfarbený, čomu vo výstupe zodpovedá 0 na konci.
Input:
1 8
1 0 1 1 1 0 1 1Output:
1 3 2
1
0
1
1
1
0
1
1Vstup, ktorý sa môže vyskytnúť v prvej sade.
Vyriešiť maľovanú krížovku si môžete vyskúšať aj vy, nepotrebujete k tomu ani časopis, existuje mnoho webových stránok s týmto hlavolamom.↩
Myšlienka
Máme obrázok o veľkosti \(r \times s\), v ktorom chceme nájsť dĺžky súvislých úsekov čiernych políčok v riadkoch aj stĺpcoch. Ako prvé si musíme tento obrázok uložiť do pamäte počítača. To však nie je problém, práve na to sú určené dvojrozmerné polia. Dvojrozmerné pole si môžete predstaviť ako tabuľku, v ktorej je každé políčko označené číslom riadka a stĺpca. Jediné na čo si dajte pozor je, že v informatike číslujeme od 0.
Začnime tým, že si vysvetlíme, ako vypočítať výsledok pre jeden riadok. Riadok budeme prechádzať postupne zľava doprava. Naviac budeme mať jednu premennú ans, v ktorej si budeme pamätať, aký dlhý úsek čiernych políčok (jednotiek) máme aktuálne prečítaný. Predstavme si, že ideme spracovávať ďalšie políčko v riadku. Ak je na tomto políčku 1, znamená to, že aktuálny úsek jednotiek má byť o jedna dlhší. Preto zväčšíme hodnotu v našej premennej: ans = ans + 1.
Naopak, ak je na tomto políčku 0, úsek jednotiek na ňom končí. Pozrieme sa teda, aká hodnota je v premennej ans. Ak je táto hodnota nenulová, skutočne tu končí nejaký úsek jednotiek a jeho dĺžku (obsah premennej ans) by sme mali vypísať. Následne hodnotu ans vynulujeme, lebo aktuálne nemáme prečítané žiadne za sebou idúce jednotky, a pokračujeme v spracovávaní riadka.
Pozor si musíme dať v dvoch prípadoch. Ak riadok končí 1, tak posledný úsek si nikdy nepoznačíme, lebo niečo také by sme spravili až keby sme narazili na ďalšiu 0 v danom riadku, žiadna v ňom však už nie je. Po spracovaní celého riadku sa preto treba ešte raz pozrieť na to, či v premennej ans nie je nenulová hodnota – nejaký zabudnutý úsek. Druhý špeciálny prípad je, ak v riadku nie je žiadna 1, vtedy si musíme dať pozor, aby sme vypísali požadovanú 0.
No a nie je ťažké si uvedomiť, že spracovanie stĺpcov je veľmi podobné. Jediný rozdiel pri našom algoritme bude v tom, že načítaný obrázok neprechádzame po riadkoch, ale po stĺpcoch. Všetko ostatné ostane rovnaké.
Časová a pamäťová zložitosť
Aká bude časová zložitosť tohto riešenia? Celý obrázok musíme prejsť dvakrát – raz po riadkoch a raz po stĺpcoch. To nás stojí \(O(r\cdot s)\) operácií, pretože na každom z \(r \times s\) políčok strávime iba konštantne veľa času – upravíme premennú ans. Nemôžeme ešte zabudnúť do časovej zložitosti započítať načítavanie obrázka a výpis úsekov. Stačí si ale uvedomiť, že celkový počet úsekov je zhora obmedzený veľkosťou obrázka. Preto výsledná časová zložitosť ostane \(O(r \cdot s)\).
Pamäťová zložitosť je tiež \(O(r \cdot s)\), pretože si celý obrázok musíme uložiť niekam do pamäte. Ak by sme ale nemuseli počítať úseky v stĺpcoch, ale iba v riadkoch, vedeli by sme dosiahnuť pamäťovú zložitosť \(O(1)\). Na riešenie by nám teda stačilo iba niekoľko premenných. Viete prísť na to, ako by sme to robili?
#include <bits/stdc++.h>
using namespace std;
inline void vypis(const vector<int> &useky) {
if (useky.empty()) { // v riadku/stlpci sa nenachadzaju ziadne useky
cout << "0\n";
return;
}
for(int i = 0; i < useky.size(); ++i) {
if (i > 0)
cout << " ";
cout << useky[i];
}
cout << "\n";
}
int main() {
int r, s;
cin >> r >> s;
vector<vector<int> > obrazok(r, vector<int>(s));
// nacitanie obrazku
for(int i = 0; i < r; ++i) {
for(int j = 0; j < s; ++j) {
cin >> obrazok[i][j];
}
}
vector<int> useky;
int ans;
// spracovanie riadkov
for(int i = 0; i < r; ++i) {
ans = 0;
for(int j = 0; j < s; ++j) {
if (obrazok[i][j] == 1) { // usek mozeme predlzit
ans++;
} else { // narazili sme na cierne policko, takze tu konci usek dlzky ans
// musime osetrit pripad, kedy ma usek dlzku 0 (napr. ak nasleduju
// dve cierne policka za sebou
if (ans > 0) {
useky.push_back(ans);
ans = 0;
}
}
}
// riadok mohol skoncit 1 (bielym polickom), takze posledny usek
// musime pridat zvlast
if (ans > 0)
useky.push_back(ans);
vypis(useky);
useky.clear(); // vymazanie pola useky
}
cout << "\n";
// spracovanie stlpcov je velmi podobne spracovaniu riadkov,
// rozdiel je v tom, ze obrazok prechadzame po stlpcoch, takze
// sa nam zmenia medze for-cyklov a
for(int j = 0; j < s; ++j) { // pre kazdy stlpec
ans = 0;
for(int i = 0; i < r; ++i) { // pre kazdy riadok v stlpci
if(obrazok[i][j] == 1) {
ans++;
} else {
if(ans > 0) {
useky.push_back(ans);
ans = 0;
}
}
}
if (ans > 0)
useky.push_back(ans);
vypis(useky);
useky.clear();
}
return 0;
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.