Zadanie
Ak máte akékoľvek otázky ohľadom tejto úlohy napíšte Maji Vajdovej na
V jednom malom neznámom cirkuse na okraji jedného malého bezvýznamneho mesta sa jedného nudného dňa premnožili blchy. Celý cirkus sa obrátil hore nohami. Namiesto toho, aby sa nacvičovali nové čísla, zvieratá aj ľuďia začali splašene pobehovať po okolí a pomaly cirkus opúšťať. Keď to už vyzeralo tak, že malý neznámy cirkus bude treba zavrieť, blchy zmutovali do obrovských rozmerov.
To, čo sa na prvý pohľad javilo ako ešte väčšia katastrofa, sa nakoniec ukázalo ako výhoda, ktorá náš malý cirkus preslávila po celom svete. Také veľké blchy sa totiž dajú trénovať, preto sa náš cirkus premenoval na blší a funguje dodnes.
Pred blším vystúpením sa vždy na podlahu nakreslí niekoľko kruhov a očíslujú sa začínajúc od \(1\). Do každého sa potom položí jedna blcha. Vždy, keď počas vystúpenia cvičiteľ zapíska na píšťaľku, všetky blchy skočia zo svojho kruhu do nejakého (nie nutne iného) určeného kruhu. Kruh, do ktorého má blcha skočiť je určený číslom kruhu, v ktorom blcha stojí. Napríklad môže byť povedané, že z kruhu \(3\) sa skáče do kruhu \(1\) a z kruhu \(2\) sa skáče späť do kruhu \(2\). Toto určenie sa počas celého vystúpenia nemení.
Cvičitelia by však potrebovali pomôcť s plánovaním nových choreografií a s prosbou o pomoc sa obrátili na vás.
Úloha
Máme choreografiu pozostávajúcu z \(n\) kruhov pre blchy a z \(n\) bĺch. Pre každý kruh je určené, do ktorého kruhu sa z neho blcha musí pri zapískaní pohnúť. Na obrázku je vidno rozostavenie pre 5 bĺch. Šípka vedúca z kruhu určuje, do ktorého kruhu má z neho blcha skočiť.
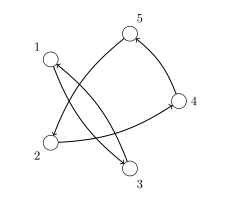
Na ďalšom obrázku je vidno inú choreografiu pre \(5\) bĺch. Môžete si na nej všimnúť, že po dvoch zapískaniach sa všetky blchy ocitnú v kruhu \(2\). Takéto blšie choreografie voláme stretávacie. Aj blšia choreografia na predchádzajúcom obrázku má zaujímavú vlastnosť: po presne šiestich zapískaniach bude každá blška naspäť v krúžku, v ktorom bola na začiatku vystúpenia. Takéto blšie choreografie voláme opakovacie.
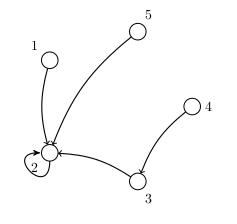
Vašou úlohou je vymyslieť niekoľko choreografií tak, aby spĺňali nasledovné požiadavky. Vo vašom riešení však nestačí nakresliť žiadanú choreografiu, ale aj vysvetliť, prečo má daná choreografia požadované vlastnosti. Choreografie bez popisu budú hodnotené najviac polovicou bodov.
(1 bod) Nakreslite opakovaciu choreografiu, pre ktorú sa blšky na pôvodné miesta vrátia nie po \(6\), ale po \(7\) skokoch. Môžete použiť ľubovoľný počet krúžkov, nemusí ich byť len \(5\).
(1 bod) Nakreslite opakovaciu choreografiu, v ktorej sa blšky na pôvodné miesta vrátia prvýkrát až po \(10\) skokoch. Tentokrát ale musíte použiť menej ako \(10\) krúžkov.
(2 body) Choreograf by od vás chcel blšiu choreografiu s \(10\) krúžkami. Zaujímalo by ho, aké je najväčšie číslo \(k\), pre ktoré platí, že sa blšky prvýkrát ocitnú všetky naraz vo svojich počiatočných pozíciach po práve \(k\) zapískaniach. Ako taká choreografia vyzerá? Prečo ja vami nájdené \(k\) najväčšie možné?
(2 body) Nájdite choroegrafiu s čo najmenej krúžkami, ktorá sa prvýkrát opakuje po \(3960\) zapískaniach.
(4 body) Nájdite najmenší počet krúžkov pre choreografiu, ktorá sa má prvýkrát opakovať po \(n\) zapískaniach. Vo vašom riešení popíšte postup ako takúto choreografiu nakresliť a vysvetlite, prečo sa neoplatí kresliť túto choreografiu inak. Dbajte na správnosť vašich tvrdení a argumentov.
(1 bod) Skúste vymyslieť choreografiu, ktorá nebude ani stretávacia, ani opakovacia.
(1 bod) Janko si nakreslil choreografiu so \(47\) krúžkami. Neukázal ju Marienke, len jej povedal, že jeho choreografia je stretávacia. Na to Marienka povedala: “Nemusíš mi ju ukazovať. Napriek tomu som si istá, že keď \(b\)-krát zapískam, budú už všetky blšky v tom istom krúžku.” Pre aké najmenšie \(b\) má Marienka pravdu bez ohľadu na to, ako vyzerá Jankova choreografia? Prečo?
(3 body) V stretávacej choreografii z príkladu si môžeme všimnúť šipku vedúcu z krúžku 2 naspäť do krúžku 2. Takúto šipku voláme slučka. Existuje stretávacia choreografia, v ktorej nie sú žiadne slučky? Svoju odpoveď zdôvodnite.
Táto úloha vyzerá ako úloha o kreslení obrázkov, ale nakoniec sa ukáže, že je to celé o niečom inom…
Podúloha a)
Najjednoduchšie riešenie je kruh so \(7\) blchami ako na obrázku.
Je zjavné, že každá blcha musí prejsť celý kruh, kým sa vráti na svoje pôvodné miesto a bude jej to trvať presne \(7\) krokov. Situácia je pre každú blšku úplne rovnaká, takže po siedmych krokoch budú všetky blchy súčasne na svojich pôvodných miestach.
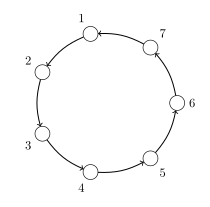
Takýto obrázok budeme volať cyklus dĺžky \(7\). V ďalších podúlohách budeme používať cykly rôznych dĺžok.
Podúloha b)
Po chvíľke kreslenia môžeme prísť na to, že funguje choreografia pozostávajúca z dvoch cyklov, jedného dĺžky \(5\) a druhého dĺžky \(2\). Ale prečo je to tak? Blšky, ktoré sú súčasťou cyklu dĺžky \(2\) sa na svoje miesto vrátia po \(2, 4, 6, 8, 10 \dots\) krokoch (zakaždým musia prejsť celým kruhom dĺžky \(2\)). Je jasné, že sú to všetko násobky dvojky.
Takéto tvrdenie si môžeme zovšeobecniť. Blcha v cykle dĺžky \(n\) sa na svoje miesto vráti každých \(n\) krokov, teda vždy, keď je počet krokov od začiatku násobok čísla \(n\). Blška, ktorá je súčasťou cyklu dĺžky \(5\) sa teda na svoje miesto vráti po \(5, 10, 15\)… krokoch. Tým pádom sa blšky v oboch cykloch prvýkrát naraz vrátia na svoje miesta po 10 krokoch.

Podúloha c)
V tejto podúlohde hľadáme opakovaciu choreografiu, ktorá obsahuje 10 blšiek. Bolo by preto na mieste sa zamyslieť, ako môžu vyzerať opakovacie choreografie. Z každého krúžka, ktorý predstavuje začiatočnú pozíciu nejakej blšky, vychádza jedna šípka do iného (alebo aj toho istého) krúžka. To znamená, že ak máme \(n\) krúžkov, bude medzi nimi viesť aj \(n\) šípiek. Uvedomme si teraz, že do každého krúžku musí viesť práve jedna šípka.
Ak by do nejakého krúžku neviedla žiadna šípka, blška, ktorá začína v tomto krúžku sa sem nikdy nevie vrátiť, lebo nemá ako. Takáto choreografia by teda nebola opakovacia. A ak máme \(n\) krúžkov a \(n\) šípiek a do každého krúžku musí viesť aspoň jedna šípka, neostáva nám iná možnosť, ako že do každého krúžku vedie práve jedna šípka. A naozaj, jediné obrázky, ktoré vieme nakresliť dodržiac toto pravidlo sú cykly rôznych dĺžok. Každá opakovacia choreografia sa teda skladá z niekoľkých (možno rôzne dlhých) cyklov.
V podúlohe b) sme videli, že choreografia z dvoch cyklov dĺžok 2 a 5 sa prvýkrát zopakuje po 10 krokoch. To je totiž najmenšie číslo, ktoré je zároveň násobkom čísla 2 aj čísla 5. Inými slovami, 10 je najmenším spoločným násobkom týchto dvoch čísel. Uvedomme si, že toto platí aj všeobecne. Ak budeme mať niekoľko cyklov, tak sa všetky blšky prvýkrát naraz vrátia na svoje pôvodné miesto po najmenšom spoločnom násobku ich dĺžok, lebo to je prvé číslo, ktoré je násobkom dĺžok všetkých cyklov.
Ak teda hľadáme najdlhšiu opakovaciu choreografiu pre 10 krúžkov, musíme tieto krúžky rozdeliť na niekoľko cyklov, pričom súčet ich dĺžok bude 10. Pritom chceme maximalizovať najmenší spoločný násobok týchto čísel. Nebude trvať dlho a zistíme, že najlepšie riešenie je spraviť choreografiu skladajúcu sa z troch cyklov dĺžok 2, 3 a 5 a táto choreografia sa prvýkrát zopakuje po \(30\)-tich krokoch.
V ďalších podúlohách budeme využívať algoritmus hľadania najmenšieho spoločného násobku čísel pomocou ich prvočíselných rozkladov. Ak ste sa s týmto algoritmom (prípadne ani s rozkladmi na prvočísla) ešte nestretli, odporúčame vám najprv si o tom niečo naštudovať z iných zdrojov.
Podúloha d)
V tejto podúlohe bolo treba nájsť čo najmenšiu opakovaciu choreografiu, ktorá sa zopakuje po \(3\,960\) skokoch. Z predchádzajúcej podúlohy vieme, že opakovacia choreografia sa musí skaldať z niekoľkých cyklov. A tiež vieme, že najmenší spoločný násobok dĺžok týchto cyklov musí byť nami požadované číslo \(3\,960\).
Samozrejme, môžeme spraviť jeden cyklus dĺžky \(3\,960\). Použiť ale takmer štyritisíc krúžkov asi nebude najlepšie.
Prvočíselný rozklad čísla \(3\,960\) je \(3\,960 = 2^3 \cdot 3^2 \cdot 5 \cdot 11\). Keďže \(3\,960\) má byť najmenší spoločný násobok dĺžok cyklov, všetky tieto prvočísla musia byť niekde v prvočíselných rozkladoch týchto dĺžok. Niektorá z dĺžok teda musí byť deliteľná jedenástimi, niektorá (možno tá istá a možno iná) musí byť deliteľná piatimi. Ďalej musí byť niektorá z dĺžok cyklov deliteľná \(3^2\) – nestačí, aby sme mali dve dĺžky deliteľné \(3\), lebo jedna z týchto troják by sa pri hľadaní najmenšieho spoločného násobku škrtla. Podobne musí byť niektorá z dĺžok deliteľná \(2^3\).
Najmenší súčet dĺžok cyklov (a teda aj najmenší počet krúžkov v našej choreografii) za splnenia týchto podmienok dostaneme, keď zvolíme štyri cykly s dĺžkami 5, 8, 9 a 11 krúžkov. Ľahko overíme, že najmenší spoločný násobok týchto štyroch čísel je naozaj \(3\,960\), teda choreografia sa naozaj prvýkrát začne opakovať po \(3\,960\) zapískaniach. Spolu sme pri tom použili iba 33 krúžkov.
Podúloha e)
Výsledok v podúlohe d) je pomerne malý. Je však najmenší možný? Ako vieme robiť niečo takéto pre všeobecné \(n\)? Budeme postupovať podobne, ale všeobecne. Nech prvočíselný rozklad čísla \(n\) je
\[n = p_1^{\alpha_1} \cdot p_2^{\alpha_2} \cdot \ldots \cdot p_k^{\alpha_k} \text{,}\]
kde \(p_1, p_2, \dots, p_k\) sú navzájom rôzne prvočísla, \(\alpha_1, \alpha_2, \dots, \alpha_k\) sú prirodzené čísla a \(k\) je počet rôznych prvočísel v rozklade. Nenechajte sa zmiasť tým, ako zápis s troma bodkami vyzerá a nemyslite si, že \(k\) musí byť najmenej \(4\). Pokojne to môže byť aj menej, napríklad \(1\) (vtedy by rozklad mal tvar \(n = p_1^{\alpha_1}\)). Dôležité je, že každé prirodzené číslo \(n\) väčšie ako \(1\) sa dá zapísať takýmto spôsobom. Napríklad pre číslo \(3\,960\) by sme mali \(k = 4\), \(p_1 = 2\), \(p_2 = 3\), \(p_3 = 5\), \(p_4 = 11\), \(\alpha_1 = 3\), \(\alpha_2 = 2\), \(\alpha_3 = 1\) a \(\alpha_4 = 1\).
Predstavme si, že za nami prišla víla Amálka a dala nám hotové najlepšie riešenie našej úlohy, teda opakovaciu choreografiu, ktorá sa prvý krát zopakuje po \(n\) zapískaniach a má najmenší možný počet krúžkov. Aké vlastnosti musí táto choreografia mať?
Keďže ide o opakovaciu choreografiu, určite bude pozostávať z niekoľkých cyklov. Navyše vieme, že najmenší spoločný násobok ich dĺžok musí byť \(n\).
Pozrime sa teraz na prvočíselný rozklad dĺžky \(d\) jedného cyklu. Mohlo by v ňom byť viac ako jedno prvočíslo? Povedzme, že áno. Potom by sme túto dĺžku vedeli zapísať ako \(d = q_1^{\beta_1} \cdot q_2^{\beta_2} \cdot \ldots \cdot q_x^{\beta_x}\), kde \(q_1, q_2, \dots, q_x\) sú navzájom rôzne prvočísla, ich počet \(x\) je aspoň 2 a \(\beta_1, \beta_2, \dots, \beta_x\) sú prirodzené čísla. Ak by sme náš cyklus nahradili dvoma cyklami s dĺžkami \(a = q_1^{\beta_1}\) a \(b = q_2^{\beta_2} \cdot \dots \cdot q_x^{\beta_x}\), najmenší spoločný násobok dĺžok všetkých cyklov by sa nezmenil – v rozkladoch dĺžok by boli stále tie isté prvočísla v tých istých mocninách a škrtli by sa nám tie isté prvočísla, čo predtým. Zároveň by sme však takouto výmenou znížili počet krúžkov v choreografii, keďže platí \(a + b < a \cdot b = d\)1. Keďže ale vieme, že Amálka nám už dala najmenšiu možnú choreografiu, tento prípad nemohol nastať. To znamená, že dĺžka nášho cyklu musí mať v rozklade iba jedno prvočíslo (ktoré ale môže byť v ľubovoľne vysokej mocnine). Toto musí platiť pre každý cyklus.
Keďže \(n\) musí byť najmenším spoločným násobkom dĺžok našich cyklov, dĺžka niektorého z cyklov musí mať vo svojom prvočíselnom rozklade \(p_1^{\alpha_1}\). Podobne musí existovať cyklus, ktorý má v rozklade \(p_2^{\alpha_2}\), atď. až po \(p_k^{\alpha_k}\). Všetky tieto cykly musia byť rôzne, nakoľko dĺžka žiadneho cyklu v Amálkinej choreografii nemôže mať v prvočíselnom rozklade dve rôzne prvočísla. V Amálkinom riešení teda určite bude aspoň \(k\) cyklov, ktorých dĺžky budú najmenej \(p_1^{\alpha_1}, p_2^{\alpha_2}, \dots, p_k^{\alpha_k}\). Zároveň platí, že v riešení už nič ďalšie netreba (lebo najmenší spoločný násobok týchto čísel je \(n\)), teda optimálne riešenie bude pozostávať s \(k\) cyklov s dĺžkami \(p_1^{\alpha_1}, p_2^{\alpha_2}, \dots, p_k^{\alpha_k}\).
Podúloha f)
Tu existuje viacero ľahkých postupov, ako vytvoriť takúto neurčitú choreografiu. Napríklad si môžeme zobrať ľubovoľnú opakovaciu a ľubovoľnú stretávaciu choreografiu s aspoň dvoma krúžkami, nakresliť ich do jedného obrázka a krúžky očíslovať tak, aby žiadne dva nemali rovnaké číslo.
Alebo môžeme zobrať ľubovoľne dlhý cyklus, napríklad cyklus dĺžky tri a pridať ešte jeden krúžok, do ktorého nevedie žiadna šípka a vychádza z neho šípka do nejakého krúžku na cykle. Blška začínajúca v krúžku mimo cyklu sa nebude vedieť vrátiť späť (takže choreografia nie je opakovacia) a blšky na cykle sa nikdy nestretnú (takže nie je ani stretávacia).
Podúloha g)
Veľmi ľahko nájdeme choreografiu, v ktorej bude trvať 46 krokov, kým sa všetky blšky stretnú na jednom mieste. Nakreslíme cyklus dĺžky 47, vyberieme si jeden krúžok a zmažeme šípku, ktorá z neho vedie. Následne mu dokreslíme slučku, teda šípku, ktorá pôjde z neho späť doňho. V podstate takto vytvoríme dlhú cestu, kde sa blšky budú stretať práve v tomto pozmenenom krúžku. A blška začínajúca na krúžku, do ktorého nevedie žiadna šípka, bude musieť skočiť 46 krát, aby sa stretla s ostatnými.
Týmto však náš dôkaz nekončí. Zatiaľ sme ukázali len to, že Marienka musí povedať aspoň číslo 46. Ešte musíme ukázať, že neexistuje stretávacia choreografia so 47 krúžkami, v ktorej sa blšky prvýkrát stretnú po viac ako 46 skokoch.
Uvedomme si nasledovnú vlastnosť. Ak sa blška počas vystúpenia druhýkrát ocitne v krúžku, v ktorom už niekedy bola, určite je na cykle, po ktorom bude skákať do nekonečna. Keď totiž bola v tomto krúžku prvýkrát, pokračovala po šípkach ďalej a zaviedli ju naspäť na tento krúžok. Tieto šípky sú jednoznačné, blška sa nemôže rozhodovať o tom, kam chce skočiť. Preto ju zavedú naspäť na tento krúžok aj tretí, štvrtý, … krát.
Po 47 skokoch už každá blška bola v 48 krúžkoch (pretože v jednom krúžku začínala). Keďže krúžkov je iba 47, určite už musela v nejakom krúžku byť aspoň dvakrát. To znamená, že po 47 skokoch bude už každá blška v nejakom cykle. Ba čo viac, každá blška už tento svoj cyklus stihla aj celý prejsť (keďže v niektorom z krúžkov už bola dvakrát). To znamená, že každá blška musela byť v nejakom cykle už skôr – teda už aj po 46 skokoch.
Ak sú dve blšky v nejakom momente v rôznych krúžkoch jedného cyklu, budú po tomto cykle krúžiť dookola s nemeniacim sa odstupom a nikdy sa nestretnú. Tiež sa určite nikdy nestretnú, ak budú v rôznych cykloch. Keďže po 46 skokoch je každá blška v nejakom cykle a navyše vieme, že niekedy sa určite stretnú, jediná možnosť je, že sú všetky v tom istom krúžku, teda už sa stretli. To znamená, že v ľubovoľnej stretávacej 47-krúžkovej choreografii sa všetky blšky stretnú prvýkrát najneskôr po 46 skokoch.
Podúloha h)
Predstavme si stretávacie miesto choreografie, ktorá neobsahuje slučku. Pre každú blšku si vieme zrátať, po koľkých krokoch sa prvýkrat dostane na toto miesto. Musí existovať blška, ktorá sa na stretávacie miesto dostane po \(1\) kroku, nazvime si ju Zuzka. Zároveň musí byť nejaká blška, ktorá začína v stretávacom mieste, nazvime si ju Lucka. Kedže neexistujú žiadne slučky, v každom kroku sa Lucka musí posunúť na iné miesto. A kedže Zuzka sa po prvom kroku ocitne na Luckinom mieste, v druhom kroku sa Zuzka pohne tam, kam sa pohla Lucka v prvom kroku atď. Zuzka sa vždy posunie na to miesto, z ktorého Lucka práve odišla. Zuzka a Lucka sa teda nikdy neocitnú spolu v jendom bode, ale budú sa donekonečne naháňať. To znamená, že choreografia bez slučky nemôže byť stretávacia.
Nerovnosť \(a + b \leq a \cdot b\) platí pre ľubovoľné \(a, b \geq 2\). V našom prípade vieme, že \(a\) aj \(b\) sú aspoň 2, pretože \(a\) je aspoň \(q_1\) (a \(q_1\) je prvočíslo) a \(b\) je aspoň \(q_2\). Navyše, keďže \(q_1\) a \(q_2\) sú navzájom rôzne prvočísla, aspoň jedno z čísel \(a, b\) musí byť väčšie ako \(2\) a preto platí aj nerovnosť \(a + b < a \cdot b\)↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.