Zadanie
Ak máte akékoľvek otázky ohľadom tejto úlohy napíšte Máriovi Lipovskému na
Dvaja vedúci Prasku nedávno cestovali po svete a rozhodli sa, že navštívia väznicu Guantanámo. Šikovní väzni si ich hneď všimli, zobrali im oblečenie a vymenili sa s nimi. Pre stráže všetci vyzerajú rovnako a nikto našim vedúcim neuverí, že tam nepatria. To by predsa mohol povedať každý.
Vedúci si teda musia začať zvykať na väzenský život. Na dennom programe majú skoré budíčky, malé porcie jedla, studené sprchy, žiadny internet a guantanámske šarády. Veľmi sa im to tam nepáči, a tak sa rozhodli utiecť. Nebude to však také ľahké. Skúšali kopať tunel, preliezť plot aj podplatiť stráže, ale nič z toho sa im nepodarilo. Teraz majú nový nápad – utiecť počas obeda. Chcú pri tom využiť fakt, že na obed ich volajú v poradí, v akom sú napísaní vo veľkom zozname väzňov.
Každý väzeň dostal nové meno. Toto meno je zložené z prvých štyroch písmen abecedy a každé písmeno je použité práve raz. Všetky mená sú tiež rovnako dlhé. Takže mená, aké mohli dostať sú napríklad “ABCD” alebo “DCAB”, ale nemohli dostať mená “DAAB”, ani “FGAB”, ani “ABC”. Tieto mená sú zapísané v zozname väzňov v abecednom poradí (presne tak, ako by boli napísané v slovníku). Vedúci potrebujú zistiť viacero vecí pred tým, ako môžu utiecť. Po tom, čo kopali tunel sú ale dosť unavení. Pomôžete im?
Úloha
Okrem samotných odpovedí k úlohám popíšte aj postup, ako ste sa k výsledkom dopracovali.
(2 body) Vedúcich by zaujímalo, koľké v poradí je v zozname väzňov napísané meno “DBAC”.
(3 body) Vedúci sa boja, že ich presunú do najväčšej väznice na svete, kde používajú rovnaký systém mien, akurát každé meno má 15 písmen. Takže prvé v zozname je teraz meno “ABCDEFGHIJKLMNO”. Zistite, koľkým väzňom môže dať takáto väznica meno.
(1 bod) V Guantanáme nedávno prešli na 5-písmenové mená, lebo mali príliš veľa väzňov. Vedúci si všimli, že ich mená začínajú na písmeno D. ,,To je ale náhoda,’’ povedali si. Aby vedeli, aká veľká náhoda to naozaj je, máte im povedať, koľko väzňov dokopy môže mať meno začínajúce na D.
(1 bod) Pri úteku im bude pomáhať väzeň DABCE. Chcú vedieť, koľký v poradí je napísaný v zozname on.
(2 body) Počas obeda budú mať veľmi málo času na útek. DABCE bude utekať prvý a DEABC posledný. Spočítajte, koľko väzňov je medzi nimi v zozname.
(6 bodov) Útek sa nepodaril a Guantanámo sa rozhodlo zvýšiť bezpečnosť. Ako jedno z opatrení prešli na dlhšie mená a vedúcim by sa zišlo nájsť algoritmus, ktorý by im vedel povedať koľké v poradí je hocijaké meno zapísané v slovníku. Vymyslite a popíšte, ako funguje takýto algoritmus. Skúste aj dokázať, že správne určí poradie každého mena. Ukážte, ako by fungoval na konkrétnych menách “FACDEB”, “AEGFDBCH”, “DIECAHFGB” a “BHACDEFGJI”.
Algoritmus je postup jednoduchých krokov, pomocou ktorých vyriešime problém – zistíme poradie mena v zozname. Algoritmus musí tiež zistiť správne poradie pre ľubovoľné meno, ktoré spĺňa všetky podmienky zadania – každé písmeno len raz a meno obsahuje prvé písmena abecedy.
Dajte si pozor na to, že v zozname sú vždy napísané len rovnako dlhé mená – teda ak rátame poradie slova “ABCDEF”, tak bude prvé, lebo nie je žiadne slovo dĺžky 6, ktoré spĺňa podmienky a ktoré by v abecede ležalo pred “ABCDEF”.
Táto úloha bola zameraná na to, aby ste sa naučili lepšie pracovať s permutáciami, ktoré určite využijete ako v programovaní, tak aj v matematike. Permutácia \(n\) prvkov je nejaké poradie \(n\) prvkov, také, že každý prvok využijeme práve raz. Dve permutácie sú rozdielne práve vtedy, keď majú aspoň na jednej pozícii rozdielne prvky. Napríklad \((1, 5, 2, 4, 3)\) je jednou z permutácií čísel \((1, 2, 3, 4, 5)\). V úlohe sme pracovali s permutáciami prvých písmen abecedy.
Podúloha a.
V prvej podúlohe ste mali zistiť, koľké v poradí je konkrétne meno v zozname – koľká v poradí je permutácia písmen “DBAC” v abecedne usporiadanom zozname všetkých permutácií. Keďže meno nie je až tak dlhé, všetkých možných permutácií tiež nebude až tak veľa a môžeme ich skúsiť všetky vypísať. Ako to však urobiť jednoducho?
Začneme permutáciami začínajúcimi na A a budeme pokračovať v abecednom poradí. Tak si budeme istí, že sa nám žiadna permutácia nezopakuje a že ich vypíšeme všetky.
Najprv si vypíšeme všetky permutácie začínajúce písmenom A. Pozrime sa na to, čo môže byť druhé písmeno. B, C alebo D (A to byť nemôže, lebo je už použité). Z nich je prvé v abecede B, takže vypíšeme všetky permutácie začínajúce dvojicou písmen AB. Existujú dve – “ABCD” a “ABDC”. Ďalšie permutácie získame, až keď zmeníme druhé písmeno permutácie, čím dostaneme prvé dve písmená AC. Týmito písmenami začínajú permutácie “ACBD” a “ACDB”. Dvojicou “AD” začínajú permutácie “ADBC” a “ADCB”. Keď sa nám minú permutácie začínajúce na A, zmeníme prvé písmeno na B.
Možno ste si všimli, že v našom postupe si vyberieme prvé písmeno, a potom k nemu pripíšeme všetky permutácie zostávajúcich troch písmen. Keď sme si určili A ako prvé písmeno, zostali nám tri písmená – B, C, D. “BCD”, “BDC”, “CBD”, “CDB”, “DBC” aj “DCB” sú permutácie týchto troch písmen. Ak určíme ako prvé písmeno B, za neho napíšeme všetky permutácie trojice “ACD”, atď.
Takýmto postupom vypíšeme všetky permutácie, a teda:
ABCD ABDC ACBD ACDB ADBC ADCB
BACD BADC BCAD BCDA BDAC BDCA
CABD CADB CBAD CBDA CDAB CDBA
DABC DACB DBAC DBCA DCAB DCBATu si ľahko spočítame, že hľadaná permutácia (DBAC) je na 21. pozícii. Na túto podúlohu bola rozpisovacia metóda postačujúca, lebo nemáme veľa mien, iba 24.
Rýchlejší postup by bol všimnúť si, že máme 6 permutácií začínajúcich písmenom A. Vieme, že permutácií začínajúcich na B aj na C je tiež 6 (rozmyslite si, prečo ich je rovnako veľa). Pred prvou permutáciou začínajúcou na D máme teda 18 permutácií začínajúcich A, B alebo C. Zostali nám už len permutácie začínajúce D-čkom a stačí nám teda už len zistiť poradie “DBAC” medzi nimi.
Podúloha b.
Pokračujeme druhou podúlohou. Chceme zistiť počet permutácií, ak máme 15 písmen. 15 je ale dosť veľké čislo, a tak to najprv skúsime s menším počtom – 4, rovnako ako v prvej podúlohe.
Skúsme si vyrobiť permutáciu. Na prvé miesto si môžeme zvoliť jedno zo 4 písmen – A, B, C, D. Na druhé miesto zostávajú 3 možnosti. Na tretie už len 2 a na posledné miesto dáme to jediné písmeno, ktoré nám zostalo. Situáciu pekne vidíme v strome permutácií.
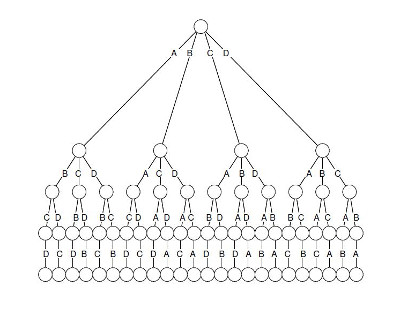
Strom permutácií
V tomto strome máme úplne hore prvé miesto permutácie. Podľa toho, aké písmenko si vyberieme ako prvé, sa rozhodneme pre jeden zo štyroch menších stromov. Podľa toho, ktoré písmenko si vyberieme ako druhé, pokračujeme danou vetvou smerom dole. Na úplne spodnom poschodí stromu je 24 krúžkov – každý z nich predstavuje jednu permutáciu, ktorú zistíme podľa šípok, ktoré ku krúžku vedú. Takže napr. krúžok úplne napravo predstavuje permutáciu “DCBA”, ten naľavo od neho zasa “DCAB”. Krúžkov je dokopy 24 a teda máme 24 možných permutácií.
Tu si môžeme začať všímať, ako sa dá všeobecne počítať počet permutácií. Na prvé miesto vieme vybrať jeden zo štyroch prvkov, na druhé jeden z 3, na tretie už len z jeden dvoch a na posledné miesto nám zostal jediný prvok.
Na hornom poschodí stromu tak vychádzajú z krúžku 4 vetvy, na druhom poschodí vychádzajú z krúžkov 3 vetvy smerom dole, na ďalšom poschodí 2 vetvy z každého krúžku a na predposledom poschodí z krúžkov vychádza len 1 vetva.
Ak je počet krúžkov na spodnom poschodí rovnaký ako počet permutácií, stačí nám spočítať počet krúžkov. Tých je \(4 \cdot 3 \cdot 2 \cdot 1 = 24\) a tak aj celkový počet permutácií je 24.
Keď chceme zistiť počet permutácií pre 15 písmen, môžeme si opäť skúsiť nakresliť takýto strom, lenže veľmi rýchlo narastie do enormných rozmerov. Je ale zrejmé, že na prvé miesto môžeme vybrať jedno z pätnástich písmen, na druhé už len jedno zo štrnástich, na tretie jedno z trinástich a tak ďalej. Takže to bude \(15 \cdot 14 \cdot 13 \cdot 12 \cdot \dots \cdot 3 \cdot 2 \cdot 1\).
Keďže sa táto operácia (vynásobebie všetkých čísel od 1 po \(n\)) využíva často, matematici jej dali názov – faktoriál – a označujú ju výkričníkom za číslom. Môžme povedať, že počet permutácií pätnástich písmen je faktoriál 15 alebo matematicky zapísané ako \(15!\). Všeobecne, počet permutácií \(n\) písmen je \(n!\).
Na zisťovanie počtu permutácií sa dá pozrieť aj inak. Takýto pohľad sa obzvlášť zíde v ďalších podúlohách. Permutácie vytvárame tak, že si vyberieme jedno z písmen (napr. B) a dáme ho na prvé miesto. Potom za toto písmeno napíšeme všetky permutácie zvyšných písmen (A, C, D, E, …). Takto dostaneme všetky permutácie začínajúce na toto písmeno (na písmeno B).
Označme si \(p(15)\) počet permutácií 15 prvkov a predošlú úvahu vieme zapísať ako \(p(15)=15 \cdot p(14)\). Všeobecne, ak by sme si povedali že \(p(n)\) bude počet permutácií \(n\) prvkov tak \(p(n)=n \cdot p(n-1)\). Ak by sme chceli počítať počet permutácií 15 prvkov, môžeme podľa vzorca postupovať takto: \[p(15) = 15 \cdot p(15-1) = 15 \cdot 14 \cdot p(14-1) = 15 \cdot 14 \cdot 13 \cdot p(13-1) = \dots = 15 \cdot 14 \cdot 13 \cdot 12 \cdot \dots \cdot 3 \cdot 2 \cdot p(2-1)\] Keďže vieme, že permutácia jedného prvku je len jedna, tak \(p(1) = 1\) a skutočne \(p(15) = 15! = 1307674368000\).
Podúloha c.
Prejdime k tretej podúlohe, kde bolo treba zistiť koľko 5-prvkových permutácií začína písmenom D. Všimnime si, že akonáhle si určíme prvé písmeno, zostanú nám 4 voľné písmená (A, B, C a E) a 4 voľné pozície. Chceme teda zistiť, koľko rôznych permutácií vieme vytvoriť z týchto 4 písmen. Použijeme znalosti z predchádzajúcej podúlohy a vieme, že to je práve \(4! =4 \cdot 3 \cdot 2 \cdot 1 = 24\).
Úvahu si môžeme aj zovšeobecniť. Ak máme permutáciu \(n\) písmen a nejakému z písmen určíme miesto, zostane nám \(n-1\) písmen a \(n-1\) miest. Potrebujeme teda vedieť počet permutácií \(n-1\) prvkov, čo bude \((n-1)!\). Rozmyslite si, že rovnaký princíp by platil, ak by sme si stanovili nie prvé písmeno ale napr. tretie písmeno – teda že počet permutácií, kde je tretie písmeno B je rovnaký, ako počet permutácií, kde je prvé písmeno D.
Podúloha d.
V štvrtej úlohe ste mali zistiť poradie konkrétneho mena “DABCE” v zozname všetkých 5-písmenových permutácií. Vieme, že D je štvrté v abecede, takže pred “DABCE” musia byť v zozname permutácie začínajúce na A,B a C. V predošlej úlohe sme zistili, že \(n\)-písmenových permutácií začínajúcich na nejaké konkrétne písmeno je práve \((n-1)!\). Tu je \(n=5\), lebo máme dokopy 5 písmen. Takže počet permutácií začínajúcich na jedno z troch písmen A, B alebo C je \(3 \cdot (5 - 1)! = 3 \cdot 4! = 3 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 72\). Pretože po prvom písmene nasledujú písmená “ABCE” a tieto písmena sú v abecednom poradí, “DABCE” je prvá permutácia začínajúca na D. Odpoveďou je teda 73.
Podúloha e.
Poznáme miesto permutácie “DABCE”, potrebujeme ešte zistiť miesto permutácie “DEABC”. Potom už bude ľahké spočítať, koľko premutácií je medzi nimi v zozname.
Môžeme použiť podobný postup, ako v minulej podúlohe. Opäť je prvé písmeno D, takže pred “DEABC” muselo byť aspoň 72 permutácií, ktoré nezačínali na D. Ďalej chceme zistiť pozíciu “DEABC” medzi permutáciami začínajúcimi na D. Zoberme si všetky písmená, ktoré môžu byť na druhej pozícii – A, B, C a E. Naša permutácia má na druhom mieste E, a teda pred ňou museli byť všetky permutácie začínajúce na DA, DB alebo DC.
A koľko pemutácií začína na dvoijice DA, DB alebo DC? Uvedomme si, že akonáhle už máme napísané písmená DA, zostávajú nám tri písmená, ktorými môžeme túto permutáciu dokončiť. Takže hľadáme permutácie troch písmen, ktorých je \(3!\). Na dvojice DA, DB alebo DC začína teda \(3 \cdot 3!=18\) permutácií.
Po E už nasledujú písmená v abecednom poradí, takže “DEABC” je prvá permutácia začínajúca písmenami DE. Celkovo je v zozname 72 permutácií začínajúcich na A, B, C a 18 permutácií začínajúcich na dvojice DA, DB, DC. Pred “DEABC” je teda \(72+18=90\) permutácií, a preto je “DEABC” 91. permutácia.
Úloha znela: Koľko permutácií sa nachádza medzi “DABCE” a “DEABC”. Teraz už vieme, že “DABCE” je v zozname 73. a “DEABC” je 91., takže medzi nimi sú permutácie s číslami \(74, 75, 76 ... 90\). To je dokopy \(90 - 73 = 17\) permutácií.
Ak teda budeme vedieť rýchlo zistiť, koľká je daná permutácia, budeme vedieť aj rýchlo spočítať, koľko permutácií je medzi nejakými dvoma permutáciami \(P1, P2\). Stačí spočítať poradie \(P1\) a \(P2\) a tieto poradia odčítať. Musíme si ale dať pozor, či chceme alebo nechceme započítať aj \(P1, P2\).
Podúloha f.
V poslednej úlohe ste mali vymyslieť algoritmus, ktorý by vedel určiť poradie ľubovoľného mena v zozname. Ako sme už videli v predošlých úlohách, poradie permutácie zistíme tak, že spočítame počet permutácií pred ňou. Najprv si zoberieme dostatočne dlhý príklad na to, aby sa na ňom dal popísať postup algoritmu, napr. “FACDEB”.
Vidíme, že prvé písmeno je F, a teda najprv zistíme, koľko permutácií je v zozname pred ľubovoľnou permutáciou začínajúcou na F. Sú to všetky, ktoré začínajú na A, B, C, D alebo E. Vieme, že takýchto permutácií je pre každé písmeno \(5!\), lebo permutujeme zvyšných 5 písmen. Dokopy muselo byť \(5 \cdot 5! = 600\) permutácií, ktoré sú v zozname skôr ako tie, ktoré začínajú na F.
Ďalej chceme zistiť, koľká je permutácia “FACDEB” uprostred tých, čo začínajú na F. F-ko si teda môžeme pomyseľne vyškrtnúť, pretože všetky permutácie, s ktorými budeme ďalej pracovať, ho už majú na začiatku. Chceme teda zistiť, koľká je “ACDEB” medzi všetkými permutáciami písmen A, B, C, D, E. Opäť sa pýtame, koľko permutácií je v zozname pred ľubovoľnou permutáciou začínajúcou na A. V tomto kroku to máme uľahčené, pretože A je medzi A, B, C, D, E najskôr písmeno v abecede a teda pred “ACDEB” nie sú žiadne iné permutácie.
Vymažeme aj A a zostane nám “CDEB”. C je medzi týmito písmenami druhé v abecede, takže pred “CDEB” museli byť permutácie 4 písmen začínajúce na B, a tých je \(1 \cdot 3! = 6\), keďže permutujeme trojicu písmen B, C, E.
Zostala nám trojica písmen “DEB”. D je medzi nimi druhé v abecede, a teda pred “DEB” sú permutácie 3 písmen začínajúce na B, ktorých je \(1 \cdot 2! = 2\).
Keď vyškrtneme D, zostane nám “EB”, a E je medzi nimi druhé v abecede takže pred “EB” sú permutácie 2 písmen začínajúce na B, a tých je \(1!=1\).
Nakoniec nám zostane len “B” a B je prvé v abecede medzi zostávajúcimi písmenami, a teda pred “B” nie sú žiadne permutácie.
Ako teda zistíme poradie “FACDEB” medzi všetkými permutáciami písmen A, B, C, D, E, F?
- Najprv sme teda mali 600 permutácií, ktoré boli v zozname pred prvou permutáciou začínajúcou na F.
- Potom sme mali 0 permutácií, ktoré sa začínali na F, ale druhé písmeno ešte nebolo A.
- Na “FA” začínalo 6 permutácií predtým, než prišla prvá začínajúca na “FAC”.
- Potom nasledovali 2 permutácie, ktoré začínali “FAC” pred prvou permutáciou začínajucou na “FACD”.
- Ďalej 1 permutácia začínajúce na “FACD” pred “FACDE”.
- Na záver 0 permutácií začínajúcich na “FACDE”, ktoré sú pred “FACDEB”.
Pre určenie poradia “FACDEB” nám stačí spočítať všetky permutácie pred ňou. Stačí tak sčítať čísla, čo sme si doteraz zapísali: \(5 \cdot 5! + 0 \cdot 4! + 1 \cdot 3! + 1 \cdot 2! + 1 \cdot 1! + 0 = 600 + 0 + 6 + 2 + 1 + 0 = 609\). Pred “FACDEB” je 609 permutácií, teda jej poradie je 610.
Teraz bude jednoduché zapísať všeobecný postup. Označíme si \(X\) permutáciu, ktorej poradie hľadáme:
Ako zistiť, koľko permutácií bolo pred permutáciou X:
Výsledok je zatiaľ 0.
Opakuj, kým je v X aspoň 1 písmeno:
Zistíme počet písmen v X, a označíme si ho n
Zistíme počet písmen v X, ktoré sú v abecede pred prvým písmenom X, a označíme si ho p
K výsledku pripočítame p*(n-1)!
Odstránime z X prvé písmenoKeďže permutácia \(X\) bola konečne dlhá a vždy z nej odstraňujeme jedno písmeno, po nejakom čase sa určite dostaneme do momentu, kedy nám nezostane žiadne písmeno. Vieme tak, že algoritmus vždy skončí.
Druhou podmienkou, ktorú požadujeme od algoritmu je, aby vypočítal správne riešenie. V úlohe c. sme si ukázali, že permutácií \(n\) písmen, kde je pevne určené prvé písmeno je \((n-1)!\). Algoritmom sme sčítali všetky permutácie pred danou permutáciou: v prvom opakovaní všetky tie, ktoré sa líšia v prvom písmene, v druhom opakovaní tie ktoré majú rovnaké prvé písmeno ale iné druhé, atď. Započítali sme teda každú permutáciu pred \(X\) práve raz.
Pokiaľ ste prišli na algoritmus, bolo ho ešte potrebné využiť na zistenie poradia niekoľkých permutácií. Toto už bola jednoduchá práca s kalkulačkou, len bolo potrebné niekoľkokrát zopakovať tento postup.
Poradia permutácií sú nasledovné, no za numerické chyby body nestratíte.
FACDEB – 610, AEGFDBCH – 2725, DIECAHFGB – 158662, BHACDEFGJI – 604802
Tí, čo vedia programovať si mohli uľahčiť prácu oproti ručnému vypisovaniu a počítaniu faktoriálov na kalkulačke.
#include <iostream>
#include <string>
using namespace std;
int Faktorial[20];
int main() {
Faktorial[0]=1;
for(int i=1; i<20; i++) Faktorial[i] = i*Faktorial[i-1];
string s;
cin >> s;
int vysledok=0;
int n=s.length();
for(int i=0; i<n; i++) {
int mensie=0;
for(int j=i; j<n; j++)
if(s[j]<s[i]) mensie++;
vysledok += mensie*Faktorial[n-i-1];
}
cout << vysledok << endl;
}from math import factorial
X = input()
vysledok = 0
while len(X) > 0:
n = len(X)
p = 0
for pismeno in X:
if pismeno < X[0]:
p += 1
vysledok += p * factorial(n-1)
X = X[1:]
print(vysledok)Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.