1. Prazvláštne artefakty
Zadanie
Táto úloha je špeciálna. Odovzdávaš aj popis, aj riešiš podúlohy v našom editore, za ktoré dostaneš body automaticky. Ak máš akékoľvek otázky ohľadom tejto úlohy, napíš Andrejovi na [email protected]
Táto úloha je identická s úlohou KSP - Existenčná kríza. KSP je súťaž určená najmä pre stredoškolákov, ale aj ak si mladší, tak sa môžeš kľudne skúsiť zapojiť. V tom prípade ale musíš programy aj popisy odovzdať aj na stránke Prasku, aj na stránke KSP.
MisQo nenosil respirátor a dostal existenčnú krízu. Teraz mu nedajú spať otázky ako napríklad:
- “čo je to TLB a aké má využitie?”,
- “má jazyk generovaný turingovym strojom danú netriviálnu vlasnosť?”,
- “aký bol tvoj názor na voľný program? bolo ho málo alebo veľa?”
- “kedy vyjde nový Taylor Swift album?”
- a, samozrejme, “aká je odpoveď na otázku Života, Vesmíru a Všetkého?”.
Tak sa raz MisQo jedného dňa prechádzal po Ikei, dumajúc nad týmito existenčnými otázkami, keď tu zrazu začul tiché “Pšt!” 1. Obzrel sa, a uvidel záhadnú postavu v kabáte, ktorej nebolo vidno do tváre. Teda možno to bolo tým, že mala len pár centimetrov. Piskľavý hlas oznámil “tento počítač má všetky odpovede, ktoré hľadáš…”. MisQo s nadšením pochybný obchod prijal a domov priniesol masívnu krabicu. Keď ju však doma otvoril, čakalo ho prekvapenie. V krabici bolo iba zrkadlo a kryptický nápis “Kľúčom si ty sám…”. MisQo si to, samozrejme, vyložil tak, že všetky súčiastky budú nechcené veci, ktoré nájde vo svojom byte.
Po prehrabaní zopár kútov našiel nasledovné artefakty, z ktorých každý má nejakú ikonickú funkciu:
- starožitný želé dávkovač ($z$), ktorý už dávno nemá želé. Jeho funkcia je taká, že vždy vracia $0$.
- inhalátor ($i$) plný veľmi priľnavých trblietok, ktoré skrášlia čokoľvek, čoho sa dotknú. Jeho funkcia je taká, že čokoľvek je na vstupe, vráti o $1$ zvýšené.
- nekonečná sada ($s$) zberačov odpadkov všetkých možných dĺžok. Pre každé prirodzené číslo $n$ sa nájde nejaký zberač $s_n$, ktorého funkcia je taká, že vráti $n$-tú hodnotu zo svojho vstupu.
- odniekiaľ zo steny vytiahnutú kovovú trubku ($K$), do ktorej sa dá nasypať niekoľko iných artefaktov. Jej funkcia je taká, že na svojich vstupoch spustí všetky tieto artefakty, až na prvý, ktorý spustí až na konci, na výsledkoch všetkých predošlých.
- prastarý rotor ($R$), na ktorý sa dá pripevniť nejaký iný artefakt, aby svoju funkciu vykonal niekoľkokrát za sebou. Jeho funkcia je taká, že zo vstupu prečíta číslo, a toľkokrát spustí na zvyšku vstupu artefakt, ktorý sa na ňom točí.
Teraz by MisQo rád zostrojil počítače, ktoré mu dajú odpovede na jeho kritické otázky. Samozrejme, s takto skromnými materiálmi to nie je vôbec triviálne. MisQovi sa veľmi nechce, a tak je na vás, aby ste pre neho tieto počítače zostrojili…
Úloha
Táto úloha sa rieši interaktívne a môžete ju riešiť tu. Tam aj nájdete podrobnejšie pokyny k tomu, ako fungujú jednotlivé artefakty a ako sa z nich dajú skladať počítače.
K tejto úlohe píšete aj popis. Pre každú podúlohu by mal popis obsahovať maximálne 5 viet, kde opíšete, čo ste vlastne urobili a prečo to funguje a screenshot programu. Nemusí obsahovať žiadnu analýzu zložitosti ani nič podobné.
Každá podúloha má 5 bodov za program a 5 bodov za popis. Body za program sa ti pripočítajú automaticky, keď odovzdáš správny program, body za popis dostaneš niekedy po konci kola.
Pokiaľ pri podúlohe nie je uvedené inak, tak si vstupy označíme postupne $a$, $b$, $c$, …
a. nula
Na to, aby sme zavolali Zero bez vstupov, využijeme Kompozítor a Repeater.
Kompozítor vyžaduje aspoň dva bloky, z čoho vyplýva, že final blok dostane
vždy aspoň jeden vstup. Kompozítor tak vieme využiť na eliminovanie počtu
vstupov na jeden.
Teraz sa pozrieme na Repeater - ako prvý vstup berie počet opakovaní a ostatné
vstupy sú voliteľné. Keď Repeater zavoláme s jedným vstupom, tak init
nedostane žiadny vstup, čiže ako init vieme dať Zero. Už len si potrebujeme
túto hodnotu udržať, a tak step musí vždy vrátiť priebežnú hodnotu. Na to už
len použijeme Selektor.

b. +3
Použijeme vnorené Kompozítory, aby sme postupne 3× zavolali Increment na vstupe.
Skúste si uvedomiť, že pomocou podúlohy a. takto vieme vyrobiť ľubovoľnú nezápornú konštantu s ľubovoľným počtom vstupov.

c. násobenie
Násobenie spravíme pomocou postupného sčítania (to je vysvetlené v tutoriáli. Pomocou Repeatera budeme volať sčítavanie, ktoré zoberie predchádzajúcu hodnotu a druhý vstup Repeatera.
A čo bude počiatočná hodnota Repeatera? Takýmto spôsobom $a$ krát pripočítame $b$, čiže začiatočná hodnota musí byť $0$. Na to môžeme využiť nulu z podúlohy a.
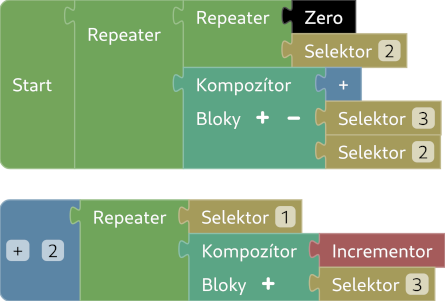
d. decrement
Trik spočíva v tom, že Repeater počíta iterácie od $0$ po $n-1$. Použijeme
Repeater s počiatočnou hodnotou $0$ (špeciálny prípad a step vráti číslo
iterácie.

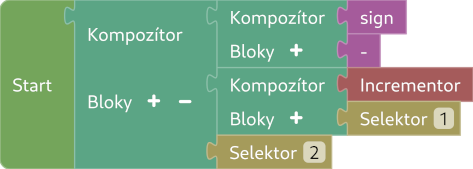
e. odčítanie
Odčítanie spravíme podobne ako sčítanie, ale použijeme decrement namiesto Incrementora a vymeníme poradie vstupov pomocou Kompozítora, aby sme sme odčítali $b$ číslo od $a$.

f. umocňovanie
Obdobne ako sme pri násobení použili sčítanie, teraz použijeme násobenie. Avšak tento krát počiatočná hodnota bude $1$ (keby sme nechali $0$, tak výsledok bude vždy $0$, čiže použijeme pozorovanie z podúlohy b. Nakoniec ešte musíme vymeniť poradie vstupov, aby sme $b$ krát vynásobili $a$ a nie naopak.

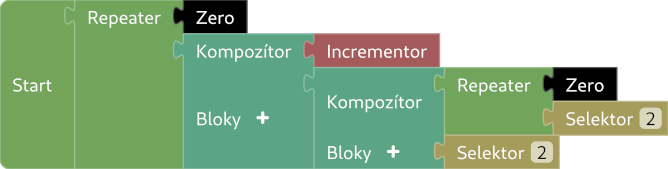
g. sign
Potrebujeme vrátiť $0$, ak je vstup $0$, inak vrátiť $1$. Na to použijeme Repeater - ak $a = 0$, tak Repeater vráti počiatočnú hodnotu cyklu, ktorú nastavíme na $0$. Ak $a > 0$, tak Repeater by mal Repeater vrátiť $1$ - na to vieme opäť použiť pozorovanie z podúlohy b.
h. >=
$a - b$ nám vráti $0$ ak $a \leq b$, v opačnom prípade vráti kladné číslo. My ale
chceme vrátiť iba $0$ alebo $1$ a na to vieme použiť sign z podúlohy g. Takto
dostaneme $0$ ak $a \leq b$ a v opačnom prípade $1$.
Ak chceme dostať $0$ ak $a < b$ a v opačnom prípade $1$, musíme rovnosť posunúť.
Zväčšením $a$ o jedna, dostaneme $a + 1 - b$, ktoré vráti $0$ ak $a < b$ a inak
vráti $1$ (po použití sign.
Skúste si uvedomiť, že podobným spôsobom vieme vytvoriť aj funkcie <, <= a
>.
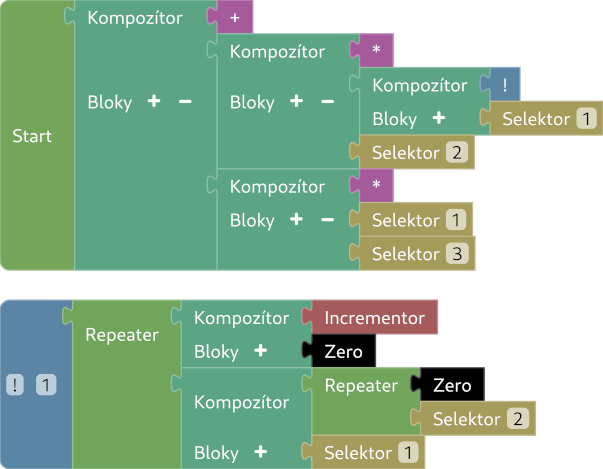
i. if
Označme si vstupy postupne $c$ (condition, $i$ (if a $e$ (else.
Začnime tým, že si definujeme funkciu ! , ktorá zneguje svoj jediný vstup - ak
je $0$, tak vráti $1$, inak vráti $0$. Môžeme si všimnúť, že je to vlastne
sign, len s vymenenými konštantami - init bude $1$ a step bude $0$.
Teraz, keď už vieme znegovať $c$, môžeme si skúsiť úlohu vyjadriť matematicky:
$$ v = !a * c + b * c$$
Ak $c = 0$, tak $v = b$, inak $v = a$, čo je to, čo máme urobiť. A to už vieme urobiť pomocou predchádzajúcich podúloh a vnorených Kompozítorov.
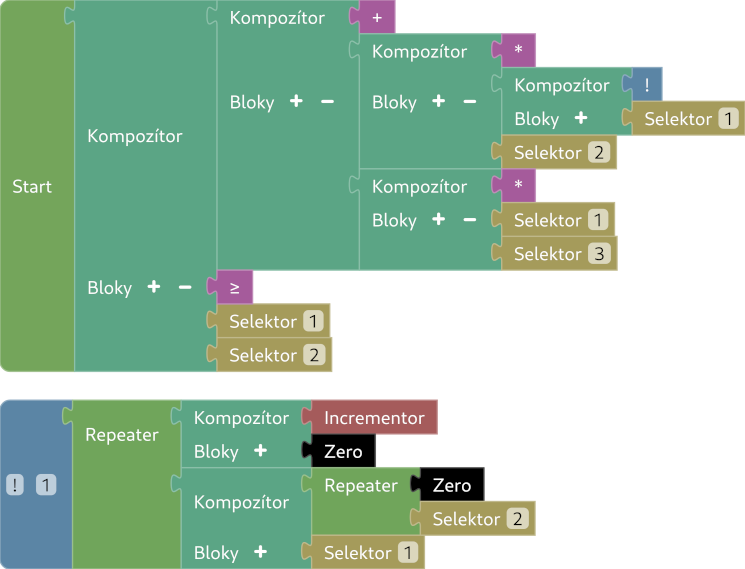
j. min
Táto podúloha sa veľmi podobá na podúlohu i, až na to, že nemáme $c$ na
vstupe. $c$ si vieme získať pomocou podúlohy h. Čiže nám stačí pomocou
Kompozítora a ≥ pretransformovať vstup pre program z podúlohy i.
Skúste si uvedomiť, že max vieme vytvoriť použitím <= z podúlohy h.
k. bonus
Pre detaily ohľadom riešenie pôvodnej úlohy si pozrite vzorák prvej úlohy.
Najskôr si definujme konštanty 10 a 1 s jedným vstupom:

Ďalej si potrebujeme vyrobiť funkciu dist s dvoma vstupmi $a$ a $b$, ktorá
vypočíta vzdialenosť dvoch pozícií (vstupov + 1 (kliknutie.
Vzdialenosť dvoch pozícií je $\text{min}(10 - \text{abs}(a - b, \text{abs}(a - b$
Vieme spraviť všetko, okrem abs. My ale abs nepotrebujeme, stačí nám vždy
odčítavať menšie číslo od väčšieho, čo vieme spraviť ako:
$\text{max}(a, b - \text{min}(a, b$. Túto funkciu si pomenujme dist_help.
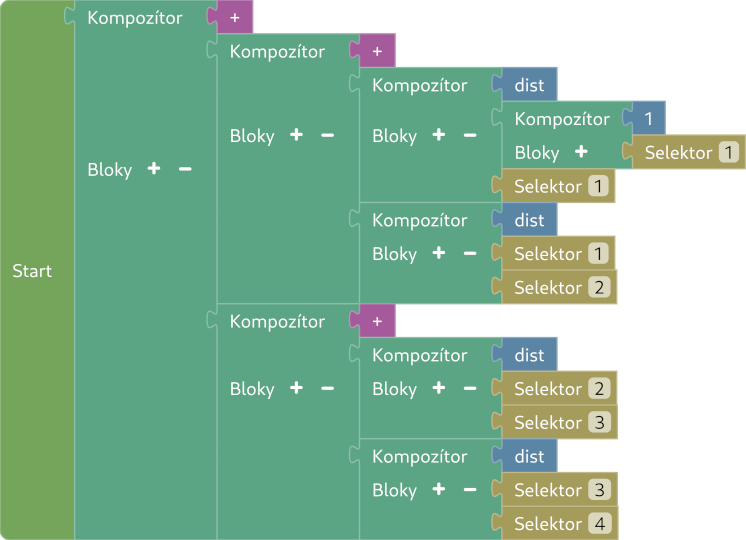
Počítanie vzdialenosti tak vyzerá nasledovne:
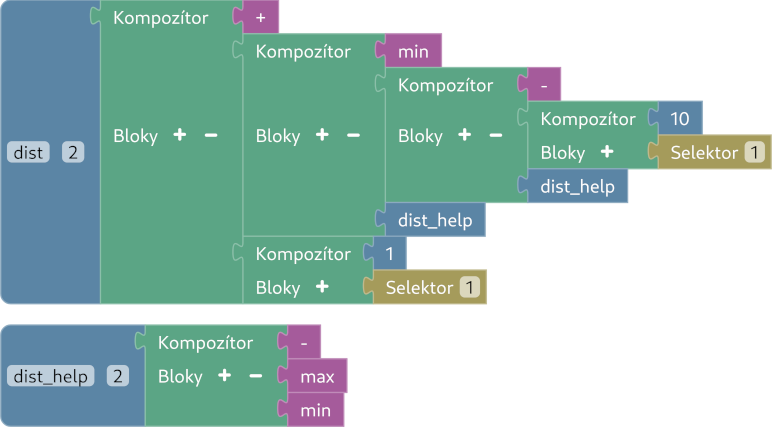
Keď už vieme vypočítať vzdialenosť dvoch pozícií, už len potrebujeme dostať finálny výsledok. To vieme tak, že postupne sčítame medzivýsledky:
$$\text{dist}(1, a + \text{dist}(a, b + \text{dist}(b, c + \text{dist}(c, d$$
Takto dostaneme konečný výsledok ($1$ je počiatočná pozícia, ako je definované v zadaní: