2. Rekreačný cyklista Kubko

Novinka: táto úloha je rozdelená na niekoľko na seba nadväzujúcich sád, za ktoré viete dokopy získať 100 bodov. Zatiaľ máte k dispozícii iba zadania prvej sady. Na získanie zadaní ďalšej sady je potrebné odovzdať riešenia tej predchádzajúcej.

Hocikedy v priebehu kola môžete odovzdať vaše aktuálne riešenie. My vám ho v priebehu pár dní opravíme a pošleme späť aj s komentármi. Ak sa vám podúlohy podarilo vyriešiť správne, dostanete ďalšie zadania. Ak vaše riešenie nebolo správne, nič sa nedeje. V komentári vám skúsime poradiť kde nastala chyba a vy ju môžete opraviť a poslať znova až kým nebudete úspešní.

Veríme, že takto sa vám podarí vyriešiť viac podúloh a teda sa aj viac naučíte. Nabojte sa nám teda poslať aj rozpracované riešenie, alebo také, ktorým si nie ste úplne istí. Nehrozí vám žiadna penalizácia a môžete dostať dobrú radu. Odporúčame však úlohu riešiť priebežne.

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Miškovi na [email protected]

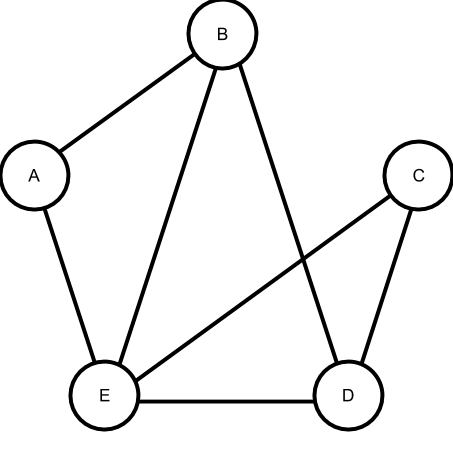
Kubko sa rád bicykluje. V jeho okolí je však len zopár cyklistických chodníkov znázornených na obrázku. Napriek tomu vždy keď má nejaký voľný čas, sadne na bicykel a trénuje. Včera napríklad začal v mieste D, pokračoval cez C do E, potom sa vrátil do D a nakoniec skončil v B. Takúto cestu by sme skrátene zapísali ako D-C-E-D-B a jej dĺžka je 4.

Zajtra by sa chcel ísť znovu bicyklovať, no potrebuje si nájsť novú trasu, lebo ísť dvakrát po tej istej je príliš nudné. Zaujíma ho preto, koľko rôznych ciest určitej dĺžky v okolí existuje.

Sada úloh 1 – Krátke cesty

Kubko je síce zdatný cyklista, no počítanie nie je jeho silnou stránkou. Preto spočítať vhodné cesty pre Kubka ostalo na vás. Ako zvyčajne, budete riešiť niekoľko podúloh zoradených podľa nami odhadovanej zložitosti. Okrem výsledku vždy napíšte, aspoň pár vetami, ako ste sa k danému riešeniu dostali. Odporúčame vám podúlohy riešiť postupne, keďže riešenie jednej môže pomôcť pri riešení ďalšej.

1. (8 bodov) Zistite, koľko je na obrázku rôznych ciest dĺžky \(3\) takých, že začínajú v A a končia v D. Dve cesty sú rôzne ak neprechádzajú tými istými miestami presne v rovnakom poradí. Teda napríklad cesty B-E-D-C a B-D-E-C sú dve rôzne cesty dĺžky \(3\).

2. (10 bodov) Pre každý začiatok a koniec zistite, koľko existuje ciest medzi nimi s dĺžkou práve \(3\). Napríklad počet ciest medzi A a D už poznáte z predošlej podúlohy, ostáva vám to určiť pre zvyšné začiatky a konce. Nezabudnite, že cesty môžu začínať a končiť v tom istom mieste.

3. (8 bodov) Zistite, koľko je takých ciest, ktoré začínajú aj končia v mieste A, majú dĺžku 6 a v strede, teda vo vzdialenosti \(3\), bude Kubko v mieste B. Jedna takáto cesta je napríklad cesta A-E-D-B-A-E-A.

4. (8 bodov) Zistite koľko je takých ciest, ktoré začínajú v A, končia v C a majú dĺžku 6.