1. Prefixová expedícia

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Romanovi na [email protected]

Macín a Ondro sú ostrieľaní lezci a na jar sa rozhodli vyraziť za adrenalínom do Tatier. Pred expedíciou si kúpili turistickú mapu, ktorá vyzerala nasledovne:

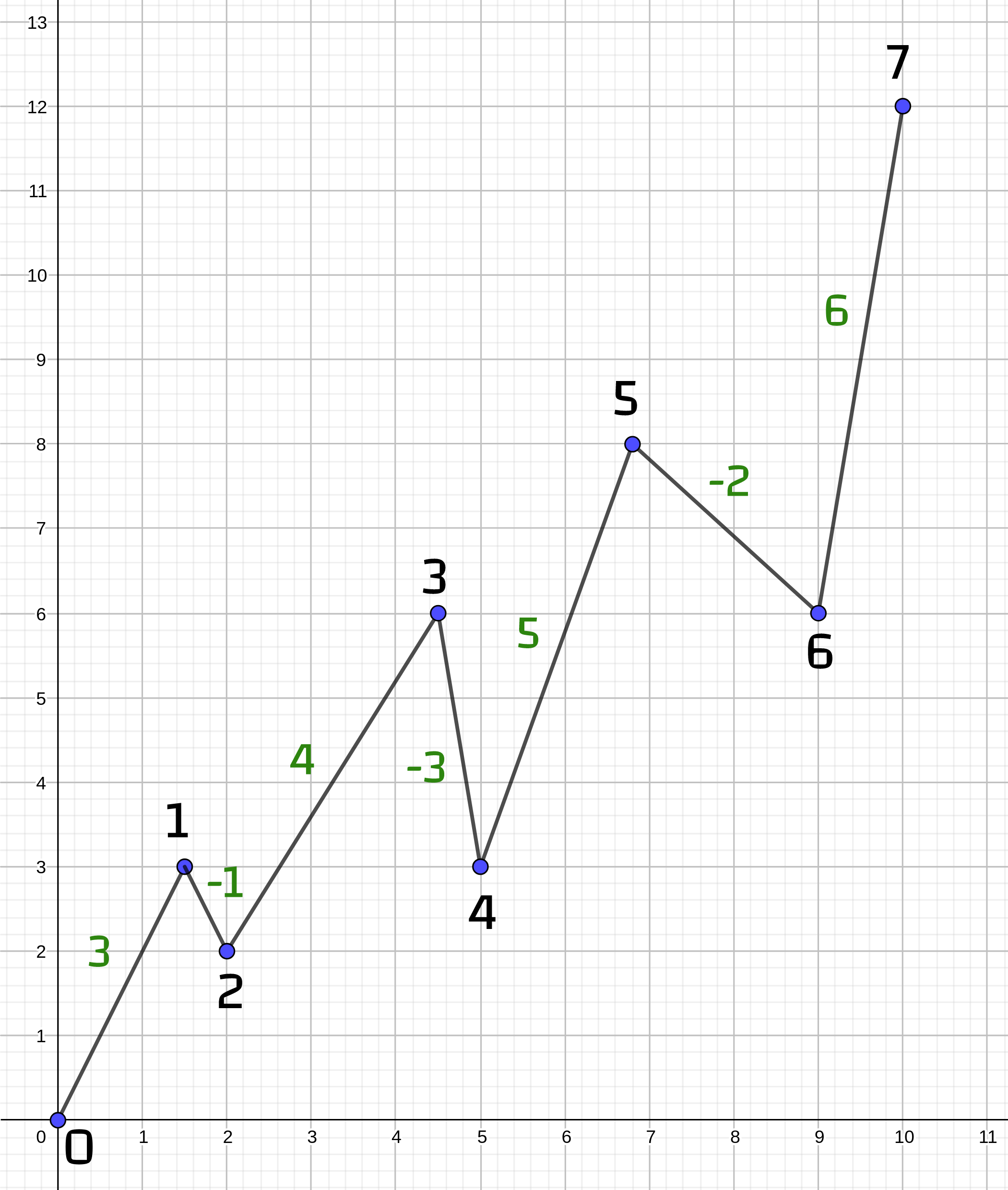
Medzi každými dvoma vrcholmi na mape je jedno číslo, ktoré reprezentuje rozdiel nadmorskej výšky pravého a ľavého vrcholu. Macín s Ondrom sa po mape budú pohybovať zľava doprava. Nevedia však, v ktorom vrchole svoju expedíciu začnú a preto potrebujú pomoc pri výbere trasy.

Úloha

Vrcholy z mapy si očíslujeme zľava doprava \(0\) až \(N\). Údaje o nadmorských výškach budeme reprezentovať pomocou poľa \(A\), ktoré obsahuje jednotlivé rozdiely. Prvok \(A[i]\) obsahuje rozdiel medzi výškou vrchola \(i+1\) a \(i\). Pole \(A\) pre našu mapu vyzerá nasledovne:

Terka chalanom poradila, aby si predpočítali pre pole \(A\) prefixové súčty. Ide o list, na ktorého \(i\)-tej pozícii je súčet všetkých čísel, ktoré sú v pôvodnej postupnosti na pozíciách od \(0\) po \(i - 1\). Pre pole \(A\) bude preto pole \(P\) prefixových súčtov vyzerať nasledovne:

Všimnite si, že tento list je o jedna dlhší ako \(A\) a začína \(0\). Na \(0\)-tej pozícii totiž musí byť súčet čísel od \(0\) po \(−1\), čo je \(0\). Napríklad na \(3\)-tej pozícii je \(6\), pretože súčet prvých \(3\) čísel poľa \(A\) je \(3 - 1 + 4 = 6\).

1. (2 body) Ondru pred cestou zaujíma, kde má mapa svoje stredové vrcholy. Stredový vrchol je taký vrchol, pre ktorý je súčet rozdielov z najľavejšieho vrcholu na mape rovnaký ako súčet rozdielov od najpravejšieho vrcholu na mape. Presnejšie teda hľadáme všetky vrcholy \(k\) také, že \[A[0] + \dots + A[k - 1] = A[k] + \dots + A[N - 1]\] Napríklad na mape zo začiatku zadania sú stredovými vrcholmi vrcholy \(3\) a \(6\). Vymyslite ako efektívne nájsť stredové vrcholy pre pole \(A\). Efektívnym riešením v tomto prípade myslíme také, ktoré pristupuje k jednotlivým prvkov poľa \(A\) a \(P\) čo najmenejkrát. Pošlite nám slovný popis vášho postupu. Váš popis by mal byť zrozumiteľný aj bez znalosti programovania a mal by ho vedieť odsimulovať ktokoľvek s perom a papierom.

2. (2 body) Macín a Ondro plánujú špeciálnu túru, pri ktorej skončia v rovnakej nadmorskej výške, z akej vyrážali. To znamená, že celkový súčet rozdielov nadmorských výšok na trase je rovný \(0\). Viete im poradiť, ako pomocou prefixových súčtov nájsť súvislý úsek v poli \(A\), ktorého súčet je \(0\)? Pri tejto podúlohe neposielajte algoritmus, iba popíšte, ako si v poli prefixových súčtov všimnúť úsek so súčtom \(0\).

3. (3 body) Chalanov pri plánovaní často zaujíma, aký je celkový rozdiel nadmorskej výšky medzi konkrétnymi dvoma vrcholmi. Napríklad pre vrcholy \(2\) a \(5\) je celkový rozdiel \(4 - 3 + 5 = 6\). Všimnite si, že pre vrcholy \(a\) a \(b\) také, že \(a < b\), vieme vypočítať celkový rozdiel ako súčet čiastkových rozdielov, tj. \(A[a] + A[a + 1] + ... + A[b - 1]\). Macín ale stále prichádza s novými nápadmi na trasy a Ondrovi sa už nechce počítať rozdiely prvok po prvku. Musí to ísť predsa lepšie! Vašou úlohou je preto prísť na to, ako šikovne spočítať celkový rozdiel medzi výškami vrcholov \(a\) a \(b\) pomocou poľa prefixových súčtov \(P\).

4. (3 body) Ako pre pole \(A\) vytvoriť pole prefixových súčtov \(P\)? Podobne ako v podúlohe a) vymyslite efektívne riešenie, teda také, ktoré k prvkom poľa \(A\) a \(P\) prístupi čo najmenejkrát, a pošlite nám jeho slovný popis.

5. (5 bodov) Telo sa musí vyššej nadmorskej výške vždy prispôsobiť. Výstupiť preto za jeden deň oveľa vyššie a prenocovať tam by mohlo byť nebezpečné. Chalani si určili výšku \(k\), o ktorú chcú za jeden deň vystúpiť vyššie. Vašou úlohou bude nájsť všetky dvojice vrcholov, medzi ktorými je celkový rozdiel nadmorských výšok práve \(k\). Napríklad na našej mape by pre \(k = 4\) splňovali túto podmienku dvojice vrcholov \((2, 3)\) a \((2, 6)\). Opäť nám pošlite slovný popis čo najefektívnejšieho riešenia.

Ak viete programovať, niektoré z podúloh si môžete vyskúšať naprogramovať a poslať nám vaše kódy. Nedostanete síce body naviac, ale vaše programy okomentujeme a poradíme vám, čo by sa dalo spraviť lepšie alebo krajšie. Pri programátorských úlohách vám nedávame spätnú väzbu k vašim programom, preto máte teraz jedinečnú šancu.

P.S.: Ondro s Macínom a kamarátmi Tatry skutočne navštívili. Ako sa Čechom v Tatrách darilo a či ich zachraňovala horská služba, sa dozviete v článku od Ondru.