Ak nevieš programovať, nezúfaj! Môžeš sa to naučiť a ešte za to získať body, ktoré sa ti budú počítať namiesto tejto úlohy.
Stačí, že pôjdeš na stránku Programátorskej Liahni (liahen.ksp.sk). Keď budeš riešiť sadu conditions_cpp, bodmi, ktoré získaš si môžeš nahradiť riešenie tejto úlohy. Stačí ak na spodku tejto stránky odovzdáš pdf-ko s prezývkou, ktorú používaš na Liahni.
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Romanovi na [email protected]
Jozef sa pri raňajkách zahľadel na chladničku, na ktorej bolo množstvo magnetiek. Sestra Vendula je totiž ich nadšená zberateľka. Svoj prvý kúsok dostala od tety z Gruzínska, ktorá sa vracala z brigády na arašidových plantážach. Vendule sa vtedy magnetka zapáčila natoľko, že od rodiny a kamarátov už nechcela iné darčeky ako magnetky. Tento mesiac nimi konečne zaplnila celú chladničku. Teraz ale nevie, ako magnetky usporiadať.
Jozefa, dojedajúc svoje raňajky, napadlo, že by bolo zaujímavé vytvoriť z magnetiek na chladničke čo najviac rovnakých riadkov. Svoj nápad hneď povedal Vendule a tá bola nadšená. Teraz spolu rozmýšlajú koľko takýchto riadkov vedia vytvoriť. Ponáhľajú sa však do školy, a tak potrebujú pomoc!
Chladničku si pre jednoduchosť predstavme ako mriežku veľkosti \(n \times n\) a magnetky ako znaky +, @, atď. Potom mriežka môže vyzerať napríklad takto:
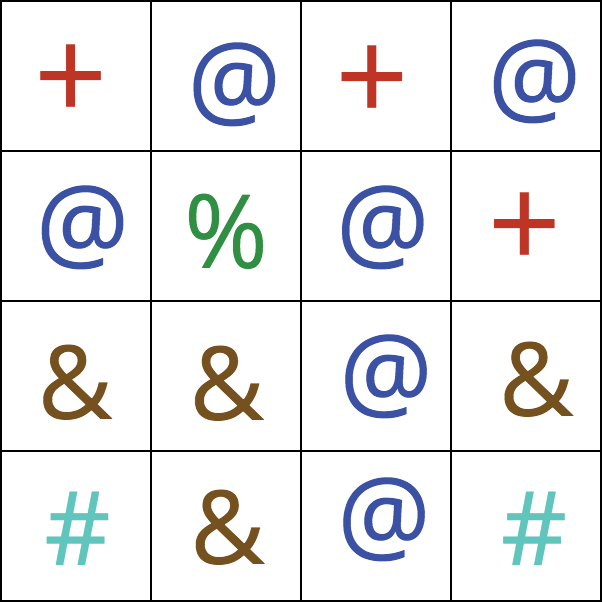
Všimnite si, že znaky v mriežke sa môžu opakovať – inak by sme nemohli vytvoriť rovnaké riadky. Pre mriežku vyššie vieme vytvoriť 3 rovnaké riadky, takže jedno z možných pekných usporiadaní je nasledovné:
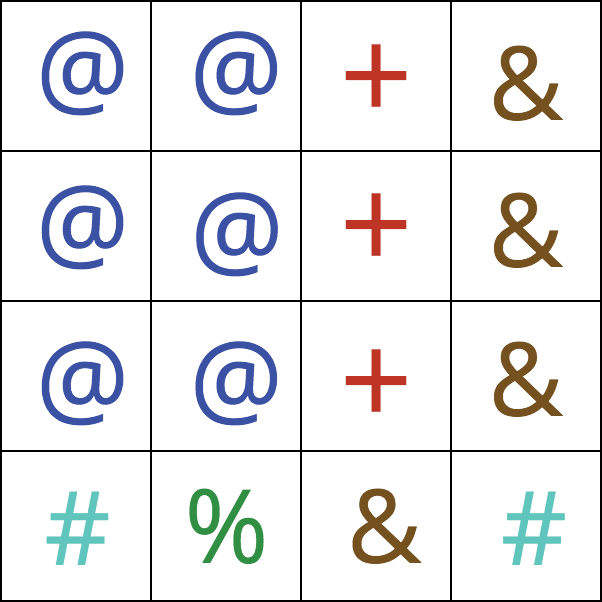
Úloha
Každá mriežka veľkosti \(n \times n\) obsahuje \(n^2\) magnetiek, z ktorých sa ale niektoré môžu opakovať. Počet rôznych magnetiek si označíme \(r\). Na mriežke sa teda vyskytuje \(r\) typov magnetiek: \(t_1, t_2, ..., t_r\). Každý typ \(t_i\) sa môže na mriežke vyskytovať viackrát, takže počet výskytov typu \(t_i\) si označíme \(p_i\). Platí, že: \[p_1 + p_2 + ... + p_r = n^2\]
Napríklad mriežka vyššie obsahuje 5 rôznych symbolov, takže \(r = 5\). Takýto vstup by sa preto dal zapísať pomocou nasledovnej tabuľky:
| \(i\) | \(t_i\) | \(p_i\) |
|---|---|---|
| 1 | + |
3 |
| 2 | @ |
6 |
| 3 | % |
1 |
| 4 | & |
4 |
| 5 | # |
2 |
Variant A
Pre zadanú mriežku a jednotlivé počty magnetiek zistite, či sa dá vytvoriť aspoň \(47\) rovnakých riadkov.
Variant B
Na získanie plného počtu bodov stačí vyriešiť Variant B
Pre zadanú mriežku a jednotlivé počty magnetiek zistite, koľko najviac rovnakých riadkov je možné vytvoriť.
Formát vstupu
Na prvom riadku vstupu dostaneme dve celé čísla \(n\) a \(r\) – veľkosť mriežky \(n \times n\) a počet rôznych magnetiek, ktoré sa na mriežke nachádzajú.
Nasleduje riadok s \(r\) medzerou oddelenými číslami, pričom \(i\)-te číslo reprezentuje počet magnetiek \(p_i\) typu \(t_i\) na mriežke. Samotné typy magnetiek nás nezaujímajú, vieme že všetkých \(r\) je navzájom rôznych.
Pri riešení v jazyku C++, Pascal, Java a podobných, si dávajte pozor na maximálne číslo, ktoré sú schopné celočíselné premenné uložiť. Počet magnetiek jedného typu môže v posledných dvoch sadách tieto limity prekročiť. Odporúčame preto použiť \(64\)-bitové premenné, v jazyku C++ preto namiesto typu int použite typ long long int.
Formát výstupu
Variant A
Na jediný riadok výstupu vypíšte ano, ak sa v mriežke dá zostrojiť aspoň 47 rovnakých riadkov. V opačnom prípade vypíšte nie.
Variant B
Na jediný riadok výstupu vypíšte koľko najviac rovnakých riadkov sa dá zostrojiť zo zadaných magnetiek.
Hodnotenie
Úloha síce obsahuje 2 varianty, ale odovzdávanie bude fungovať štandardne. K úlohe sme pripravili \(5\) sád vstupov. Za vyriešenie každej sady získate 3 body. Tieto sady sa líšia veľkosťou vstupných údajov.
Ak sa rozhodnete riešiť Variant A, vaše riešenie bude otestované na prvých \(2\) sadách a môžete tak získať \(6\) bodov. Pri riešení Variantu B bude odovzdaný program otestovaný na všetkých \(5\) sadách, takže môžete získať \(15\) bodov. Interne testovanie vašich riešení funguje jednoduchým pravidlom. Ak je výstupom vášho programu číslo, testovač sa k nemu správa ako k riešeniu Variantu B. V opačnom prípade ho označí za riešenie Variantu A.
V nasledujúcej tabuľke označuje \(n\) veľkosť mriežky a \(r\) počet rôznych magnetiek. Vo vstupných sadách platí:
| Číslo sady | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| maximálne \(n\) | \(100\) | \(100\) | \(2\,000\) | \(50\,000\) | \(50\,000\) |
| maximálne \(r\) | \(300\) | \(500\) | \(2\,000\) | \(60\,000\) | \(60\,000\) |
Príklady
Variant B
Input:
4 5
3 6 1 4 2Output:
3Ide o príklad z úvodu pre mriežku \(4 \times 4\). Najviac vieme vytvoriť 3 rovnaké riadky, napríklad tak, ako je ukázané na druhom obrázku.
Input:
6 6
12 8 4 7 3 2Output:
4Vieme vytvoriť najviac \(4\) rovnaké riadky. Môžeme napríklad použiť 8 magnetiek prvého typu, 8 druhého, 4 tretieho a 4 štvrtého.
Variant A
Uvádzame ešte pár príkladov pre Variant A. Prvé dva príklady sú rovnaké ako pri Variante B.
Input:
4 5
3 6 1 4 2Output:
nieDajú sa vytvoriť najviac \(3\) rovnaké riadky, čo je menej ako 47, takže odpoveď je nie.
Input:
6 6
12 8 4 7 3 2Output:
nieOpäť vieme vytvoriť iba 4 rovnaké riadky, čo je menej ako 47 a odpovedáme nie.
Input:
60 6
537 690 108 395 193 1677Output:
anoV tomto príklade už vieme vytvoriť až \(57\) rovnakých riadkov, takže odpoveď je ano.
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.