5. Korytnačie preteky (vzorové riešenie)

Zadanie

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Žabovi na [email protected]

Medzi matfyzákmi sú Korytnačie preteky veľmi obľúbenou spoločenskou hrou a to napriek tomu, že táto hra je primárne určená pre päťročné deti. Pri prvom opise je totiž naozaj veľmi jednoduchá. Hrací plán pozostáva z niekoľkých za sebou idúcich políčok a cieľom hráčov je dostať korytnačku ich farby čo najrýchlejšie do cieľa. Korytnačky sa však môžu hýbať iba pomocou kariet, ktoré hráči na striedačku vykladajú. Každá karta určuje farbu korytnačky a počet políčok, o ktoré sa má korytnačka posunúť (tento počet môže byť aj záporný, vtedy ide korytnačka dozadu).

Toto znie pomerne priamočiaro. Akurát, hráči poznajú iba farbu svojej korytnačky, nevedia za ktorú korytnačku hrajú súperi a na ruke môžu mať karty ľubovoľnej farby. Navyše, korytnačky majú vskutku špecifický spôsob pohybu. Ak je totiž korytnačka presunutá na políčko, na ktorom sú iné korytnačky, nepostaví sa vedľa nich, ale na ne. Všetky korytnačky stojace na tom istom políčku teda vždy tvoria jeden stĺpik. Novú korytnačku, prichádzajúcu na políčko, vždy položíme na vrch stĺpika. A keď sa niektorá z korytnačiek tvoriacich stĺpik pohne, zoberie so sebou (presnejšie, na sebe) všetky na nej stojace korytnačky.

Pri hre naozaj často vznikajú takéto stĺpiky korytnačiek, ktoré sa spoločne presúvajú. Hráči sa snažia takticky držať svoje korytnačky na vrchu týchto kôpok (aby im ich posúvali aj ostatní hráči), a potom vo vhodnej chvíli rýchlo utiecť do cieľa.

Jano a Žaba sú vášniví hráči. Vytvorili si dokonca viacero hracích plánov, v ktorých je čoraz viac políčok aj korytnačiek. Nedávno ich pri hraní prišiel navštíviť Syseľ, drgol však do stola a rozsypal im všetky korytnačky. Jano a Žaba by chceli túto partiu dohrať. Našťastie si pamätajú všetky karty, ktoré postupne zahrali. Teraz by potrebovali rýchlo zistiť, aké bolo rozloženie korytnačiek v momente, keď prišiel Syseľ. Pomôžete im?

Úloha

Dostanete popis hry, ktorá sa odohrávala na \(p\) políčkach s \(n\) korytnačkami. Políčka sú očíslované od 1 po \(p\), pričom políčko 1 je začiatok a políčko \(p\) je cieľ. Korytnačky sú očíslované od 1 po \(n\). Na začiatku všetky korytnačky tvoria jeden stĺpik na políčku 1. Poradie korytnačiek v štartovacom stĺpiku dostanete zadané.

Následne sa odohralo \(q\) kariet. Každá karta určuje korytnačku, ktorá sa pohla, a počet políčok, o ktoré sa posunula dopredu. Toto číslo môže byť kladné aj záporné.

Vašou úlohou je zistiť, ako vyzerá hrací plán po odohratí všetkých zadaných kariet.

Formát vstupu

V prvom riadku vstupu sú tri čísla \(n\), \(p\) a \(q\) – počet korytnačiek, počet políčok a počet zahraných kariet.

V druhom riadku je \(n\) medzerou oddelených čísel udávajúcich začiatočné postavenie korytnačiek na políčku 1. Prvé číslo určuje číslo korytnačky na samom spodku stĺpika, druhé je číslo korytnačky priamo nad ňou a tak ďalej až po posledné číslo označujúce najvyššie položenú korytnačku. (Všetky tieto čísla sú od 1 po \(n\) a sú navzájom rôzne.)

Nasleduje \(q\) riadkov popisujúce karty v poradí, v akom boli zahrané. Každý z týchto riadkov sa skladá z troch čísel \(k_i\), \(p_i\) a \(x_i\). Tento riadok udáva, že korytnačka \(k_i\) pri zahratí tejto karty stála na políčku \(p_i\) a posunula sa o \(x_i\) políčok dopredu. (Záporné \(x_i\) teda v skutočnosti označuje pohyb dozadu.)

Zadaný vstup je korektný. Môžete teda predpokladať, že korytnačky skončia po každom pohybe na niektorom z políčok \(1\) až \(p\) a korytnačka \(k_i\) pri zahratí \(i\)-tej karty naozaj stojí na políčku \(p_i\).

Formát výstupu

Na výstup vypíšte \(p\) riadkov. V \(i\)-tom z týchto riadkov vypíšte popis korytnačiek na \(i\)-tom políčku. Prvé číslo riadku (označme ho \(x_i\)) udáva počet korytnačiek na tomto políčku. Zvyšok riadku má tvoriť ďalších \(x_i\) čísel: čísla korytnačiek na tomto políčku v poradí od spodku stĺpika po jeho vrch.

Hodnotenie

Váš program bude otestovaný na piatich vstupoch. Hodnoty \(n\), \(p\) a \(q\) v týchto vstupoch sú uvedené v tabuľke. Navyše, vo treťom vstupe platí, že každý presun korytnačky smeruje na prázdne políčko. V tomto vstupe sa teda nestane, že by sa korytnačka postavila na chrbát inej (stále však môžu cestovať v kôpke určenej z počiatočného rozostavenia).

Číslo vstupu	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(n\)	\(5\)	\(100\)	\(10\,000\)	\(100\,000\)	\(300\,000\)
\(p\)	\(20\)	\(1000\)	\(10\,000\)	\(1000\)	\(10\,000\)
\(q\)	\(25\)	\(1000\)	\(5\,000\,000\)	\(2\,000\,000\)	\(5\,000\,000\)

Príklad

Input:

Output:

Máme päť korytnačiek, sedem políčok a štyri zahrané karty. Na začiatku sú na políčku 1 korytnačky v poradí 2, 4, 1, 3, 5 zdola hore.

Potom sa postupne udeje nasledovné:

Korytnačka 1 sa z políčka 1 pohne o 3 dopredu, na políčko 4. Na chrbte so sebou odnesie aj korytnačky 3 a 5.
Korytnačka 3 sa z políčka 4 pohne o \(-3\) dopredu, teda naspäť na políčko 1. Na chrbte so sebou odnesie aj korytnačku 5. Na políčku 1 je teraz stĺpik 2, 4, 3, 5, zatiaľ čo na políčku 4 je samotná korytnačka 1.
Korytnačka 4 sa z políčka 1 pohne o 5 dopredu. Na políčku 1 zostane len korytnačka 2, ostatné korytnačky odnesie korytnačka 4 so sebou na políčko 6.
Korytnačka 1 sa zo svojho aktuálneho políčka 4 pohne o 2 dopredu a tam naskočí na vrch stĺpika.

Naprogramovať správne riešenie k tejto úlohe je pomerne jednoduché – stačí postupne simulovať jednotlivé kroky korytnačiek. Najjednoduchšie je vytvoriť si pre každé políčko hracieho plánu samostatné pole, v ktorom sú poukladané korytnačky v poradí, v akom stoja na danom políčku. Hodnoty na vstupe nám dokonca určujú, na ktorom políčku stojí korytnačka, ktorú presúvame, stačí preto z tohto poľa vybrať všetky korytnačky, ktoré sú nad ňou a v správnom poradí ich uložiť do cieľového políčka (teda to s číslom \(p_i + x_i\)).

Takéto riešenie avšak nie je efektívne. Môžeme však na ňom založiť rýchlejšie riešenie. Potrebujeme iba porozmýšľať, čo spôsobuje jeho neefektívnosť. Problémom samozrejme je, že pri simulovaní presúvame každú korytnačku samostatne a takýchto korytnačiek môže byť príliš veľa. Potrebovali by sme preto vymyslieť, ako nasimulovať to, čo vieme jednoducho spraviť v skutočnom živote – presunúť všetky korytnačky naraz.

Prvé riešenie si pre každú korytnačku v podstate pamätá, na ktorom políčku sa nachádza a táto informácia sa pri jednom presune naozaj zmení veľa korytnačkám. Aká informácia sa však pri jednom presune nezmení skoro žiadnej korytnačke? Predsa to, ktorá korytnačka sa nachádza priamo podomnou. Ked presúvame nejaký stĺpec korytnačiek, všetky okrem tej najspodnejšej ostanú sedieť na tej istej korytnačke a ich hodnota sa vôbec nemusí meniť. Na spracovanie jedného presunu preto stačí opraviť jednu hodnotu.

Navyše, túto informáciu na začiatku poznáme, sú ňou zadané hodnoty naskladaných korytnačiek a vieme pomocou nej vypočítať aj výsledok. Na konci totiž jednoducho prejdeme cez korytnačky a budeme sa posúvať vždy na nižšie ležiacu korytnačku, čím dostaneme jeden výsledný stĺpec.

Všímavý/á čitateľ/ka si však určite všimol/la jeden problém. Ako upravíme hodnotu presúvanej korytnačky? Ako vieme, na chrbát ktorej inej korytnačky sa postaví? Poprípade, čo ak na novom políčku ešte nie je žiadna korytnačka?

Pri každom presune sa korytnačka postaví navrch stĺpika na danom políčku. Pre každé políčko by sme preto chceli vedieť číslo najvyššej korytnačky, ktorá na ňom stojí. A v prípade, že tam žiadna korytnačka nestojí, môžeme si zapamätať napríklad hodnotu \(0\). Vieme však aj tieto hodnoty pri presune upravovať rovnako rýchlo?

Zoberme si dva stĺpiky korytnačiek na políčkach \(A\) a \(B\) a korytnačku \(x\), ktorú presúvame z \(A\) na vrch \(B\). Zmenia sa nasledovné tri hodnoty:

číslo korytnačky, na ktorej sedí korytnačka \(x\) – táto hodnota bude najvyššia korytnačka na políčku \(B\)
hodnota najvyššej korytnačky na políčku \(B\) – toto bude najvyššia korytnačka políčka \(A\), ktorá sa spolu s \(x\) presunula na vrch \(B\)
hodnota najvyššej korytnačky na políčku \(A\) – z políčka \(A\) sme odobrali všetky korytnačky, ktoré boli nad \(x\), najvyššie teda ostane korytnačka, na ktorej predtým sedela korytnačka \(x\)

Túto zmenu hodnôt pekne ilustruje nasledovný obrázok, v ktorom sa žlté korytnačky, ktoré sedeli na zelených posunuli na vrch modrých korytnačiek.

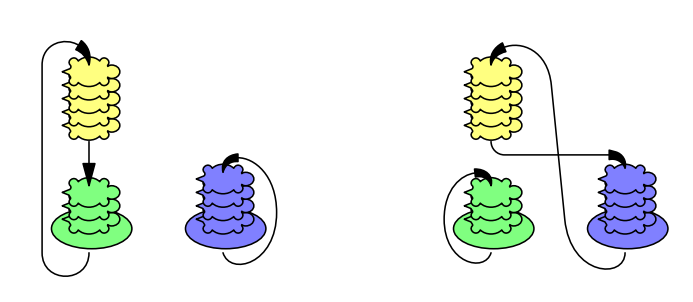
Pre každú korytnačku a políčko si teda stačí pamätať jedno číslo a pri každom presune zmeniť tri tieto čísla, čo vieme spraviť v konštantnom čase. Na konci sa jednoducho pre každé políčko pozrieme na najvyššiu korytnačku a z nej sa budeme posúvať dodola až kým nenarazíme na korytnačku, ktorá si pamätá, že nesedí na žiadnej korytnačke. Celková časová zložitosť takéhoto riešenia je \(O(n + p + q)\) a pamäťová zložitosť je \(O(n + p)\).

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

int main()
{
    int n, p, q;
    cin >> n >> p >> q;

    vector<int> podo_mnou(n + 1, 0); // kladna je koryt, 0 policko
    vector<int> vrchol(p + 1, 0);    // kladna je koryt, 0 nic

    int before = 0;
    for (size_t i = 0; i < n; ++i)
    {
        int kor;
        cin >> kor;
        podo_mnou[kor] = before;
        before = kor;
    }
    vrchol[1] = before;

    int k_i, p_i, x_i;
    while (cin >> k_i >> p_i >> x_i)
    {
        int old_vrchol = vrchol[p_i];
        int new_vrchol = vrchol[p_i + x_i];
        int pod = podo_mnou[k_i];

        vrchol[p_i] = pod;
        vrchol[p_i + x_i] = old_vrchol;

        podo_mnou[k_i] = new_vrchol;
    }

    for (size_t i = 1; i < vrchol.size(); ++i)
    {
        vector<int> out;

        int v = vrchol[i];
        while (v != 0)
        {
            out.push_back(v);
            v = podo_mnou[v];
        }

        reverse(out.begin(), out.end());

        cout << out.size();
        for (int kor : out)
            cout << " " << kor;
        cout << "\n";
    }
}

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.

5. Korytnačie preteky vzorové riešenie