2. Rebríky a Platformy vzorové riešenie

Zadanie

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Paulinke na [email protected]

Jedného pekného letného dňa sa Adrianka vybrala do novučičkého Parku Rebríkov a Spúšťacích Kladiek a celé hodiny skúšala rôzne rebríky, lanové dráhy a iné atrakcie. Už od príchodu so zvedavým pohľadom obdivne hľadela na najväčšiu a najkomplikovanejšiu sústavu lanorebríkov akú Park Rebríkov a Spúšťacích Kladiek mal v ponuke.

Starostlivo si vyhliadla moment, keď bol rad ku komplexu najkratší, a hneď sa do neho postavila. Rad pomaličky ubúdal a Adrianka z nudy začala analyzovať ten komplexný systém platforiem pospájaných dokopy rebríkmi z lán.

Celá preliezka sa skladala z radu za sebou idúcich platforiem umiestnených v rôznych výškach. Každé dve za sebou idúce platformi boli spojené lanorebríkom, po ktorom sa človek posúval ďalej. Tento lanorebrík buď stúpal alebo klesal v závislosti od vzájomnej výšky platforiem, ktoré spájal. Adrianka si navyše všimla veľmi zaujímavú vlastnosť – žiadne dve platfotmy neboli v rovnakej výške. V propagačnej brožúrke sa dokonca dočítala, že pre každú výšku v metroch od 1 po počet platforiem existuje platforma v danej výške.

Rad sa viac a viac skracoval a čoskoro mala na dráhu nastúpiť aj Adrianka. Zrazu si pri nástupnej plošine všimla plagát: “Uhádni výšky plošín a vyhraj!” Adrianka však pohľadom na plošiny nevedela odhadnúť ako vysoko sú. Počas presunu si teda dôkladne zapamätala aspoň to, na ktorých úsekoch dráhy stúpala, a na ktorých klesala, v nádeji, že jej to pomôže pri odhade.

Pomôžte jej zo získaných dát zistiť možné výšky platforiem!

Príklad

Ak by prvý úsek išiel dole, druhý hore a tretí opäť dole, výška platforiem (v metroch) by mohla byť 4, 1, 3, 2. Rovnako dobré by však bolo aj riešenie 2, 1, 4, 3.

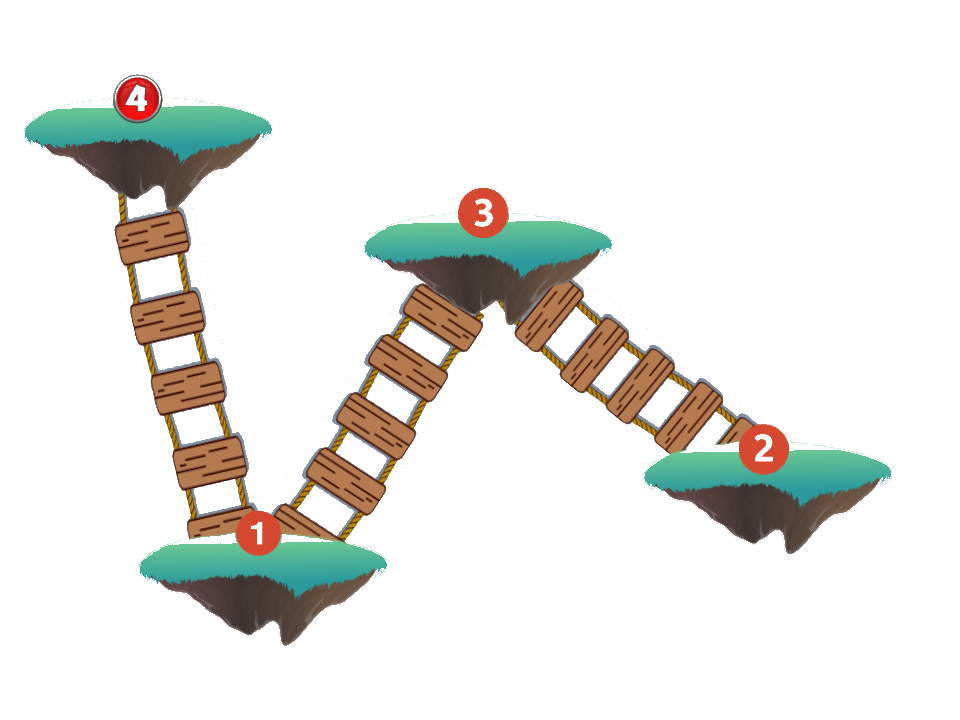
Stúpanie a klesanie vieme zaznačiť schematicky: \(\uparrow\) značí stúpanie, \(\downarrow\) klesanie. Napríklad táto lanorebríková sústava sa dá zaznačiť ako \(\downarrow\uparrow\downarrow\)

Úloha

1. (2 body) Pre každú z troch zadaných postupností klesaní a stúpaní nájdite jedno možné rozloženie výšok platforiem, ktoré by mohlo zodpovedať zadanej postupnosti:
   • \(\downarrow\downarrow\uparrow\downarrow\uparrow\) (hľadáte postupnosť 6 platforiem s rôznymi výškami od 1 po 6)
   • \(\downarrow\downarrow\uparrow\uparrow\) (hľadáte postupnosť 5 platforiem s rôznymi výškami od 1 po 5)
   • \(\downarrow\downarrow\uparrow\uparrow\uparrow\uparrow\downarrow\downarrow\downarrow\uparrow\uparrow\) (hľadáte postupnosť 12 platforiem s rôznymi výškami od 1 po 12)

2. (2 body) Adrianka si povedala, že sa uspokojí aj s tým, keď nájde plošinu, ktorá by mohla byť vo výške 1. Popíšte postup, ktorý pre ľubovoľnú postupnosť stúpaní a klesaní nájde jednu pozíciu pre platformu s výškou 1. Možných pozícii môže byť viac, v takom prípade stačí ak nájdete ľubovoľnú jednu z nich.

   Vami navrhnutý postup si môžete otestovať na príkladoch z podúlohy a).

3. (4 body) Navrhnite postup, ktorý pre ľubovoľnú postupnosť stúpaní a klesaní nájde jedno možné priradenie výšok platformám, ktoré spĺňa podmienky zadania.

   Vaše riešenie má teda robiť niečo podobné ako ste vy robili v podúlohe a), preto si to na daných postupnostiach môžete vyskúšať. Pozor však na to, že musí fungovať aj pre iné, aj oveľa dlhšie postupnosti. Na overenie správnosti si môžete vytvoriť vlastné postupnosti a skúsiť to aj na nich.

4. (3 body) Na konci dráhy sa Adrianka dozvedela, že cenu útechy dostane aspoň za to, keď uhádne výšku prvej platformy. Rozmýšľa teda, koľko rôznych vyšok je pre túto platformu prípustných. Popíšte, ako by ste pre ľubovoľnú postupnosť stúpaní a klesaní určili, ako rôzne vysoko môže byť prvá platforma.

   Ak neviete ako túto podúlohu vyriešiť všeobecne, až 1 bod môžete získať ak ju vyriešite na troch konkrétnych príkladoch z podúlohy a).

5. (4 body) Adrianka sa od manažérky dráhy dozvedela, že lanová dráha je postavená tak, aby bola čo najadrenalínovejšia. To sa prejavuje tak, že na začiatok dráhy sú umiestňované čo najvyššie platformy. Ak mali návrhári dráhy viac možností (dodržiac všetky predchádzajúce podmienky vrátane dopredu stanoveného stúpania a klesania) ako umiestniť platformy, vybrali si tú, kde bola prvá platforma čo najvyššia. Ak mali stále viac možností, snažili sa maximalizovať výšku druhej, tretej atď. platformy. Inak povedané, vybrali si lexikograficky najväčšiu vyhovujúcu postupnosť.

   Adrianka je presvedčená, že s prihliadnutím na túto podmienku existuje iba jedno riešenie zhodujúce sa s dátami ktoré namerala. Pomôžte jej a navrhnite postup, ktorý pre ľubovoľnú postupnosť stúpaní a klesaní nájde najadrenalínovejšiu lanovú dráhu.

   Ako by niečo takéto vyzeralo pre postupnosť z obrázku, teda \(\downarrow\uparrow\downarrow\uparrow\)? Na prvé miesto by išla platforma výšky 4. Stále sú však prípustné dve možnosti – (4, 1, 3, 2) a (4, 2, 3, 1). Vybrať musíme tú druhú, lebo má vyššie umiestnenú druhú platformu.

V prvých dvoch podúlochách ste si mohli vyskúšať ako riešiť úlohu manuálne, a potom toto riešenie zovšeobecniť pre ľubovoľnú zadanú postupnosť stúpaní a klesaní.

Podúloha (a)

• Príklad takejto postupnosti môže byť napríklad 4, 3, 1, 5, 2, 6. Všimnite si, že rovnako dobré by bolo riešenie 4, 3, 1, 6, 2, 5, či 5, 3, 1, 4, 2, 6.

• Všimnite si, že tu musí byť stredná platforma vo výške 1, pretože všetky ostatné platformy sú od nej nižšie. Pre ostatné už máme viac možností, napríklad 3, 2, 1, 4, 5, či 5, 4, 1, 2, 3.

• Tu riešením môže byť napríklad 3,2,1,4,5,6,12,11,10,7,8,9

Podúloha (b)

Prvé pozorovanie je, že jednotkovú výšku môžu mať iba platformy z ktorých idú oba (prípadne len jeden, ak to je koncová platforma) rebríky hore.

Platí však, že každá takáto platforma môže mať výšku jedna?

Predstavme si že nastavíme výšku tejto platformy na jedna. Teraz sa nám dráha rozdelí na dve časti (časť môže byť aj prázdna). Všimnime si, že nech sú vedľajšie platformy akejkoľvek zostávajúcej výšky (teda výsky od dva do počtu platforiem), tak nerovnosť s najnižšou platformou stále platí!

Teraz si vieme povedať, že do jednej časi dráhy (napríklad tej naľavo od najnižšej platformy) dáme výšky od 2 do \(2+n\) (kde \(n\) je počet platforiem naľavo od nás) a do pravej tie zvyšné. Takto sa nám problém rozpadne na dva podproblémy, a ak vždy existuje riešenie (ako ukážeme, existuje), jednotka na danom mieste môže byť.

Podúloha (c)

Predchádzajúca podúloha nám povedala ako na to: nájdime ľubovoľnú platformu ktorá môže mať výšku jedna. Potom sa pozrime na platformy naľavo od nej. Ak tam už nie sú žiadne, zopakujeme nasledovný proces pre pravú stranu:

Znova zopakujeme postup: nájdeme platformu ktorá môže mať výšku dva. To je ľubovoľná z ktorej idú všetky (jeden alebo dva) rebríky hore, pričom sa tvárime že rebrík na platformu jedna neexistuje (vieme, že nech bude výška susediacej platformy ľubovoľná z 2 až po počet platforiem, nerovnosť je vždy splnená). Teraz zase rozdelíme stranu na dve časti a ak je niektorá z nich neprázdna opakujeme tento postup.

Keď sme skončili ľavú stranu, opakujme pre pravú stranu.

Pre ilustráciu sa pozrime na podúlohu (a), tretiu dráhu:

Tretia platforma môže byť najnižšie, takže nech má výšku jedna. Potom máme \(\downarrow\downarrow\) na ľavej strane, takže platforma s výškou dva musí z týchto dvoch byť tá druhá a prvá platforma má tak výšku 3.

Dokončili sme ľavú stranu, pozrime sa na pravú. Hneď krajná (štvrtá platforma) môže mať výšku \(4\). Potom piata má zas len rebrík hore, takže môže mať výšku \(5\) a podobne šiesta môže mať výšku \(6\).

Zo siedmej už ide rebrík dole, tak musíme hľadať ďalej. Jediné miesto, kde vieme umiestniť výšku \(7\) je teraz desiata platforma. Platformy naľavo od nej postupne (v poradí siedma, ôsma, deviata) dostanú výšky 10, 9 a 8.

A napokon, posledné dve platformy skončia s výškami 11 a 12, a teda výsledné výšky sú 3,2,1,4,5,6,10,9,8,7,11,12.

Podúloha (d)

Ako vysoko môže byť prvá platforma? Môže byť vo výške 1? Ak z nej nejde rebrík dole, potom áno (ako sme ukázali v podúlohe (b)). Čo ak z nej ide dole za sebou \(k\) rebríkov? Potom môže byť najnižšie vo výške \(k+1\) – nasledujúce platformy musia byť postupne vo výškach \(k\), \(k - 1\), atď. až po \(1\). Potom si zvyšok platformy vieme predstaviť ako separátnu dráhu, do ktorej umiestňujeme výšky \(k+1\) až po počet platforiem.

Podobne sa môžeme pýtať, či môže byť prvá platforma vo výške \(n\). Tiež platí, že ak prvých \(k\) rebríkov ide hore, môže byť prvá platforma vo výške nanajvýš \(n-k\).

Čo s ostatnými výškami?

Bez ujmy na všeobecnosti, nech ako prvé ide \(k\) rebríkov dole. Dajme prvú platformu do ľubovoľnej výšky aspoň \(k + 1\) a ďalšie \(k\) platformy budú postupne \(k\), \(k - 1\), atď až po \(1\). Potom akúkoľvek výšku bude mať nasledovná platforma, tak nerovnosť bude platiť (keďže sme výšku jedna umiestnili tak kde môže byť). Potom nám vlastne vznikol separátny problém s \(n - k - 1\) platformami, ktorý určite vieme algoritmom z úlohy (c) vyriešiť.

Takže akákoľvek výška \(> k\) pre prvú platformu funguje. Rovnako, keď z prvej platformy ide \(k\) rebríkov hore, na platforme jedna môže byť akákoľvek výška \(\leq n - k\).

Podúloha (e)

Z podúlohy (d) vieme, akú najvyššiu výšku vieme dať na prvú platformu.

Najskôr sa pozrime na prípad, že prvý rebrík ide dole. Vtedy je najvyššia platforma hneď na začiatku. Potom keď sa pozrieme na zvyšné platformy, dostaneme rovnaký problém ako predtým, len o jednu platformu kratší.

Ak ide z prvej platformy \(k\) rebríkov po sebe hore, potom najvyššie ako vie byť prvá platforma je \(n - k\), a nasledujúce platformy musia byť \(n - k + 1\), \(n - k + 2\), \(\dots\), \(n\). Ďalšia platforma musí byť nižšia – dostali sme menší problém s \(n-k-1\) platformami.

Ako tento algoritmus funguje si ukážme znova na poslednom príklade z podúlohy (a):

Máme dvanásť platforiem. Prvé dva rebríky idú dole, takže najvyššie ako vieme položiť prvé dve platformy sú postupne 12 a 11 metrov. Ďalšie štyri rebríky idú hore, takže ďalších päť platforiem je vo výškach postupne \(6\), \(7\), \(8\), \(9\) a \(10\) metrov. Ďalšie tri rebríky idú dole, takže najväčšie možné výšky ďalších troch platforiem sú \(5\), \(4\) a \(3\). A napokon, posledné dva rebríky smerujú hore, takže posledné dva rebríky musia byť \(1\) a \(2\).