1. Poskakujúci Super Mário vzorové riešenie

Zadanie

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Romanovi na [email protected]

Super Mário spokojne prežíval jeden zo svojich troch životov – jedol hríby, poskakoval medzi stromami, a naháňal sa za princeznou. Pri jednom skoku sa ale pošmykol a spadol do veľkej zelenej rúry. Keď precitol, zistil, že sa nachádza v nevedno akom veľkom systéme miestností.

Tento systém je tvorený niekoľkými navzájom nerozoznateľnými miestnosťami usporiadanými do kruhu. Z každej miestnosti vedú dve prechodové komory do susedných miestností. Okrem toho je tam už len jedno stropné svetlo a vypínač, ktoré toto svetlo ovláda. Pomocou neho vie Mário v danej miestnosti vypnúť alebo zhasnúť svetlo.

Na obrázku nižšie je jednoduchý systém so štyrmi miestnosťami. Mário sa nachádza v hornej z nich a v miestnosti je aktuálne zhasnuté.

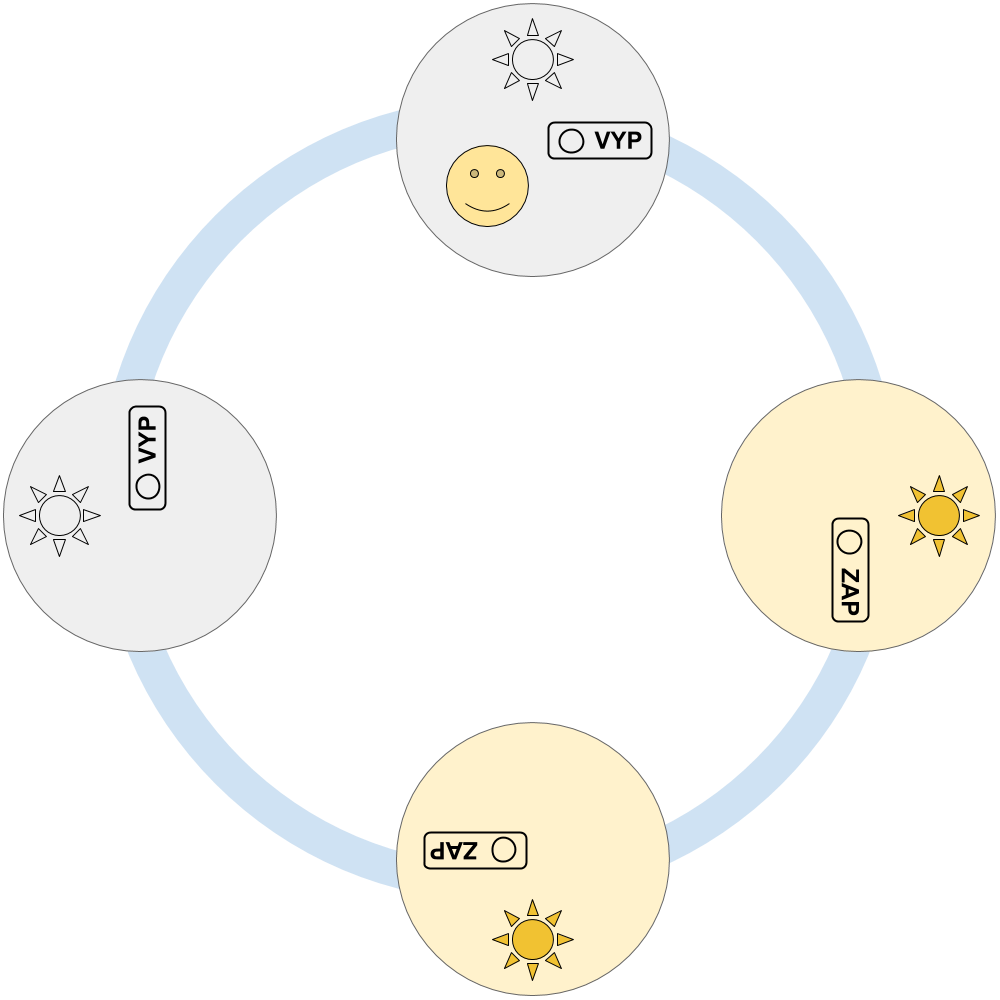
Mário by rád zistil, v akom rozsiahlom systéme sa nachádza, teda určil počet miestností, ktoré ho tvoria. Má však niekoľko problémov. Síce zapnutie a vypnutie svetiel ovláda iba Mário pomocou vypínačov v miestnosti, netuší ako sú tieto svetlá rozsvietené na začiatku. V niektorých miestnostiach sú zapálené, v iných nie. No najmä, napriek tomu že je Super, si nevie v miestnostiach nechávať žiadne značky ani ich iným spôsobom označovať. Je teda naozaj odkázaný iba na zapínanie a vypínanie svetiel.

Úloha

Mário môže robiť dva typy akcií: prechádzať dverami medzi skrýšami a rozsvecovať alebo zhasínať svetlo v jednotlivých skrýšach. Vašou úlohou je pomôcť mu s nasledujúcimi problémami.

1. (2 body) Vymyslite spôsob, ktorým Mário zistí, či je v systéme práve jedna miestnosť alebo ich je viac. Ak je systém miestností tvorený iba jednou miestnosťou, tak jediná prechodová komora spája jedny jej dvere s druhými. Ak teda Mário opustí miestnosť jedným koncom, vojde druhým koncom do tej istej miestnosti.

2. (3 body) Nájdite ľubovoľný spôsob, ktorým Mário zistí, či sú miestnosti aspoň tri.

3. (6 body) Nájdite ľubovoľný postup, ktorým vie Mário zistiť počet miestností v systéme, bez ohľadu na to, aký je veľký.

4. (4 body) Označme si počet miestností v systéme ako \(n\) (ktoré Mário stále nepozná). Nájdite taký spôsob na určenie tejto hodnoty, pri ktorom Máriovi stačí spraviť nanajvýš \(20n + 47\) akcií (táto hodnota výrazne prevyšuje počet akcií, ktoré potrebuje spraviť vzorové riešenie). Odôvodnite, prečo váš postup nepotrebuje viac akcií.

   Ak si nie ste istý, koľko otázok používa váš postup, aj tak nám ho pošlite, určite získate aspoň čiastkové body :)

Prvé dve podúlohy sú vlastne návodom k riešenie tretej, hlavnej podúlohy. Prejdeme si preto detailne cez prvú podúlohu a potom rovno ukážeme všeobecné riešenie tretej. Vo všetkých riešeniach budeme dva smery pohybu pre jednoduchosť volať “doprava” a “doľava”, netreba však zabúdať, že stanica je cyklická – teda keď Mário pôjde dostatočne dlho “doprava”, dostane sa určite na miesto, kde začínal.

Podúloha A: je miestnosť jedna?

Jediná vec, ktorú vie Mário použiť na rozlíšenie miestností, je svetlo. Ako ale spoznať, či je to naozaj nová miestnosť a nie iná, v ktorej je tiež zasvietené?

Trik spočíva v tom, že ak ide o dve rôzne miestnosti, prepnutie svetla v jednej z nich sa neprejaví v druhej. Keď si toto uvedomíme, už ľahko vymyslíme spôsob kontroly. Jedno možné riešenie vyzerá nasledovne:

1. rozsvieť
2. pohni sa doprava
3. ak tam je zhasnuté, je to iná miestnosť, a teda sú aspoň dve, koniec
4. ak tam je rozsvietené, zhasni
5. pohni sa naspäť doľava
6. ak je tam zrazu zhasnuté, muselo ísť o tú istú miestnosť, a teda je len jedna, koniec
7. ak v prvej miestnosti ostalo rozsvietené, sú aspoň dve miestnosti, koniec

Podúlohy B a C: koľko je miestností?

Jedno možné všeobecné riešenie podúlohy C bude vyzerať tak, že postupne otestujeme, či sú miestnosti aspoň dve (to už vieme robiť), či sú aspoň tri, aspoň štyri, a tak ďalej. Akonáhle takýto test prvýkrát zlyhá, budeme presne vedieť, koľko miestností má náš systém.

Teraz si rozmyslíme, ako skontrolovať, či je miestností aspoň \(k\). Postup bude zovšeobecnením toho z podúlohy A: najskôr dostatočne veľa miestnosti v rade rozsvietime a potom sa pozrieme, čo sa stane, keď ich pôjdeme postupne zhášať. Ukážeme si najskôr samotné riešenie:

1. rozsvieť v miestnosti, kde začínaš
2. (k-1)-krát sa posuň doprava a rozsvieť aj tam (ak bolo zhasnuté)
3. zhasni v miestnosti, kde práve si
4. (k-1)-krát sprav nasledovné:
        posuň sa naspäť doľava
        ak si prišiel/a do miestnosti, kde je zhasnuté, miestností je menej ako k, koniec
        zhasni v miestnosti, kde práve si
5. ak si sa dostal/a až sem, miestností bolo aspoň k

Prečo toto riešenie funguje? Rozmyslime si, čo sa stane, ak máme miestností aspoň \(k\) a čo sa stane, ak ich je menej. Ak máme miestností aspoň \(k\), v prvých dvoch krokoch postupne navštívime \(k\) rôznych miestností a v každej z nich rozsvietime, a potom v krokoch 3 a 4 cez ne prejdeme naspäť a v každej zhasneme. Všetko zafunguje ako má a dáme správnu odpoveď.

Ak máme miestností menej ako \(k\), niekedy počas kroku 2 sa “zacyklíme” – teda prídeme znova do miestnosti, v ktorej sme už boli. Špeciálne teda aj miestnosť, v ktorej skončíme krok 2, sme určite navštívili (aspoň) dvakrát. V kroku 3 v nej zhasneme. Ale potom keď sa v kroku 4 vraciame naspäť, určite sa ešte (aspoň) raz do tejto miestnosti vrátime. No a keď sa tak stane, uvidíme, že v nej už je zhasnuté a z toho vieme, že sme v nej už boli, a teda že miestností musí byť menej ako \(k\).

Podúloha D: efektívne riešenie

Koľko zhruba krokov urobí Mário pri predchádzajúcom riešení? Ak je skutočný počet miestností \(n\), Mário postupne spraví 1 krok doprava, 1 doľava, 2 doprava, 2 doľava, \(\dots\), až nakoniec \(n\) doprava a potom \(n\) doľava. Dokopy teda spraví rádovo \(n^2\) krokov (a rádovo toľko isto prepnutí svetla).

Ako vieme tento postup urýchliť? Všimnime si, čo sa stane, ak použijeme ten istý postup, len nebudeme skúšanú veľkosť miestnosti zväčšovať vždy o 1, ale rýchlejšie. Napríklad sa zamyslime, čo sa stane, keď vyššie popísaný postup použijeme pre \(k = 10\), ale miestností je len 7. V krokoch 1 a 2 postupne navštívime 10 miestností a v každej zažneme. V krokoch 3 a 4 sa nám potom ale podarí zhasnúť len 7-krát (lebo len toľko miestností naozaj máme) a po nasledujúcom pohybe už nájdeme v miestnosti tmu.

Ak teda použijeme vyššie použitý postup a budeme si navyše počítať, v koľkých miestnostiach sa nám naozaj podarilo zhasnúť, vieme presne povedať, či bola miestnosť len jedna, či boli presne dve, presne tri, \(\dots\), či ich bolo presne \(k - 1\) alebo či ich muselo byť aspoň \(k\). No a po tomto vylepšení už môžeme skúšať len niektoré vhodne zvolené hodnoty \(k\).

Celé riešenie teda bude vyzerať napríklad tak, že vyššie popísaným postupom budeme postupne zisťovať presný počet miestností ak je menší ako 2, ak je menší ako 4, potom 8, 16, 32, a tak ďalej. (Rovnako dobre sme mohli použiť napríklad mocniny 10, alebo inú postupnosť ktorá rastie exponenciálne.)

Prečo má tento postup lepšiu časovú zložitosť? Počítajme. V poslednom kole (v tom, kedy už odhalíme správny počet miestností) prejdeme celý systém nanajvýš dvakrát smerom tam a presne raz smerom späť. V predposlednom kole prejdeme nanajvýš celý systém tam a späť. O kolo skôr to už muselo byť nanajvýš pol systému tam a späť, predtým štvrtina, a tak ďalej. No a keď toto celé spočítame, dostaneme, že dokopy spravíme nanajvýš \(7n\) krokov. A keďže každému kroku zodpovedá najviac jedno prepnutie svetla, je aj tých len lineárne veľa – a teda celé toto riešenie má časovú zložitosť lineárnu od počtu miestností v stanici.

Formálne, k ľubovoľnému \(n\) vieme nájsť \(t\) také, že \(2^{t−1} \leq n < 2^t\). Pre toto \(n\) spraví vyššie popísaný algoritmus postupne \(t\) kontrol, pričom bude postupne voliť \(k = 2^1, 2^2, \dots, 2^t\). Počas týchto kontrol spraví menej ako \(2^1 + 2^2 + \dots + 2^t < 2^{t+1}\) krokov smerom doprava a menej ako \(2^1 + 2^2 + \dots + 2^{t−1} + n < 2^t + n\) krokov smerom doľava. Dokopy teda spraví menej ako \(2^{t+1} + 2^t + n = 6 \cdot 2^{t−1} + n \leq 6n + n = 7n\) krokov.