Zadanie
Ak nevieš programovať, nezúfaj! Môžeš sa to naučiť a ešte za to získať body, ktoré sa ti budú počítať namiesto tejto úlohy.
Stačí, že pôjdeš na stránku Programátorskej Liahne (liahen.ksp.sk). Keď budeš riešiť sadu conditions_cpp, bodmi, ktoré získaš si môžeš nahradiť riešenie tejto úlohy. Stačí ak na spodku tejto stránky odovzdáš pdf-ko s prezývkou, ktorú používaš na Liahni.
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Danovi na [email protected]
Farmár Fero nie je farmár. Ale chcel by byť. Na to však, samozrejme, potrebuje pole. Blízko jeho domu je veľký kus hospodárskej pôdy, ktorú nikto nevyužíva. Je ako stvorená pre neho. Keď ale Fero zistil tú strašnú cenu za každý meter štvorcový tejto pôdy, uvedomil si, že si môže dovoliť odkúpiť iba nejaký menší kúsok.
Celá hospodárska pôda má štvorcový tvar. Fero by z nej chcel nejaký obdĺžnik. Prečo zrovna obdĺžnik? Keby to bol nejaký krivoľaký útvar, ťažko by sa mu na ňom manévrovalo s kombajnom. A on na tom poli predsa nič iné robiť nebude.
Hospodárska pôda je naozaj rozsiahla. Je to štvorec rozmerov \(n \times n\) metrov. Niektoré jej časti sú úrodnejšie, ako iné. Terajší vlastník má pre každé políčko veľkosti \(1 \times 1\) meter spočítané, ako veľmi je úrodné. Na niektorých políčkach neprežije ani burina, na iných vie vyrásť aj kukurica. Nájdu sa dokonca aj tak neúrodné políčka, že im terajší vlastník priradil zápornú hodnotu. Všetky tieto dáta poskytol Ferovi. Vraj aby sa mohol dobre rozhodnúť.
Náš odhodlaný takmer-farmár začal hútať, ktorý obdĺžnik by si mal vybrať, aby bol čo najúrodnejší. Vytipoval si niekoľko kandidátov. Teraz ale pre každý z vytipovaných obdĺžnikov potrebuje vedieť, aká je jeho úrodnosť. Pomôžete mu vybrať jeho pole?
Úloha
Kus hospodárskej pôdy má rozmery \(n \times n\) metrov. Je tvorený políčkami rozmerov \(1 \times 1\) meter. Ide teda o akúsi mriežku s \(n\) riadkami a \(n\) stĺpcami. Pre každé políčko poznáte jeho úrodnosť vyjadrenú celým číslom. Fero sa vás opýta \(q\) otázok. Každá otázka predstavuje obdĺžnik na veľkom kuse hospodárskej pôdy. Pre každý takýto obdĺžnik je vašou úlohou spočítať súčet úrodností jeho políčok.
Formát vstupu
Na prvom riadku vstupu je číslo \(n\). To hovorí, že kus hospodárskej pôdy, z ktorej si Fero ide vyberať obdĺžnikové pole, má rozmery \(n \times n\) políčok. Platí, že \(1 \leq n \leq 2\,000\).
Nasleduje \(n\) riadkov. V každom z nich je \(n\) čísel. Číslo \(x_{ij}\) v \(i\)-tom riadku a \(j\)-tom stĺpci hovorí, že políčko v \(i\)-tom riadku a \(j\)-tom stĺpci hospodárskej pôdy má úrodnosť \(x_{ij}\). Platí, že \(-1\,000 \leq x_{ij} \leq 1\,000\).
Na ďalšom riadku je číslo \(q\) – počet otázok. Môžete predpokladať, že \(1 \leq q \leq 100\,000\).
Nasleduje \(q\) riadkov – jednotlivé otázky. Každý riadok obsahuje \(4\) čísla \(r_1\), \(c_1\), \(r_2\), \(c_2\). Odpoveďou na túto otázku je úrodnosť obdĺžniku, ktorý má ľavý horný roh v riadku \(r_1\) a stĺpci \(c_1\), a pravý dolný roh v riadku \(r_2\) a stĺpci \(c_2\). Platí, že \(0 \leq r_1, c_1, r_2, c_2 \leq n - 1\) a tiež, že \(r_1 \leq r_2\) a \(c_1 \leq c_2\).
Formát výstupu
Pre každú otázku vypíšte jej odpoveď na jeden riadok. Odpovede vypisujte v takom poradí, v akom ste dostali otázky. To znamená, že v prvom riadku bude odpoveď na prvú otázku, v druhom na druhú, atď.
Hodnotenie
Sú 3 sady vstupov. Platia pre ne nasledové horné obmedzenia pre hodnotu \(q\).
| Číslo sady | 1 | 2 | 3 |
|---|---|---|---|
| \(q \leq\) | \(10\) | \(10\,000\) | \(100\,000\) |
Príklad
Input:
4
1 -2 -3 4
-2 4 -1 2
1 -2 3 5
0 -1 9 9
2
1 1 2 3
1 3 1 3Output:
11
2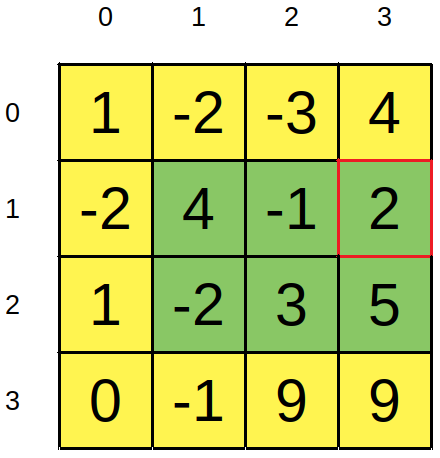
Zjednodušene povedané, na vstupe sme dostali mriežku čísiel a niekoľko obdĺžnikových plôch na tejto mriežke. Našou úlohou bolo pre každú zadanú obdĺžnikovú plochu zrátať súčet čísiel na nej.
Priamočiare riešenie
Prvé, čo by nám malo napadnúť je, že každý zadaný obdĺžnik prejdeme políčko po políčku a takto si ho celý nasčítame.
Každný obdĺžnik teda spracujeme v \(O(n^2)\) a obdĺžnikov bolo \(q\), takže časová zložitosť tohto riešenia je \(O(qn^2)\). Pamätáme si iba mriežku, takže pamäť bude \(O(n^2)\).
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2001;
int rola[MAXN][MAXN];
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); // rychle nacitavanie vstupu
int n;
cin >> n;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
cin >> rola[i][j];
int q, r1, c1, r2, c2;
cin >> q;
while(q--) {
long long odpoved = 0;
cin >> r1 >> c1 >> r2 >> c2;
for(int r = r1; r <= r2; r++)
for(int c = c1; c <= c2; c++)
odpoved += rola[r][c];
cout << odpoved << '\n';
}
return 0;
}Zrýchlenie
Využijeme známy trik známy ako prefixové súčty, alebo prefixové sumy. V čom spočíva? To sa dozviete v tomto článku v KSP kuchárke.
Keď už vieme, čo sú to prefixové súčty, tak by nemal byť problém použiť ich na riešenie tejto úlohy.
Zrátame si prefixové súčty pre každý riadok mriežky samostatne. Keď teraz chceme zistiť výsledok pre nejaký obdĺžnik, tak nemusíme prechádzať všetky jeho políčka. Stačí nám prejsť všetky jeho riadky. Pre každý jeho riadok totiž z prefixových súčtov vieme zrátať, koľko daný riadok pridá ku súčtu.
Ako sme si pomohli? Každý obdĺžnik teraz už vieme spočítať v čase \(O(n)\). Zrátanie prefixových súčtov nám dokopy na začiatku zaberie čas \(O(n^2)\). Obdĺžnikov je stále \(q\), takže celkovo sme čas zlepšili na \(O(n^2 + qn)\). Pamäť nemáme ako zlepšovať, je stále \(O(n^2)\).
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2001;
int rola[MAXN][MAXN];
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); // rychle nacitavanie vstupu
int n;
cin >> n;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
cin >> rola[i][j];
// Zratame prefixove sucty pre kazdy riadok
for(int i = 0; i < n; i++)
for(int j = 1; j < n; j++)
rola[i][j] += rola[i][j - 1];
int q, r1, c1, r2, c2;
cin >> q;
while(q--) {
long long odpoved = 0;
cin >> r1 >> c1 >> r2 >> c2;
for(int r = r1; r <= r2; r++) {
odpoved += rola[r][c2]; // pripocitame prefix riadku az po koniec obdlznika
if(c1 > 0)
odpoved -= rola[r][c1 - 1]; // odpocitame prefix riadku, ktory este nepatri do obdlznika
}
cout << odpoved << '\n';
}
return 0;
}Vzorové riešenie
Od predchádzajúcej myšlienky už ku vzorovému riešeniu nechýba veľa. Stačí myšlienku prefixových súčtov rozšíriť do dvoch rozmerov. Môžete si skúsiť vymyslieť, ako by to mohlo fungovať. Ak sa vám nechce vymýšľať, môžete si prečítať článok o 2D prefixových súčtoch z KSP kuchárky.
Vzorové riešenie tejto úlohy je potom už jednoduché. Na mriežke si zrátame 2D prefixové súčty a na každú otázku potom budeme vedieť odpovedať v \(O(1)\). Zrátanie 2D prefixových súčtov nám bude trvať \(O(n^2)\). Celkový čas teda bude \(O(n^2 + q)\). Pamäť ostane \(O(n^2)\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.