1. Poskakujúci kôň vzorové riešenie

Zadanie

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Romanovi na [email protected]

Emovi sa končila stáž v Zurichu a potreboval pred odchodom upratať byt. Po chvíli upratovania našiel v kope neporiadku niečo zaujímavé – nekonečnú¹ šachovnicu a figúrku jazdca (koňa). Emo si síce uvedomoval, že by mal upratovať, no napriek tomu si sadol k šachovnici a začal sa s jazdcom hrať. Však len chvíľku…

Ale chvíľa sa natiahla a Emo si zrazu uvedomil, že ak v okamihu neodíde, zmešká lietadlo. Čo však s nevyriešenými problémami, ktoré mu pri hraní napadli?

Úloha

Každému políčku Emovej nekonečnej šachovnice vieme priradiť dvojicu čísel, ktoré určujú jeho súradnice. Prvé číslo zodpovedá horizontálnej (stĺpec) a druhé vertikálnej (riadok) pozícii vzhľadom na začiatok \((0,0)\). Zopár príkladov súradníc nájdete na obrázku nižšie.

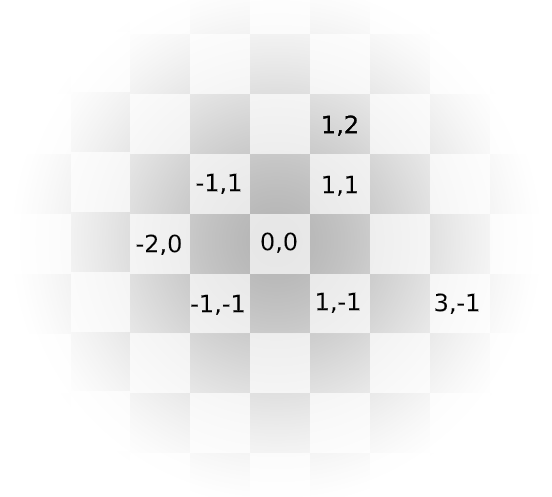
Na začiatku stojí na políčku \((0,0)\) jazdec, ktorý sa môže pohybovať podľa štandardných šachových pravidiel. Pohyb jazdca pripomína písmeno L – najskôr sa posunie o dve políčka v zvislom alebo vodorovnom smere a potom ešte o jedno políčko kolmo na pôvodný smer. Na nekonečnej šachovnici má teda pri každom skoku na výber osem políčok, na ktoré sa môže presunúť (viď obrázok).

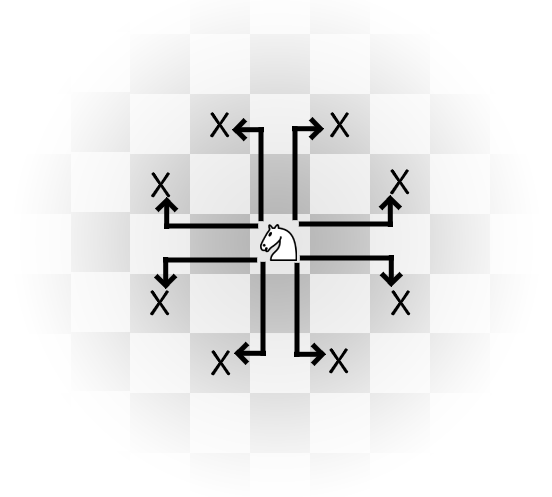
1. (2 body) Políčko \((0,0)\) má bielu farbu a zvyšené políčka sú ofarbené šachovnicovo. Akú farbu bude mať políčko, na ktoré sa jazdec dostane po \(X\) skokoch? Prečo?

2. (2 body) Jazdec zo svojho začiatočného políčka urobil presne dva skoky. Na koľkých rôznych políčkach môže teraz stáť? Aké súradnice majú tieto políčka?

3. (2 body) Koľko najmenej skokov potrebuje jazdec na to, aby sa dostal zo svojho začiatočného políčka na ľubovoľné zo 4 políčok, ktoré so začiatočným susedia stranou (políčka so súradnicami \((0,1)\), \((1,0)\), \((0,-1)\) a \((-1,0)\))? Prečo to nejde na menej skokov?

4. (2 body) Jazdec zo svojho začiatočného políčka urobil presne tri skoky. Na koľkých rôznych políčkach môže teraz stáť? Popíšte postup, ktorým ste sa dopracovali k svojmu riešeniu. Na rozdiel od podúlohy b) nemusíte do popisu písať súradnice týchto políčok.

5. (3 body) Koľko najmenej skokov potrebuje jazdec na cestu z políčka \((0,0)\) na políčko \((9,9)\)? Prečo to nejde na menej? Popíšte postup, ktorým ste sa dopracovali k svojmu riešeniu.

6. (4 body) Popíšte všeobecný postup, ako by ste zisťovali, na koľko najmenej skokov sa vie jazdec dostať z políčka \((0,0)\) na políčko \((X,Y)\). Skúste popísať, prečo je váš postup správny.

---

1. Políčko \((0,0)\) je v strede Emovej obývačky a šachovnica je nekonečná do všetkých smerov. Áno, Emova obývačka je naozaj veľká :)↩

1. (2 body) Políčko \((0,0)\) má bielu farbu a zvyšené políčka sú ofarbené šachovnicovo. Akú farbu bude mať políčko, na ktoré sa jazdec dostane po \(X\) skokoch? Prečo?

Všimnite si, že kôň pri každom skoku zmení farbu, na ktorej stojí. Túto vlastnosť je dobre vidieť na obrázku zo zadania, ktorý ukazuje všetky platné skoky koňa.

Kôň začal na bielom políčku a všetky jeho skoky vedú na čierne políčko. Analogicky ak kôň skočí z čierneho políčka, skončí na bielom políčku. Po dvoch skokoch teda vždy bude na farbe, na ktorej začínal. Preto ak je \(X\) párne, kôň skončí na bielom políčku, a naopak, ak je \(X\) nepárne, skončí na čiernom.

2. (2 body) Jazdec zo svojho začiatočného políčka urobil presne dva skoky. Na koľkých rôznych políčkach môže teraz stáť? Aké súradnice majú tieto políčka?

Vieme, kam sa jazdcom dá dostať na jeden skok (obrázok vyššie). Skúsime teda z každej z týchto pozícií skočiť s jazdcom znovu.

Na obrázku zelené jednotky značia, kam sa vieme dostať na jeden skok a červené súradnice sú práve súradnice pozícií, kam sa možno dostať na dva skoky. Všimnite si, že ak políčko \((0,0)\) posadíme do stredu súradnicovej sústavy, možné pozície kam sa vieme dostať na dva skoky, budú symetrické podľa osí pretínajúcich \((0,0)\) zvisle aj vodorovne. Stačí preto nájsť políčka v jednom z kvadrantov, napríklad prvom, ktorý je na obrázku označený bledomodrým pozadím. V rovine je kvadrant jeden zo štyroch výsekov určenými osami súradníc. Číslujeme ich \(I-IV\) tak, ako na obrázku nižšie.

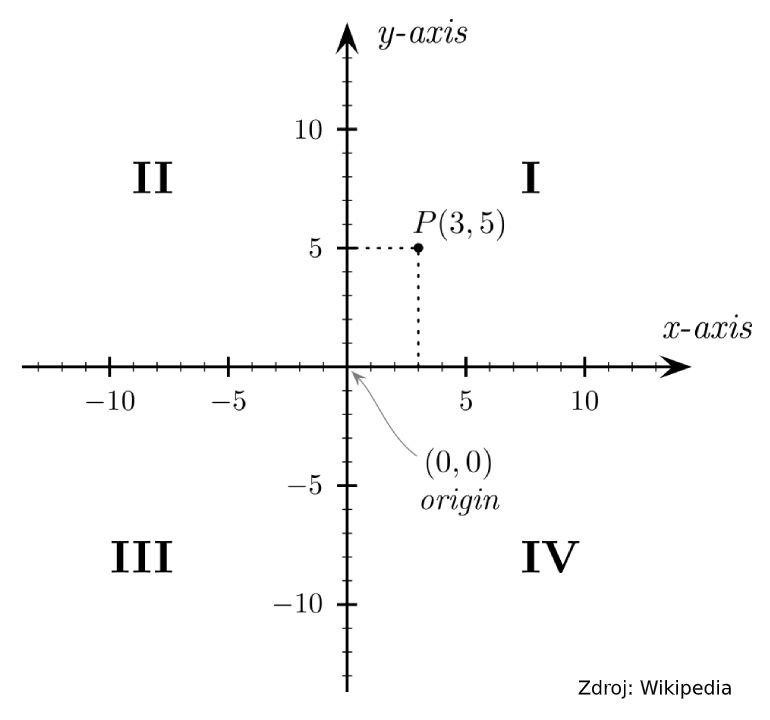
Políčka z prvého kvadrantu zobrazíme do ostatných podľa osových súmerností jednoducho – zmeníme im znamienka pri súradniciach. Napríklad políčku \((3,1)\) v ostatných kvadrantoch zodpovedajú súradnice \((-3,1)\), \((-3,-1)\), \((3,-1)\). Vďaka tomu všetky políčka, na ktoré sa vieme dostať na dva skoky, môžeme zapísať stručnejšie: \[\{(xi, yi) \mid (x,y) \in \{(0,0), (2,0), (4,0), (1,1), (3,1), (0, 2), (4,2), (1,3), (3,3), (0,4), (2,4)\}, i,j \in \{-1,1\}\}\] Vytvorili sme množinu, ktorá obsahuje všetky dvojice \((x,y)\) z prvého kvadrantu a ich obrazy v ostatných kvadrantoch \((-x,y)\), \((-x,-y)\), \((x,-y)\).

3. (2 body) Koľko najmenej skokov potrebuje jazdec na to, aby sa dostal zo svojho začiatočného políčka na ľubovoľné zo 4 políčok, ktoré so začiatočným susedia stranou (políčka so súradnicami \((0,1)\), \((1,0)\), \((0,-1)\) a \((-1,0)\))? Prečo to nejde na menej skokov?

Všimnite si, že na pozíciu \((1,0)\) sa vieme dostať napríklad z políčka \((3,1)\), kam sme sa dostali na 2 skoky (viď. predchádzajúca podúloha). Na políčko \((1,0)\) sa vieme teda dostať na najviac 3 skoky. Obdobne sa vďaka symetrii na najviac 3 skoky vieme dostať aj na políčka \((0,1)\), \((0,-1)\) a \((-1,0)\).

Prečo to nejde na menej skokov ako 3? Našli sme všetky políčka, ktoré vieme navštíviť na 0 skokov (\((0,0)\)), 1 skok (obrázok z \(a)\)), 2 skoky (obrázok z \(b)\)) a v žiadnych z nich sa políčka susedné s \((0,0)\) nenachádzali. Na tieto pozície sa vieme dostať na jeden skok až vďaka políčkam, ktoré sme objavili na 2 skoky. Spolu sú to tak 3 skoky.

4. (2 body) Jazdec zo svojho začiatočného políčka urobil presne tri skoky. Na koľkých rôznych políčkach môže teraz stáť? Popíšte postup, ktorým ste sa dopracovali k svojmu riešeniu. Na rozdiel od podúlohy b) nemusíte do popisu písať súradnice týchto políčok.

Podobne ako v podúlohe b) využijeme symetriu. Nájdeme všetky políčka v prvom kvadrante, kam sa vieme dostať na jeden skok, potom na dva, až na koniec na tri.

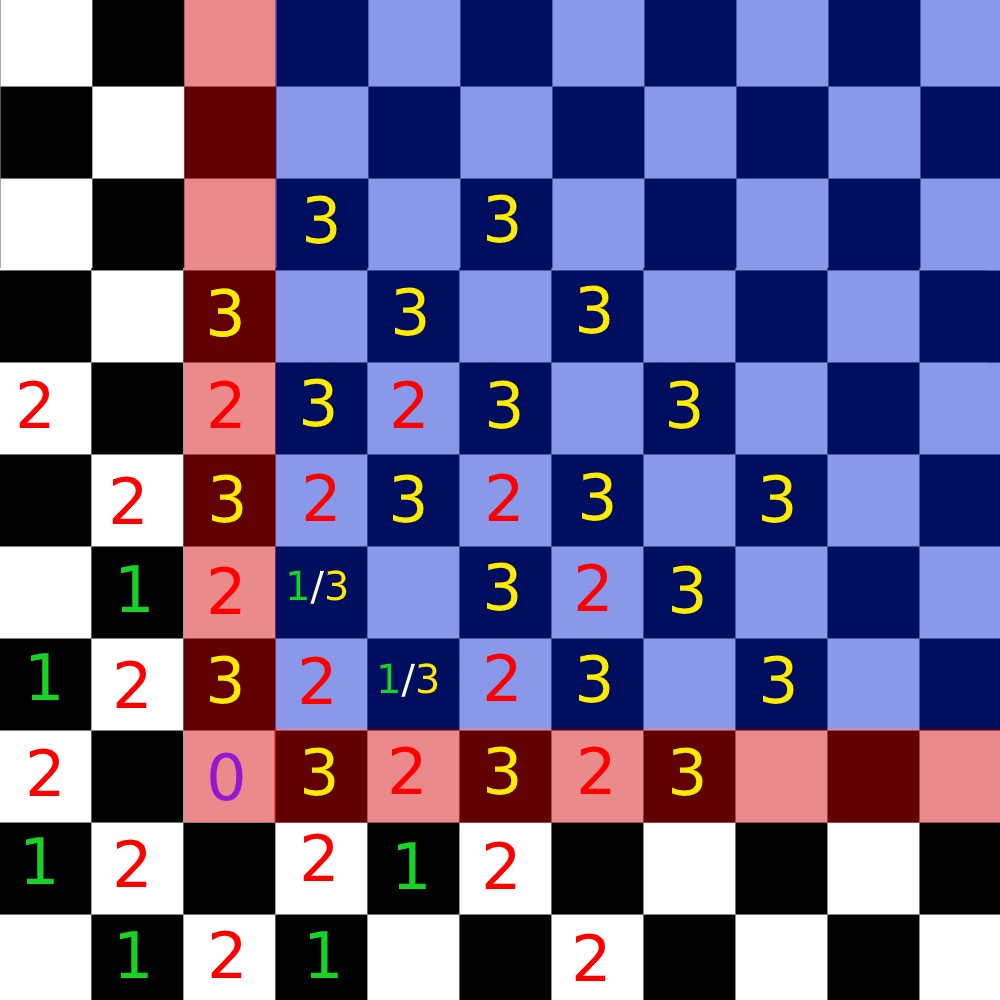
Z obrázku vidíme, že v jednom kvadrante je \(22\) políčok, ktoré vieme navštíviť práve na tri skoky. Nestačí ale \(22\) vynásobiť štyrmi za každý kvadrant, pretože políčka na osiach by sme započítali dvakrát. Rozdelíme si preto počty políčok na tie v strede \(S = 16\) a tie na osiach \(O = 6\). Na obrázku sú stredné políčka označené modrou a obvodové červenou farbou. Teraz stačí stredy započítať štyrikrát za každý kvadrant a osi iba dvakrát: \[4 \cdot S + 2 \cdot O = 4 \cdot 16 + 2 \cdot 6 = 76\].

5. (3 body) Koľko najmenej skokov potrebuje jazdec na cestu z políčka \((0,0)\) na políčko \((9,9)\)? Prečo to nejde na menej? Popíšte postup, ktorým ste sa dopracovali k svojmu riešeniu.

Skúsime postupne nachádzať políčka, na ktoré sa vieme dostať najskôr na \(1, 2, 3, \ldots\) skoky. Predstavte si, že postupne z bodu \((0,0)\) odhaľujeme šachovnicu a na každé políčko, na ktoré skočíme, si zapíšeme, v ktorom skoku sa nám tam podarilo prvýkrát dostať.

Do bodu \((0,0)\) sa vieme dostať na \(0\) skokov. Z neho vieme postupne skočiť na osem políčok, ktoré sme predtým ešte nenavštívili. Tieto políčka označíme za Vlnu 1, pretože sú to políčka, na ktoré sa vieme dostať najskôr na \(1\) skok. Zapíšeme si preto na ich pozície \(1\) a skúsime z týchto \(8\) políčok postupne skočiť ďalej. To nám spolu dá \(8 \cdot 8\) nových pozícií. Niektoré políčka možno navštívime dvakrát. Napríklad určite pri tomto kroku skočíme späť do počiatku \((0,0)\). Tu však počet skokov už nevylepšíme, pretože sme sa sem aktuálne dostali na \(2\) skoky, pričom pri \((0,0)\) sme si predtým poznačili, že sa tam vieme dostať na \(0\) skokov. Z bodu \((0,0)\) sa nám už preto neoplatí skákať ďalej, pretože by sme objavovali už objavené políčka a navyše s väčším počtom skokov!

Avšak na pozície, ktoré sme navštívili prvýkrát, si zapíšeme počet skokov \(2\) a označíme ich za Vlnu 2. Z Vlny 2 potom skúsime skákať ďalej a vytvoríme Vlnu 3, z Vlny 3 skáčeme ďalej a vytvoríme Vlnu 4, atď. Na obrázku môžete vidieť tento postup v prvom kvadrante, až pokiaľ nedosiahneme bod \((9,9)\) vpravo hore, označený bledomodrou farbou. Z obrázku vidíme, že na toto políčko sme sa prvýkrát dostali po \(6\) skokoch. Prečo to nejde na menej? Vlna i totiž obsahuje práve tie políčka, na ktoré sa vieme dostať najskôr na \(i\) skokov.

Alternatívne sa táto podúloha dala vyriešiť trochu jednoduchšie, s použitím symetrie stačilo spraviť prvé \(3\) kroky “vlny” (skúste sa zamyslieť prečo):

6. (4 body) Popíšte všeobecný postup, ako by ste zisťovali, na koľko najmenej skokov sa vie jazdec dostať z políčka \((0,0)\) na políčko \((X,Y)\). Skúste popísať, prečo je váš postup správny.

Vlna \(i\) z predošlej podúlohy obsahuje práve tie políčka, do ktorých sa vieme dostať najskôr na \(i\) skokov. Prečo? Ak sa na ľubovoľné, doteraz nenavštívené, políčko \(P\) vieme dostať z nejakého políčka z Vlny i-1, potom najkratšia cesta skokmi do políčka \(P\) musí mať dĺžku \(i\), pretože \(P\) nebolo objavené v skorších vlnách. Zároveň do Vlny i pridáme všetky doteraz neobjavené políčka, na ktoré vieme skočiť z políčok Vlny i-1. Vlna i tak obsahuje všetky políčka, do ktorých sa vieme dostať najskôr na \(i\) skokov. Na záver, Vlna 0 triviálne obsahuje všetky vrcholy s najkratšou cestou dĺžky 0, pretože obsahuje jediné políčko \((0,0)\).

Na nájdenie najmenšieho počtu skokov potrebných na dosiahnutie bodu \((X,Y)\) tak stačí pokračovať s “Algoritmom vlny” popísaným vyššie až dovtedy, pokiaľ nenarazíme na bod \((X,Y)\). Ak naň narazíme v \(i\)-tej vlne, vieme, že najkratšia cesta do \((X,Y)\) je dlhá \(i\) skokov.

“Algoritmus vlny” popísaný vyššie sa volá BFS (Breadth first search) alebo po slovensky Hľadanie do šírky. Všimnite si, že názov odpovedá presne tomu, čo algoritmus vykonáva. Postupne zo všetkých políčok v aktuálnej vlne skúsime objaviť ďalšie, čím objavujeme mapu do všetkých smerov, teda do šírky. Ide o takzvaný grafový problém (jednotlivé políčka tvoria vrcholy grafu). Ak sa chceš dozvedieť viac o grafoch v informatike a o tom ako sa prehľadávanie do šírky implementuje pomocou fronty, pozri sa do našej kuchárky alebo do knihy Průvodce labyrintem algoritmů.