Zadanie
Ak nevieš programovať, nezúfaj! Môžeš sa to naučiť a ešte za to získať body, ktoré sa ti budú počítať namiesto tejto úlohy.
Stačí, že pôjdeš na stránku Programátorskej Liahne (liahen.ksp.sk). Keď budeš riešiť sadu arrays_cpp, bodmi, ktoré získaš si môžeš nahradiť riešenie tejto úlohy. Stačí ak na spodku tejto stránky odovzdáš pdf-ko s prezývkou, ktorú používaš na Liahni.
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Romanovi na [email protected]
V Absurdistane už od nepamäti funguje inštitúcia OIA (Ochrana Integrity Absurdistanu). V poslednej dobe sa ale na ňu valí veľká vlna kritiky. Špión Paroháč pri poslednej misii v Blahostane špiónoval tak dobre, že sa mu podarilo preniknúť do radov miestnej inštitúcie OIB (Ochrana Integrity Blahostanu). Tí mu ponúkli lukratívne miesto, ktorému Paroháč neodolal a prezliekol kabát. Pre Absurdistan teraz Paroháč predstavuje hrozbu.
Zatiaľ o Paroháčovom prešľape vie iba Hlaváč, šéf OIA. Na zatknutí Paroháča už aktívne pracuje. Zatiaľ vytvoril sieť zo svojich špiónov, v ktorej každý špión sleduje práve jedného iného špióna. Navyše, pretože Hlaváč neverí nikomu, platí, že každý špión je sledovaný práve jedným iným špiónom.
Hlaváč plánuje vyslať všetkých špiónov do Blahostanu. Potrebuje z nich vybrať čo najviac takých, ktorým o Paroháčovom prešľape povie. Nemôže však vybrať všetkých – aby dokonale fungovala jeho stratégia vzájomnej kontroly, musí každý zo špiónov, ktorý o prešľape vie, byť sledovaný špiónom, ktorý o prešľape nevie. Hlaváčovi by teraz veľmi pomohlo, keby ste zistili, koľko takýchto špiónov môže vybrať.
Úloha
Na vstupe dostane sieť špiónov, o ktorej platí, že každý špión sleduje práve jedného iného špióna a práve jedným špiónom je aj on sám sledovaný. Vašou úlohou je nájsť maximálny počet špiónov, ktorým môže Hlaváč vyzdradiť tajomstvo o Paroháčovi tak, aby platilo, že každý z týchto špiónov je sledovaný špiónom, ktorý o tajomstve nevie.
Formát vstupu
Na prvom riadku vstupu je jedno kladné číslo \(n\) (\(2 \leq n \leq 10^{6}\)), počet špiónov. Tých si očíslujeme od 1 po \(n\). Na druhom riadku vstupu je \(n\) medzerou oddelených čísel, pričom \(i\)-te číslo je číslo špióna, ktorý je sledovaný \(i\)-tym špiónom.
Formát výstupu
Na výstup vypíšte jediné číslo – maximálny počet špiónov, ktorým vie Hlaváč vyzdradiť svoje tajomstvo.
Hodnotenie
| Číslo sady | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| maximálne \(n\) | \(10\) | \(20\) | \(1000\) | \(200\,000\) | \(1\,000\,000\) |
Príklady
Input:
5
5 3 2 1 4Output:
2Hlaváč môže svoje tajomstvo povedať napríklad špiónom 3 a 4. Špión 3 je sledovaný špiónom 2 a špión 4 špionom 5, pričom 2 ani 5 o tajomstve nevedia. Uvedomte si, že viac špiónov vybrať nemôžeme, pretože inak by nutne aspoň jeden z nich bol sledovaný iným z vybraných špiónov. Odpoveď je preto 2.
Na vstupe dostaneme sieť špiónov, o ktorej platí:
- Každý špión sleduje práve jedného iného špióna.
- Každý špión je sledovaný práve jedným iným špiónom.
Našou úlohou je zistiť koľko najviac špiónov môžeme vybrať tak, aby boli sledovaní nevybranými špiónmi.
Špióni na grafe
Úlohu si môžeme vizualizovať pomocou grafu. Grafom myslíme “informatický” graf, nie matematický. Informatický graf obsahuje vrcholy (bodky) a hrany (čiary medzi vrcholmi).
Špióni budú vrcholy a vzťah “špión \(A\) sleduje špióna \(B\)” zakreslíme pomocou hrany z \(A\) do \(B\). Napríklad:
5
5 3 2 1 4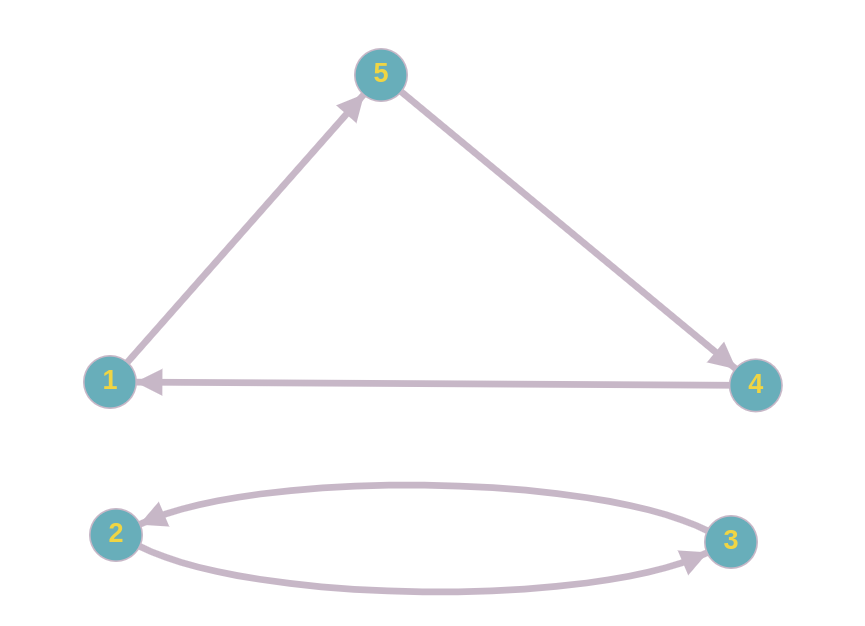
Hrany na našom grafe majú na jednej strane šípku. Takýmto hranám hovoríme orientované. Hrana vždy smeruje k sledovanému špiónovi.
Špióni tvoria cykly
Všimnite si, že vďaka podmienkam 1) a 2) vyššie platí, že do každého vrcholu vstupuje práve jedna hrana (hlavička šípky) a práve jedna hrana vystupuje (päta šípky). To znamená, že ak budeme od nejakého vrcholu \(A\) postupovať ďalej po hranách, vždy skončíme späť vo vrchole \(A\). Cestu, ktorá začne a skončí v rovnakom vrchole nazývame cyklus. V okrajovom prípade použije takáto cesta všetkých \(n\) hrán, viď. nasledujúci príklad.
6
2 6 4 5 1 3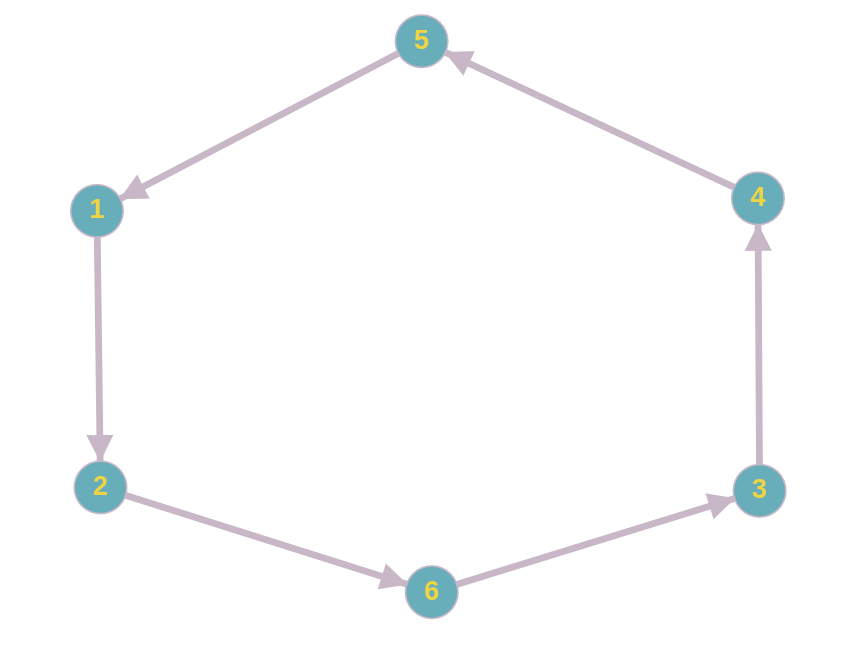
Koľko najviac špiónov môžeme v tomto príklade vybrať tak, aby boli sledovaní nevybranými špiónmi? Alebo inak, koľko najviac vrcholov môžeme vybrať tak, aby do nich nevstupovala hrana z už vybraného vrcholu? Odpoveď je 3. Na začiatku vyberieme ľubovoľného špióna a ďalej vyberáme každého druhého až pokiaľ neprejdeme celý cyklus. Pre cyklus párnej dĺžky \(d\) je tak odpoveď \(d / 2\). Podobne sa dá ukázať, že pre cyklus nepárne dĺžky je odpoveď \(d / 2\) zaokrúhlené nadol.
Takto dostávame myšlienku algoritmu: rozložíme graf na cykly a už vieme, že z každého cyklu môžeme vybrať polovicu vrcholov.
Riešenie rekurziou
Nasledujúce riešenie nájde cykly rekurzívne.
Každý cyklus objavíme práve raz, pretože pri objavovaní označíme všetky vrcholy cyklu za navštívené. Okrem toho iba v jednom cykle prejdeme všetky vrcholy. Časová zložitosť je tak \(O(n)\). Pamäťová zložitosť je rovnako \(O(n)\), pretože používame iba dve polia na načítanie vstupu obsahujúce \(n\) čísel.
Časová zložitosť je zjavne optimálna (lepšie riešenie ako \(O(n)\) nevymyslíme, pretože potrebujeme načítať vstup). Zároveň ale tento program stačí iba na 9 bodov. Dôvodom je rekurzia, ktorá sa pri najväčšom vstupe môže zanoriť až \(1\,000\,000\)-krát. Pretože hlboká rekurzia je pamäťovo náročná, program na testovači spadne na pretečenie pamäte a dostaneme hlášku “Chyba počas behu programu”.
Riešenie bez rekurzie
Toto riešenie využíva rovnakú myšlienku ako to predošlé, ale rekurziu sme nahradili cyklom. To stačí na 15 bodov :)
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.