2. Reprezentácia telefónnych čísel vzorové riešenie

Zadanie

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Žabovi na [email protected]

Adam sa minulú nedeľu, ako vzorný vnuk, rozhodol zavolať svojej babke. Jej telefónne číslo si pamätá odmala, začal ho preto vyťukávať do mobilu. V polovici písania však Adamova obrazovka vyzerala zhruba takto a kontakt na babku bol automaticky doplnený.

Adam sa zháčil. Takúto funkcionalitu pokladal za samozrejmú, nikdy sa však nezamyslel, ako to vlastne ten mobil robí. Podľa čoho si vie tipnúť zadávané číslo a dokonca povedať koľko ďalších možností ešte existuje? Zrazu zabudol na to čo robil a začal sa vŕtať v pamäti telefónnu. Pomôžte Adamovi odpovedať na jeho otázky, nech stihne zavolať babke.

Úloha

1. (1 body) Adam si do mobilu stiahol program, ktorý mu umožňuje prezerať si vnútornú pamäť telefónnu. Hneď ho aj spustil s tým, že mu má zobraziť pamäť patriacu kontaktom. Program preňho vygeneroval nasledovný obrázok.

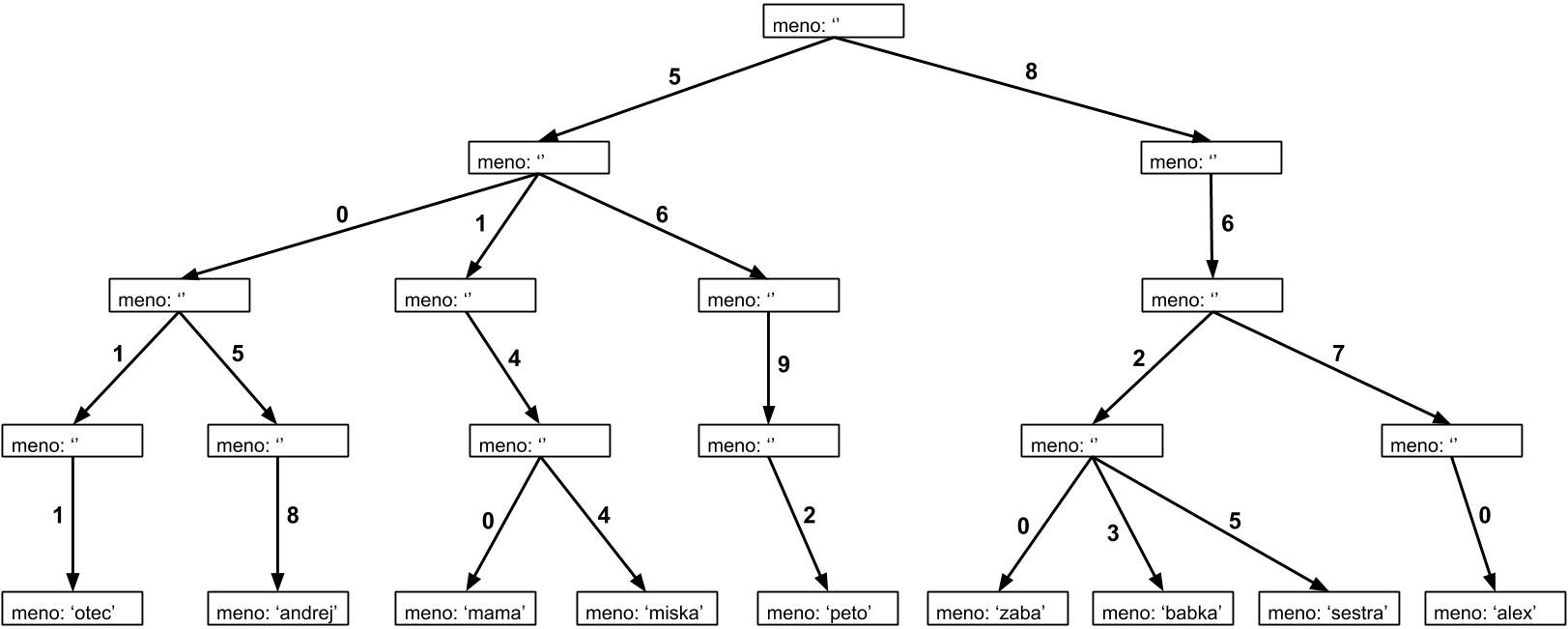
Adam však vôbec nerozumie tomu, čo má táto reprezentácia znamenať. A jediný kontakt, ktorý si pamätá je na jeho babku, ktorá má číslo 8623 (nečudujte sa, štvormiestne čísla sú tam kde žije Adam úplne bežné).

Z uvedeného obrázku vydedukujte, aké všetky kontakty má Adam uložené v telefónne. Pre každý kontakt určite aj telefónne číslo, ktoré mu prislúcha.

2. (2 body) Ako by vyzeral obrázok vygenerovaný stiahnutým programom, ak by mal Adam uložené nasledovné kontakty:

    mama:   091576          ujo:    091497          brat:  091256           janka: 092730
    sestra: 092576          stryko: 091483          lucka: 092578           sysel: 093037
    babka:  091547          peter:  092530          jonas: 092098           radka: 091418

3. (4 body) Adama by zaujímalo, ako vie jeho mobil pomocou uvedenej reprezentácie dopĺňať kontakt, ku ktorému by dané číslo mohlo patriť. Vašou úlohou je vymyslieť postup, ktorý po zadaní niekoľkých prvých cifier čísla nájde ľubovoľný kontakt, ktorého číslo začína na zadané cifry. Poprípade oznámi, že žiadny taký kontakt sa v mobile nenachádza.

   Napríklad, ak by sme sa pozreli na kontakty z podúlohy b), tak po napísaní 0914 by Adamov mobil mohol navrhnúť kontakt radka ale takisto kontakty ujo alebo stryko. A v prípade, že by Adam napísal iba 0, mohol by mu mobil ponúknuť ľubovoľný z jeho kontaktov. Ak by sa však pomýlil a napísal by 08 ako začiatok čísla, mobil by mu povedal, že žiaden vhodý kontakt neexistuje.

   Vaše riešenie by malo fungovať pre každú možnú množinu kontaktov. Jednak sa teda môže meniť počet kontaktov a takisto dĺžka jedného čísla. Môžete však predpokladať, že všetky čísla majú rovnakú dĺžku a že tieto kontakty sú v pamäti reprezentované rovnako ako v podúlohách a) a b).

   Taktiež sa snažte, aby bolo vaše riešenie čo najefektívnejšie, teda potrebovalo spraviť čo najmenej úkonov. Napríklad ak by sme mali \(10\,000\) desaťmiestnych telefónnych čísel zapísaných vo vyššie uvedenej štruktúre, optimálne riešenie by sa stále dalo simulovať aj ručne.

4. (5 body) Keď Adam do pamäte zapísal dlhšie čísla, hral sa aj s 1000 cifernými číslami, zdalo sa mu, že mu mobil začal sekať. Niekde v nastaveniach však našiel tlačidlo “Zoptimalizuj kontakty”, ktoré po stlačení citeľne urýchlilo dopĺňanie kontaktov. Keď sa opäť pozrel do pamäte telefónnu, s prekvapením zistil, že jej reprezentácia sa zmenila.

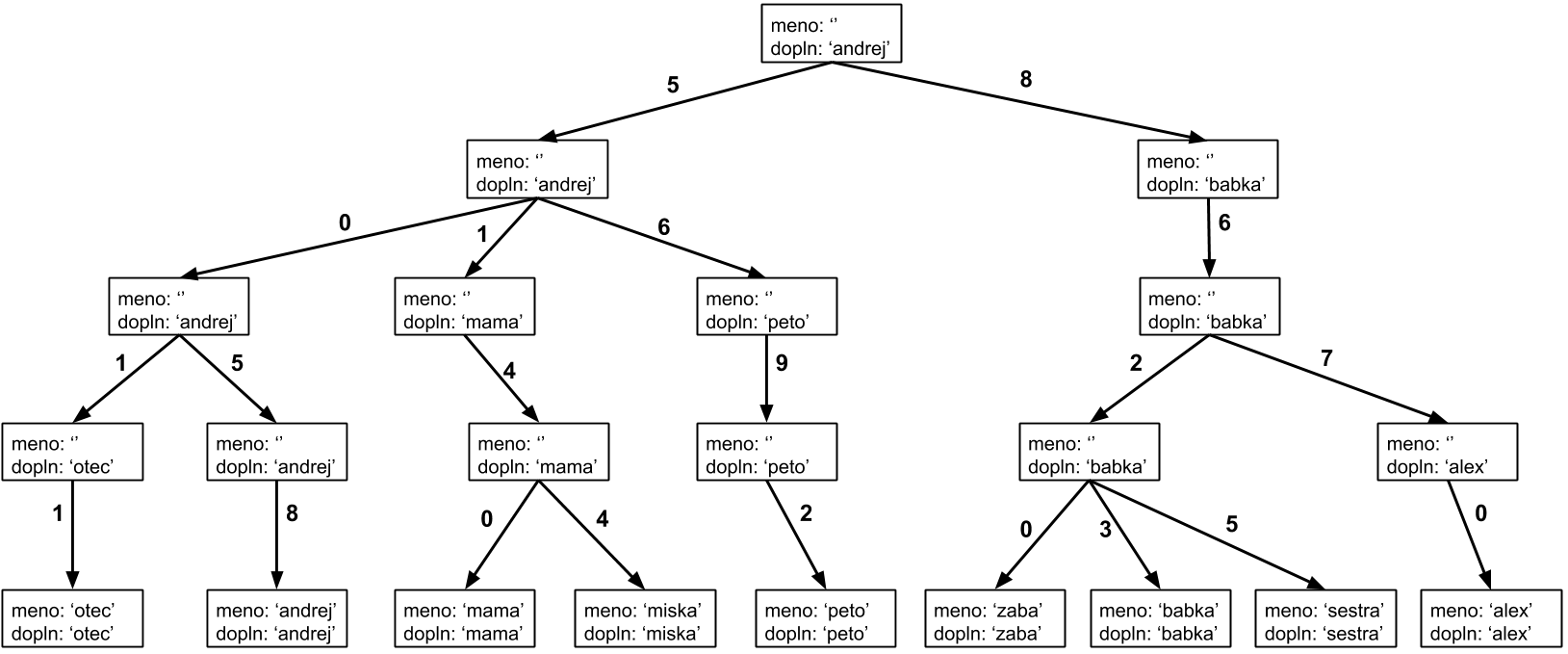
Upravte váš postup z podúlohy c) tak, aby využíval nové údaje z pamäte. Prečo je toto riešenie rýchlejšie ako to predošlé? Okrem toho vymyslite postup, ktorým boli hodnoty dopln vypočítané. Máte teda popísať postup, ktorý sa vykoná keď je stlačené tlačidlo “Zoptimalizuj kontakty”, a ktorý doplní do pamäte nové hodnoty. Tento postup by mal fungovať na ľubovoľnej množine kontaktov.

5. (3 body) S počítaním možností je však stále problém. Síce to Adamov mobil robí správne, trvá mu to príliš dlho. A žiadne tlačidlo “Zoptimalizuj počet” neexistuje. Rozhodol sa preto, že si ho do mobilu doprogramuje, nevie však, ako má toto tlačidlo pracovať. Vymyslite a podrobne popíšte čo sa má stať po stlačení tlačidla “Zoptimalizuj počet”. Následne popíšte, ako bude telefón pre zadaný začiatok čísla zisťovať počet čísel s rovnakým začiatkom.

Podúloha a.

Zistiť, ktoré kontakty sú v telefónne nie je ťažké, stačí prečítať všetky mená v spodnom riadku obrázku. Ak k nim však chceme priradiť čísla, musíme si uvedomiť, ako táto reprezentácia funguje. Pomôcť nám pri tom môže kontakt babka so známym číslo 8623.

Keď tieto čísla hľadáme na obrázku, ľahko si všimneme, že zodpovedajú šipkám, ktoré vedú z vrchu až ku kontaktu s menom babka. Je preto prirodzené, že rovnaká vlastnosť bude platiť aj pre zvyšné kontakty. Ak teda chceme zistiť telefónne číslo pre zadaný kontakt, prejdeme po šipkách od vrchu obrázku k jeho spodku. Dostávame nasledovné kontakty:

otec:   5011        miska:  5144        babka:  8623
andrej: 5058        peto:   5692        sestra: 8625
mama:   5140        zaba:   8620        alex:   8670

Podúloha b.

Našou úlohou je nakresliť obrázok zo zadaných kontaktov. V predchádzajúcej podúlohe sme si všimli, že šipky od vrchu obrázku ku konkrétnemu kontaktu majú označenie podľa jednotlivých cifier príslušného čísla. Pri kreslení je však dôležitá ešte jedna vlastnosť, ktorú si ľahko všimneme. Z každého obdĺžnika vychádza najviac jedna šipka s konkrétnou cifrou. Vďaka tomu spájame dokopy čísla s rovnakým začiatkom a rozdeľujeme ich až keď je to naozaj nevyhnutné.

Na obrázku zo zadania napríklad vidíme, že z vrchného obdĺžnika nevychádza 8 šipiek, jedna pre každý kontakt, ale iba 2, pretože všetky kontakty v Adamovom telefónne začínajú číslom 5 alebo 8. Keď sa pozrieme do zadaných kontaktov, všimneme si, že všetky začínajú na 09. To znamená, že z najvrchnejších dvoch obdĺžnikov bude vychádzať iba jedna šipka a až na tretej úrovni sa to začne rozdeľovať.

Podúloha c.

Skôr ako sa pustíme do riešenia úlohy, zaveďme si nejaké označenie, aby sa nám o ňom ľahšie rozprávalo. Celý náš obrázok vyzerá ako strom (obrátený hore nohami), budeme preň preto používať toto označenie. Jednotlivé obdĺžniky nazveme vrcholy a šipky z nich hrany. Najvrchnejší vrchol má naviac špeciálny význam a preto aj názov – koreň.

Pre zadaný začiatok čísla máme nájsť ľubovoľný kontakt, ktorého telefónne číslo má rovnaký začiatok. Kde by sa však mohol nachádzať? Ako sme si všimli už v podúlohe b., všetky kontakty s rovnakým začiatkom sa v našom strome nachádzajú pokope. Naviac, ich umiestnenie vieme ľahko nájsť, stačí ísť od koreňa stromu po hranách s príslušnými ciframi.

Zoberme teda zadaný začiatok čísla. Začnúc v koreni stromu sa postupne posúvame po hranách, ktorých označenie zodpovedá ďalšej cifre tohto čísla. Uvedomme si, že v každom momente sa pod aktuálnym vrcholom nachádza časť stromu (podstrom), v ktorom sú všetky kontakty začínajúce sa na už spracovaný úsek čísla. Keď teda spracujeme celé zadané číslo, budeme vo vrchole, pod ktorým sú všetky kontakty, ktoré majú takýto začiatok telefónneho čísla. My si môžeme vybrať ľubovoľný z nich. To znamená, že odtiaľto je už jedno po ktorých hranách prejdeme, stačí že pôjdeme dodola až kým sa nedostaneme k vrcholu, ktorý obsahuje meno niektorého kontaktu a toto meno vypíšeme.

Uvedomme si ešte, že sa mohlo stať, že žiadny kontakt nezačínal na zadané číslo. To znamená, že v niektorom momente našeho postupu sme chceli použiť nejak označenú hranu, ktorá ale z aktuálneho vrcholu nevychádzala. V tom momente sme teda mohli postup ukončiť a vyhlásiť, že taký kontakt v mobile nie je.

Nami navrhnutý postup je navyše pomerne efektívny. V každom jeho kroku sa totiž posunieme o jednu úroveň nižšie, spracujeme jednu cifru telefónneho čísla. Bez ohľadu na to, koľko kontaktov má Adam v telefónne bude počet krokov tohto algoritmu úmerný dĺžke telefónnych čísel.

Podúloha d.

Po stlačení tlačidla “Zoptimalizuj kontakty” sa nám do každého vrchola pridala položka dopln. Z obrázku ľahko vydedukujeme, že táto hodnota zodpovedá jednému menu kontaktu, ktoré sa nachádza v podstrome príslušného vrcholu.

Riešenie z prechádzajúcej podúlohy bude teraz zrazu oveľa jednoduchšie. Tak ako predtým pôjdeme z koreňa stromu po hranách označených príslušnými ciframi. Keď však spracujeme celé zadané číslo, nemusíme v našom zostupe pokračovať. Jednoducho sa pozrieme na hodnotu dopln vo vrchole, kde sme zastavili a použijeme tú. Presne to totiž táto hodnota predstavuje – ľubovoľný kontakt začínajúci správnym číslom.

O niečo komplikovanejšie je vymyslieť, ako tieto hodnoty spočítať. Prvé riešenie, ktoré nám môže napadnúť je pomerne priamočiare. Pre každý vrchol pôjdeme dodola po ľubovoľných hranách až kým sa nedostaneme k nejakému kontaktu a tento kontakt do tohto vrcholu zapíšeme. To je však strašne pomalé, pre každý vrchol totiž musíme spraviť zhruba toľko operácií, ako dlhé sú čísla.

Ako to teda vyriešiť jednoduchšie? Možno neriešme všetko naraz, ale pozrime sa na tie vrcholy, pre ktoré je odpoveď triviálna. To sú všetky tie v najnižšej úrovni nášho stromu. Pre každý vrchol, ktorý má priradené meno totiž môžeme rovno doplniť aj rovnakú hodnotu dopln. V tomto podstrome je totiž iba jeden vyhovujúci kontakt a to práve tento.

No a keď už máme najspodnejšie vrcholy spracované, ktoré ďalšie vieme doplniť veľmi jednoducho? Predsa tie nad nimi! Každý z vrcholov nad nimi si vyberie jedného svojho syna (vrchol priamo pod ním) a použije jeho hodnotu dopln, je pritom jedno, ktorého syna si vyberie. Vďaka tomu ale vieme rýchlo vyriešiť aj tretiu vrstvu odspodu. Všetci synovia vrcholu na tejto vrstve už majú doplnenú hodnotu dopln. Opäť mu teda stačí si vybrať ľubovoľného syna a hodnotu dopln skopírovať.

Všimnite si ten výrazný rozdiel týchto dvoch riešení. V prvom sme začínali z vrchu a zakaždým sme museli ísť až po spodok, aby sme sa dostali k relevantnej informácii. V druhom riešení však začíname už známymi informáciami a postupne ich posúvame dohora. Pre každý vrchol nám teda stačí pozrieť sa na jedného z jeho synov a iba z neho skopírovať dopln, čo je rýchlejšie, ako keď sme museli ísť úplne dodola. Pre každý vrchol spravíme len jedinú operáciu.

Podúloha e.

Keď rozumieme riešeniu podúlohy d., vyriešiť podúlohu e. je jednoduché. Použijeme rovnaký prístup. Do každého vrcholu si pridáme novú hodnotu pocet. Táto hodnota označuje počet kontaktov v podstrome určenom daným vrcholom. Táto hodnota je jasne určená pre spodnú vrstvu vrcholov, kde platí, že pocet: 1.

No a počet kontaktov v podstrome nejakého vyššieho vrchola vieme vypočítať cez súčet počtov kontaktov v jeho synoch. Opäť teda budeme postupovať od spodku stromu a postupne upravovať informáciu v jednotlivých vrcholoch. Pre každý vrchol budeme musieť spočítať hodnoty pocet všetkých vrcholov priamo pod ním. Vďaka tomu zistíme, koľko kontaktov začína na zadané číslo.

Postup vypisovania tohto čísla je už potom rovnaký ako v podúlohe d., jednoducho prejdeme po hranách, ktoré zodpovedajú číslam zadaným používateľom a vypíšeme hodnotu pocet z posledného takto navštíveného vrcholu.

Písmenkový strom

Štruktúra, ktorú sme si predstavili v tejto úlohe sa volá písmenkový strom (po anglicky tiež trie) a väčšinou sa používa na ukladanie slov, ktoré sú tým pádom tiež zoskupené podľa ich začiatkov.

S pomocou písmenkových stromov vieme počítať množstvo zaujímavých informácií o uložených slovách alebo číslach a aj keď reálne použitie je častokrát komplikovanejšie, základná myšlienka ostáva rovnaká. Pri hľadaní postupuj od vrchu po zodpovedajúcich hranách a pri predpočítavaní posúvaj informáciu od spodu stromu ku koreňu.