Zadanie
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Dávidovi na [email protected]
Táto úloha voľne nadväzuje na úlohu Pohodlné kreslo z prechádzajúceho kola. Odporúčame si preto aspoň letmo prečítať jej zadanie aj vzorové riešenie. Na vyriešenie tejto úlohy to síce nie je nutné, myslíme si však, že vám to vie pomôcť.
Tomi už vďaka vám zistil, aký úžasný a krásny je jeho programovací jazyk Kreslo. Niečo mu v ňom však stále chýbalo. Nech sa snažil ako chcel, nedarilo sa mu v ňom nakresliť program, ktorý by zoradil čísla od najmenšieho po najväčšie. Uvedomil si, že na vyriešenie totho problému potrebuje viac ako 26 registrov, začal si ich preto číslovať. Aby nemusel meniť už existujúce príkazy Kresla, rozhodol sa, že hodnota v registri D bude závisieť od hodnoty v registri A (adresa). To znamená, že pre každú hodnotu v registri A predstavuje D úplne iný register. Túto zmenu pochopíte najlepšie na praktickej ukážke, ktorú sme pre vás pripravili: https://ksp.sk/~prask/specialne/4/2/3/index.html?ukazka=4.
Úloha
Kreslo je veľmi jednoduchý jazyk. Pracuje iba s celými číslami, ktoré vie načítavať zo vstupu a vypisovať na výstup. Aby sa Tomimu ľahko kreslilo, celý program je nakreslený do mriežky a každá inštrukcia zaberá jeden štvorec. Podrobnosti o tom, ako tento jazyk funguje a ako v ňom písať programy nájdete na ksp.sk/~prask/specialne/4/2/3/manual.pdf.
Našťastie, my môžeme používať elektronický editor, ktorý dokáže simulovať beh programu. Nájdete ho spolu s ukážkovými programami na ksp.sk/~prask/specialne/4/2/3/.
Vašou úlohou bude vyriešiť nasledujúce podúlohy a odovzdať ZIP súbor, ktorý obsahuje zdrojové kódy vašich riešení (dajú sa stiahnuť z editora). ZIP by mal obsahovať súbory 1.kr až 5.kr s vašimi riešeniami jednotlivých podúloh.
Podúlohy
- (2 bod) Na vstupe je číslo \(n\) a potom dva krát \(n\) čísel. Na výstup vypíšte najskôr druhých \(n\) čísel a po nich prvých \(n\) čísel.
Input:
3 1 2 3 4 5 6Output:
4 5 6 1 2 3Prvé číslo vstupu je \(n=3\). Následne je na vstupe prvá trojica \((1, 2, 3)\) a potom druhá trojica \((4, 5, 6)\). Na výstup preto najskôr vypíšeme druhú trojicu a až potom prvú.
- (2 body) Na vstupe je číslo \(n\) a potom \(n\) čísel. Za nimi sú dve čísla \(a\) a \(b\) \((1\leq a\leq b\leq n)\). Na výstup vypíšte súčet čísel medzi \(a\)-tym až \(b\)-tym číslom (vrátane).
Input:
5 1 4 3 3 5 2 4Output:
10Na vstupe je 5 čísel, my máme vypísať súčet čísel od druhého po štvrté. To znamená \(4+3+3=10.\)
- (3 body) Na vstupe je \(n\) čísel \((n\geq 2)\). Vypíšte najmenšie a druhé najmenšie číslo.
Input:
4 8 1 5 -6Output:
-6 1- (3 body) Na vstupe je \(n\) čísel \((n \geq 1)\). Vypíšte číslo, ktoré je na vstupe najviac krát. Môžete predpokladať, že na vstupe je také číslo vždy jednoznačné.
Input:
3 2 5 3 1 2 3Output:
3- (5 bodov) Na vstupe je \(n\) čísel \((n \geq 1)\). Vypíšte všetky tieto čísla zoradené od najmenšieho po najväčšie.
Input:
3 -1 2 7 -4 5 -6Output:
-6 -4 -1 2 3 5 7Vzorové programy nájdete aj na stránke s editorom ksp.sk/~prask/specialne/4/2/3, kde si môžete odsimulovať ich beh. Pri čítaní vzorového riešenia odporúčame si to aj vyskúšať. Hoci vám slovne načrtneme základné myšlienky, predsa len je to prehľadnejšie, keď sa to aj hýbe.
Podúloha a.
Na vstupe je číslo \(n\) a potom dva krát \(n\) čísel. Na výstup vypíšte najskôr druhých \(n\) čísel a po nich prvých \(n\) čísel.
Riešenie tejto úlohy sa skladá z troch častí. Načítame prvú polovicu, načítame a vypíšeme druhú polovicu a na koniec vypíšeme prvú polovicu.
Prvá časť (modrá) načítava \(n\) čísel a ukladá ich do pamäte. Posledný príkaz v riadku je tam aby preskočil načítanie čísla \(n\), ktoré sme použili na začiatku. Šípka o riadok nižšie kompenzuje otočenie, ktoré spôsobí príkaz nad ňou, keď nemá čo uložiť do \(N\) (keď preskočíme načítanie pred ním).
Druhá časť (zelená) načítava a rovno vypisuje druhú polovicu čísel. Nasleduje krátky žltý úsek, ktorý pripraví hodnoty v \(N\) a \(A\) pred treťou časťou.
Tretia časť (červená) vypíše \(n\) čísel z pamäte a ukončí program.
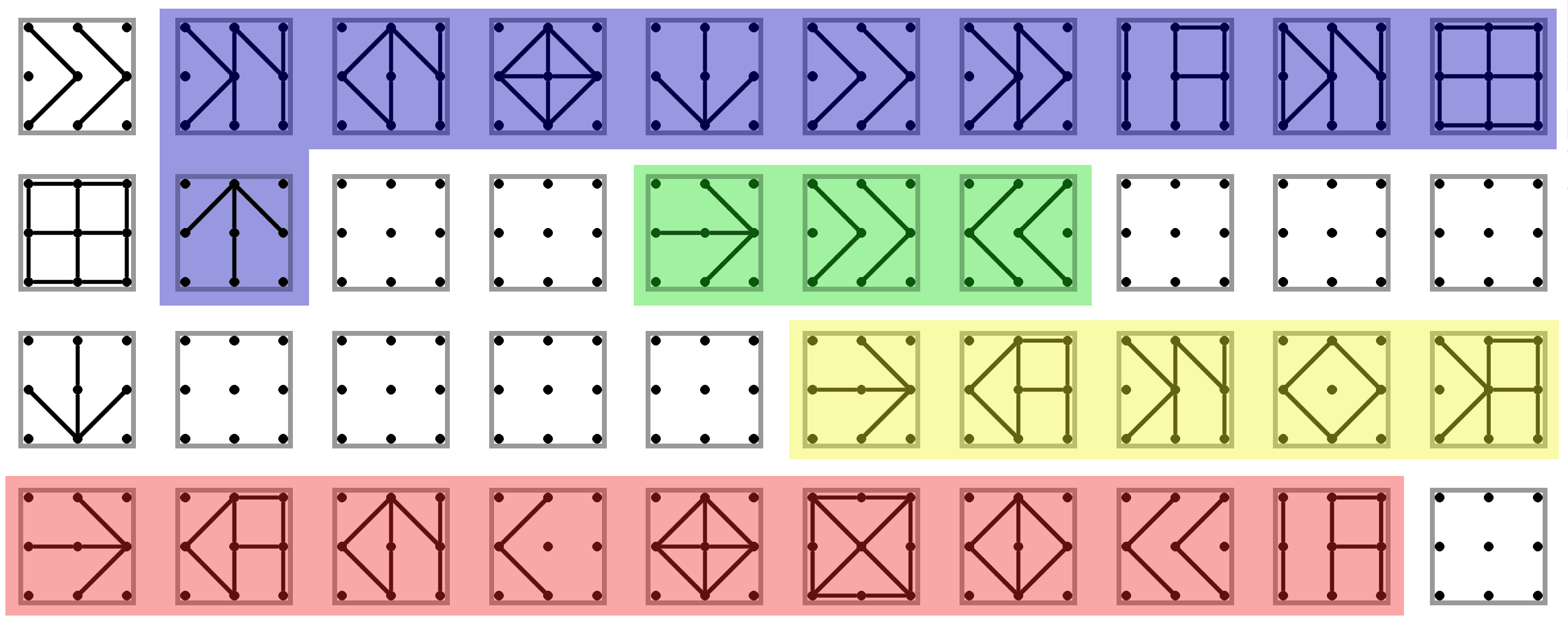
Podúloha b.
Na vstupe je číslo \(n\) a potom \(n\) čísel. Za nimi sú dve čísla \(a\) a \(b\). Na výstup vypíšte súčet čísel medzi \(a\)-tym a \(b\)-tym číslom (vrátane).
Zadanie začína podobne ako predošlá úloha. Vďaka tomu môže aj náš program začínať rovnako. Prvá časť (modrá) je preto úplne rovnaká.
V druhej časti (žltá) nám tento krát stačí načítať len dve čísla, preto žiadny cyklus.
V tretej časti budeme zväčšovať číslo v \(A\), ktoré zároveň určuje miesto v pamäti, až kým sa dostaneme na číslo v \(B\). V každom kole ešte pripočítame obsah \(D\) do \(I\), v ktorom bude na konci súčet celého úseku.
Na koniec (červená) už len vypíšeme obsah \(I\).
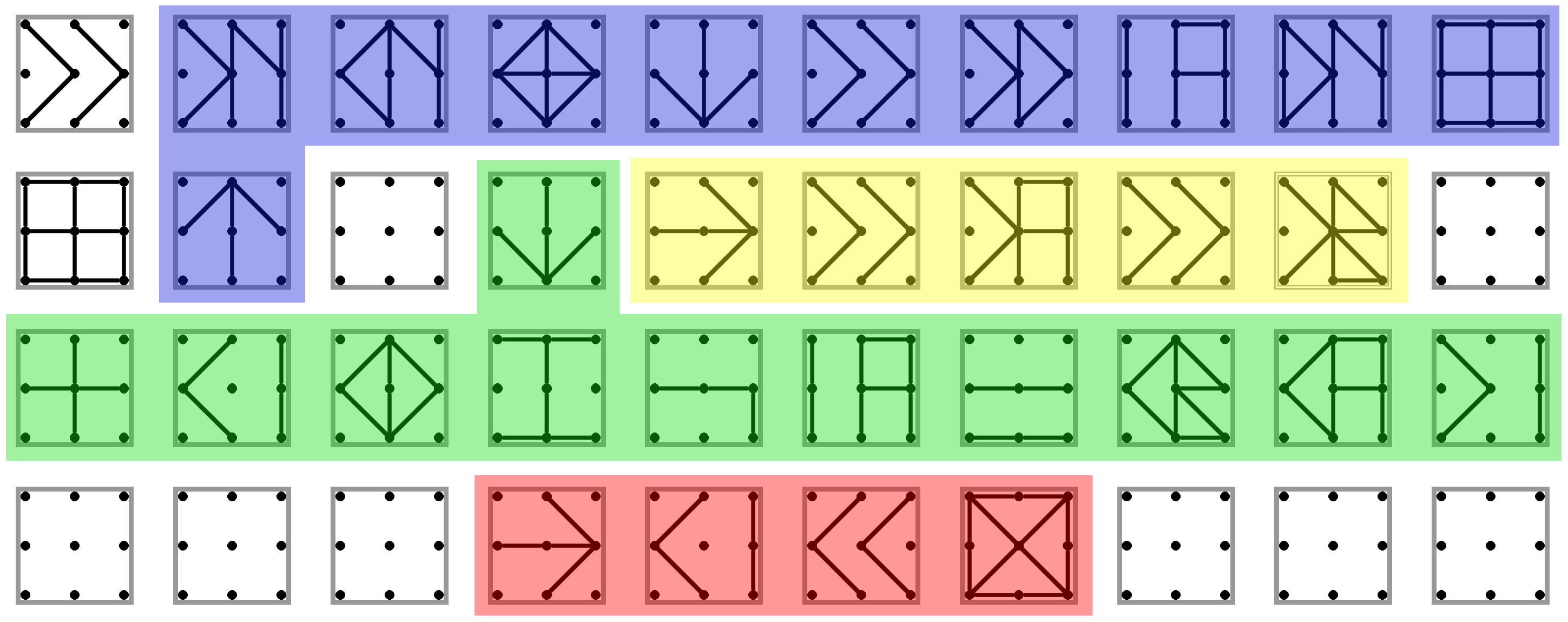
Podúloha c.
Na vstupe je \(n\) čísel. Vypíšte najmenšie a druhé najmenšie číslo.
Jednou z možností ako riešiť túto úlohu je vyriešiť podúlohu e. a mierne ju upraviť. Dá sa to však aj oveľa jednoduchšie a dokonca nepotrebujeme ani pamäť. Stačia nám dva registre. Budeme používať \(A\), kde bude najmenšie číslo a \(B\), kde bude druhé najmenšie.
Ako prvé (modrá) musíme do týchto registrov niečo uložiť, aby sme nepracovali s nulou, ktorá tam je na začiatku. Použijeme prvé dve čísla na vstupe.
Následne prejdeme do žltej časti, ktorá skontroluje, či v \(A\) nieje väčšie číslo ako v \(B\), a prípadne ich vymení. Keď ich vymení, podmienka bude už splnená, čiže sa to zopakuje najviac dva krát.
Vždy keď skončí žltá časť, prejdeme do zelenej, ktorá postupne načítava zvyšok vstupu. Každé číslo po načítaní zduplikujeme a porovnáme s \(B\). Ak je menšie, znamená to, že je jedným z dvoch doteraz najmenších tak ním prepíšeme \(B\). Po takejto zmene opäť prejdeme do žltej časti.
Ak načítané číslo nie je menšie, vymažeme jeho druhú kópiu a pokračujeme na ďalšie.
Nakoniec, keď sa minú čísla na vstupe, (červená) už len vypíšeme \(A\) a \(B\).
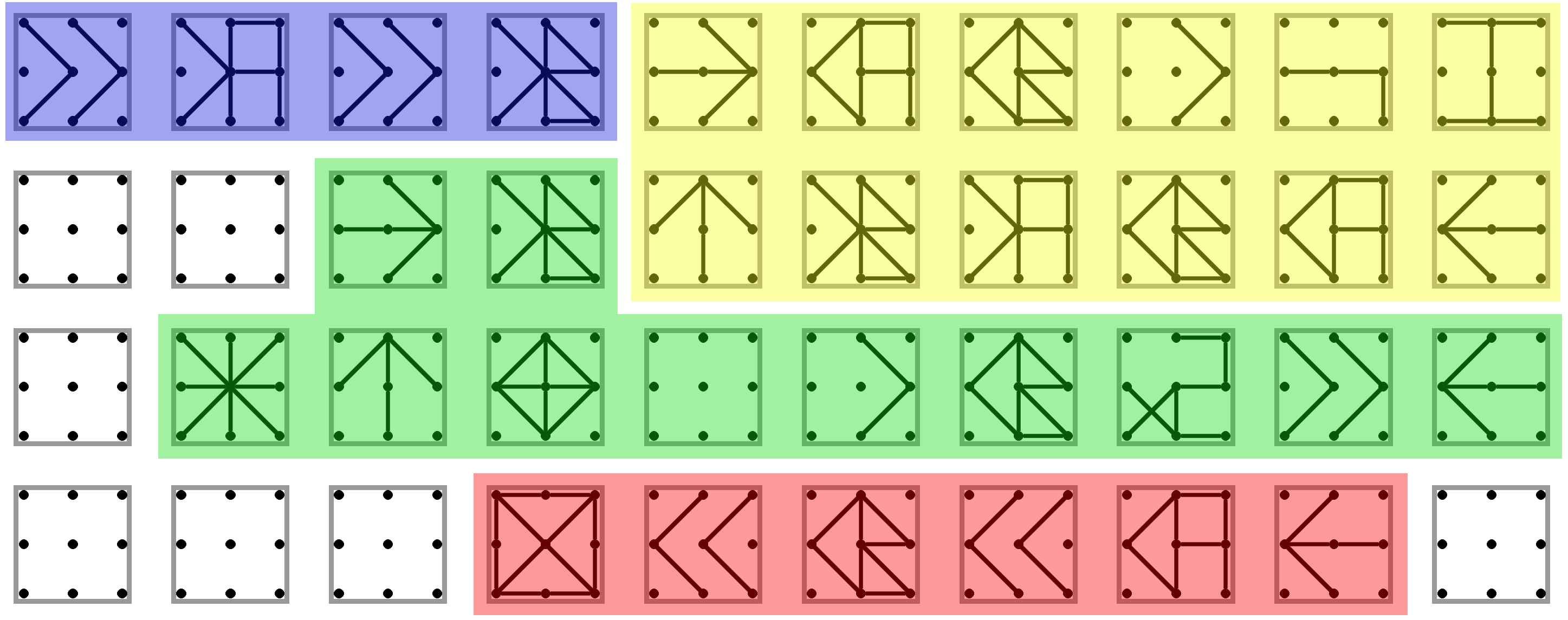
Podúloha d.
Na vstupe je \(n\) čísel. Vypíšte číslo, ktoré je na vstupe najviac krát.
Jedno z možných riešení, je opäť použiť riešenie podúlohy e, a v utriedenej postupnosti nájsť najdlhší úsek rovnakých čísel. Existuje však aj oveľa elegantnejšie riešenie, ktoré využíva úplne iný prístup ako predošlé úlohy.
Tento prístup sa líši v tom, že namiesto toho aby sme si čísla zo vstupu ukladali do pamäte, budeme ich používať ako adresu do pamäte a v pamäti bude hodnota koľko krát sme dané číslo už videli (modrá časť). Aby sme sa k týmto hodnotám dostali aj po tom, ako čísla načítame, budeme si všetky čísla zo vstupu kopírovať a ukladať na zásobník.
Keď máme takto načítaný vstup, dostávame sa k druhej časti (zelená), kde prechádzame cez všetky čísla na zásobníku a hľadáme to, ktoré sa na vstupe objavilo najviac krát. Keď nájdeme číslo, ktoré bolo na vstupe viac krát ako to, ktoré si pamätáme, pokračujeme na žltú časť, kde si uložíme do \(B\) koľko krát to bolo a do \(R\) aké číslo to bolo. Keď sa nám minú čísla na zásobníku, určite sme našli to, ktoré sa vyskytlo najviac krát. Preto prejdeme na červenú časť a vypíšeme hodnotu z \(R\).
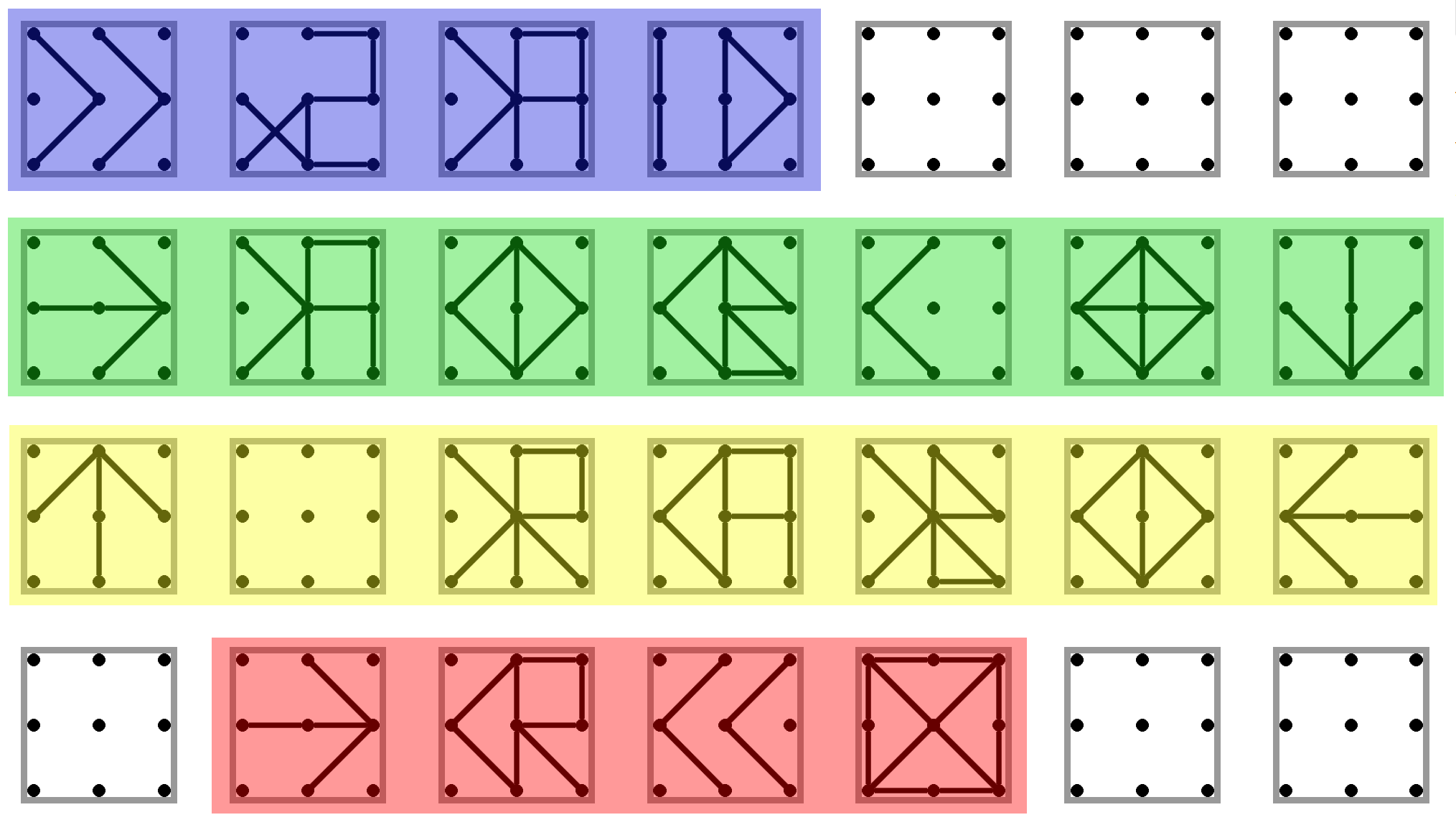
Podúloha e.
Na vstupe je \(n\) čísel. Vypíšte všetky tieto čísla zoradené od najmenšieho po najväčšie.
Zoradiť čísla je úloha ktorá sa v informatike vyskytuje veľmi často a preto ľudia vymysleli veľa spôsobov ako to spraviť1. Niektoré sú pomalšie a niektoré rýchlejšie. Nám viac záleží na jednoduchosti ako na rýchlosti, preto sme si vybrali Insertsort.
Jeho názov je odvodený od slova insert (vložiť), pretože postupne pridáva ďalšie a ďalšie číslo do už zoradenej postupnosti.
Náš program bude zoraďovať čísla v našej postupnosti od konca. Znamená to, že sa najprv budeme pozerať iba na posledné číslo. To je samo o sebe v správnom poradí (nemá na výber). Potom k nemu pridáme predposledné, to pred ním, až po to prvé. Predstavme si, že už máme nejakú postupnosť zoradenú a chceme do nej pridať ďalšie číslo. Nové číslo máme na začiatku tejto postupnosti. Porovnáme ho s číslom za ním. Ak je väčšie, znamená to, že má byť až za ním – vymeníme ich. Opäť sa pozrieme na naše nové číslo a to za ním a prípadne ich vymeníme a opakujeme. Keď narazíme na to, že ďalšie číslo je väčšie, znamená to, že aj čísla za ním budú väčšie, a čísla pred našim číslom musia byť menšie, keďže sme ich preskočili. Poradie pôvodných čísel sme nezmenili a nové číslo je na správnom mieste – máme zoradenú postupnosť.
Program sme rozdelili na \(5\) častí. Prvá a najjenoduchšia z nich (modrá) opäť slúži len na načítanie vstupu a posledná (červená) vypíše utriedené čísla z pamäte.
Fialová časť skontroluje, či je číslo v pamäti väčšie ako číslo pred ním. Ak je, znamená to, že ich treba vymeniť a prejdeme na žltú časť. Inak, ak je menšie alebo rovnaké, posunieme sa o jedno dozadu a pokračuje na zelenú časť.
Žltá časť vymení číslo v pamäti s tým ktoré je pred ním, posunie sa o jedno ďalej a pokračuje na zelenú.
Zelená časť dáva pozor na to, či sme sa neposunuli príliš ďaleko, ale aj na to, či sme sa ešte nedostali na začiatok. Ak sme sa dostali za koniec poľa, znamená to, že sme vymieňali posledné dve čísla a teraz sú už v správnom poradí. Preto nám stačí adresu zmenšiť o \(1\) a vrátiť sa tak ku poslednému číslu. O ostatné sa už postará fialová časť. Ak sme sa dostali na začiatok poľa, fialová časť musela skontrolovať všetky čísla, čiže máme usporiadané pole a môžeme čísla vypísať. Vtedy prejdeme na červenú časť.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.