Zadanie
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Dávidovi na [email protected]
Tomi išiel domov zo školy, a rozmýšľal, čo by robil, ak by sa dostal na opustený ostrov. Založil by si oheň, ulovil ryby, postavil príbytok, … Keď si už myslel, že má všetko premyslené a nič ho neprekvapí, uvedomil si, že by nemal ako programovať. A keby si aj začal písať programy na drevo, nemal by ako zistiť, či niekde neurobil chybu. Tomi by bez programovania neprežil, a preto si povedal, že vymyslí nový programovací jazyk, ktorý bude pohodlný, bude sa ľahko kresliť na drevo a bude sa dať ľahko ručne simulovať jeho vykonávanie. Nazval ho Kreslo (pretože sa kreslí a je pohodlný). Tomi by rád vedel, ako dobrý je jeho jazyk a čo všetko sa v ňom dá naprogramovať. Na to potrebuje vašu pomoc.

Úloha
Kreslo je veľmi jednoduchý jazyk. Pracuje iba s celými číslami, ktoré vie načítavať zo vstupu a vypisovať na výstup. Aby sa Tomimu ľahko kreslilo, celý program je nakreslený do mriežky a každá inštrukcia zaberá jeden štvorec. Podrobnosti o tom, ako tento jazyk funguje a ako v ňom písať programy nájdete na ksp.sk/~prask/specialne/4/1/3/manual.pdf
My našťastie nie sme na opustenom ostrove, a preto môžeme používať elektronický editor, ktorý dokáže aj simulovať beh programu. Nájdete ho spolu s ukážkovými programami na adrese ksp.sk/~prask/specialne/4/1/3/.
Vašou úlohou bude vyriešiť nasledujúce podúlohy a odovzdať ZIP súbor, ktorý obsahuje zdrojové kódy vašich riešení (dajú sa stiahnuť z editora). ZIP by mal obsahovať súbory 1.kr až 5.kr s vašimi riešeniami jednotlivých podúloh.
Podúlohy
- (1 bod) Na vstupe je zadané číslo \(a\) \((1 \leq a \leq 1\,000)\). Vypíšte číslo \(7\) ak \(a\) je deliteľné číslom \(7\) (je to násobok sedmičky), inak vypíšte číslo \(a\) nezmenené.
Input:
21Output:
7Input:
47Output:
47- (3 body) Na vstupe je zadané číslo \(n\) \((1 \leq n \leq 100)\). Vypíšte čísla od \(n\) do \(1\) v klesajúcom poradí.
Input:
7Output:
7 6 5 4 3 2 1- (4 body) Na vstupe sú zadané čísla \(x\) a \(y\) \((0 \leq x \leq y \leq 100)\). Vypíšte v rastúcom poradí všetky čísla od \(x\) do \(y\) (vrátane), ktoré sú násobkami čísla \(3\).
Input:
39 47Output:
39 42 45- (4 body) Na vstupe je zadané číslo \(n\) \((1 \leq n \leq 1000)\). Vypíšte najmenšie číslo \(a\), \(1 < a \leq n\) ktoré delí \(n\) (zvyšok po delení \(n\) číslom \(a\) je \(0\)).
Input:
35Output:
5Deliteľmi čísla 35 sú čísla 1, 5, 7 a 35. Keďže 1 vypísať nemôžeme, najmenší deliteľ je číslo 5.
(3 body) Prvočísla sú prirodzené čísla väčšie ako 1, ktoré nie sú deliteľné žiadnym číslom od 2 po \(p-1\). Napríklad čísla 2, 5, 7, 23 sú prvočísla, čísla 1, 4, 50, 99 nie sú.
Na vstupe je zadané číslo \(n\) \((2 \leq n \leq 100)\). Vypíšte všetky prvočísla z rozsahu od \(2\) po \(n\) v rastúcom poradí.
Input:
11Output:
2 3 5 7 11Vzorové programy nájdete aj na stránke s editorom ksp.sk/~prask/specialne/4/1/3 kde si môžete odsimulovať ich beh. Pri čítaní vzorového riešenia odporúčame si to aj skúšať. Hoci vám slovne načrtneme základné myšlienky, predsa len je to prehľadnejšie, keď sa to aj hýbe.
Podúloha a.
Na vstupe je zadané číslo \(a\). Vypíšte číslo \(7\) ak je \(a\) deliteľné číslom \(7\) (je to násobok sedmičky), inak vypíšte číslo \(a\) nezmenené.
Na vyriešenie prvej podúlohy stačí pochopiť ako fungujú jednotlivé inštrukcie. Následne existuje niekoľko veľmi podobných riešení. Každé však začína tým, že načítame vstup. Načítanú hodnotu si ale potrebujeme niekam uložiť. Na to môžeme použiť buď niektorý z registrov alebo zásobník. My si ukážeme riešenie pomocou zásobníka. Číslo zo vstupu zduplikujeme (aby tam jedna kópia ostala aj po kontrole deliteľnosti), na zásobník pridáme číslo \(7\) a spravíme operáciu modulo. Následne pridáme podmienený skok, vďaka ktorému dáme číslo \(7\) na vrch zásobníka, iba ak vyšiel zvyšok nula. Ak zvyšok nie je \(0\), táto inštrukcia sa preskočí a na vrchu zásobníka bude pôvodné číslo zo vstupu. Ostáva vypísať číslo, ktoré je na vrchu zásobníka a ukončiť program.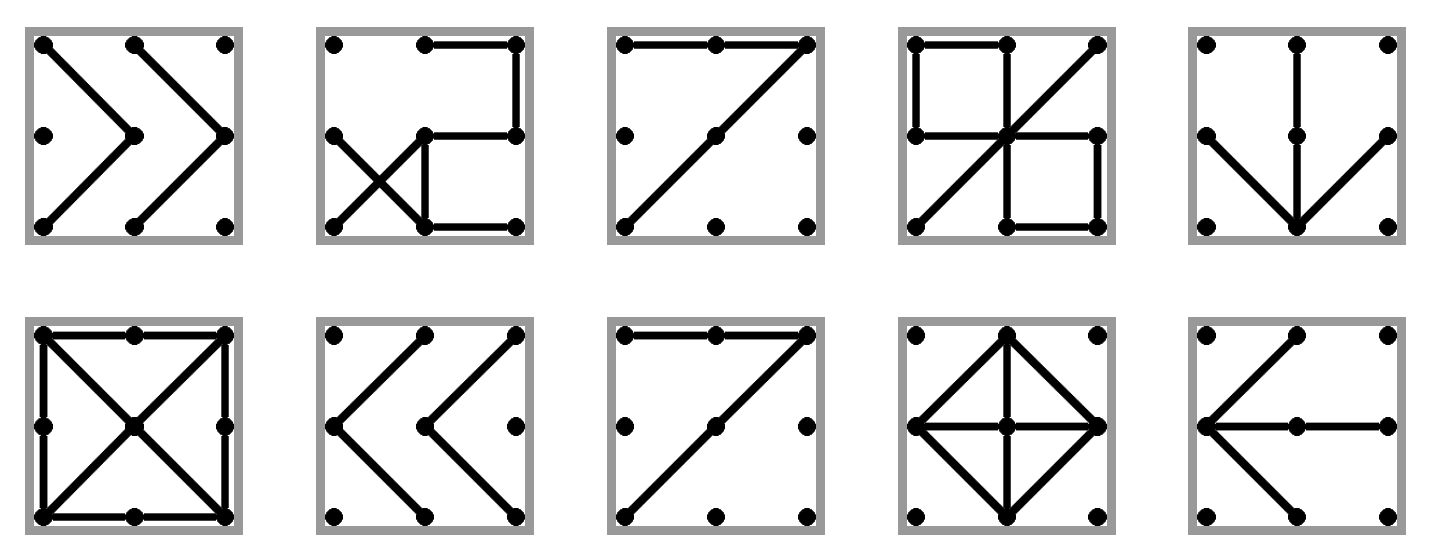
Podúloha b.
Na vstupe je zadané číslo \(n\). Vypíšte čísla od \(n\) po \(1\) v klesajúcom poradí.
Pri riešení tejto podúlohy musíme časť nášho programu opakovať. To vieme dosiahnuť pomocou šipiek, vo vzorovom riešení sa však používa aj nasledovný trik – keďže na vstupe je len jedno číslo, tak keď sa náš program ocitne druhýkrát na príkaze na načítanie vstupu, tak nič nenačíta (lebo nemá čo) a iba sa otočí o \(90°\) doprava. Túto inšrukciu budeme preto “recyklovať” – prvý krát ju použijeme na načítanie vstupu a následne ju budeme používať ako šipku doprava.
Vyriešiť úlohu je už potom ľahké. Na zásobníku (alebo v registri) si pamätáme aktuálne číslo, ktoré máme vypočítať. Podmieneným skokom overíme, či toto číslo nie je 0. Ak áno, program ukončíme. Inak číslo zduplikujeme a kópiu navrchu vypíšeme. Potom pridáme 1 a znamienko mínus zmenší číslo na zásobníku (v registri). V tomto momente môžeme celý proces začať odznovu.
So zásobníkom: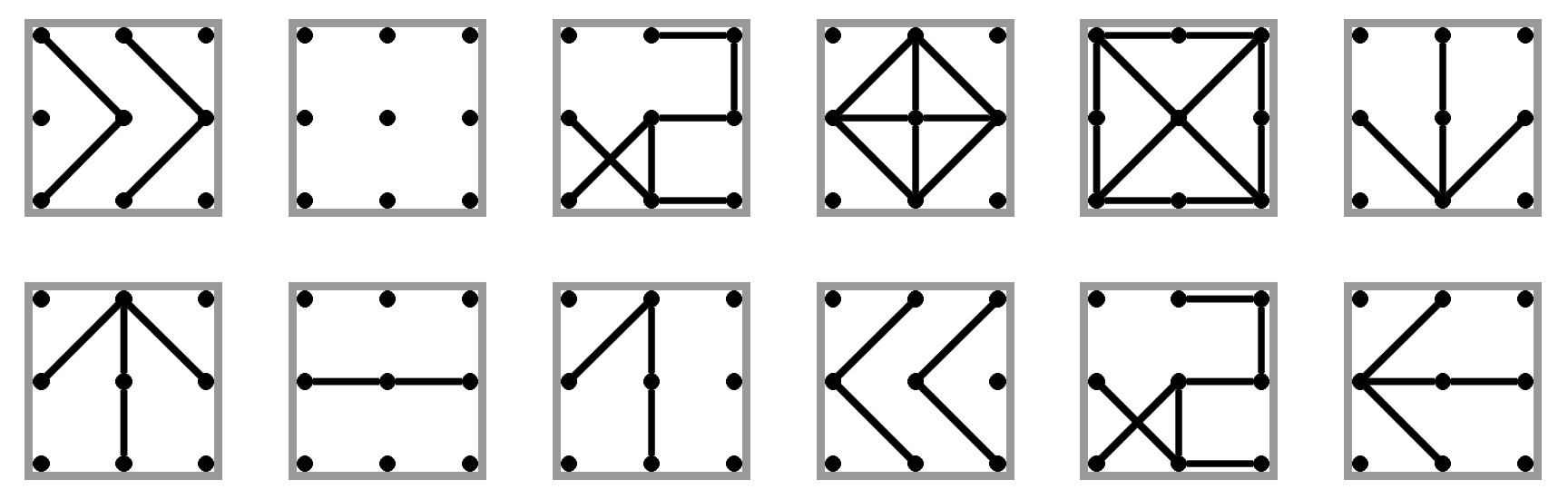
S registrom:
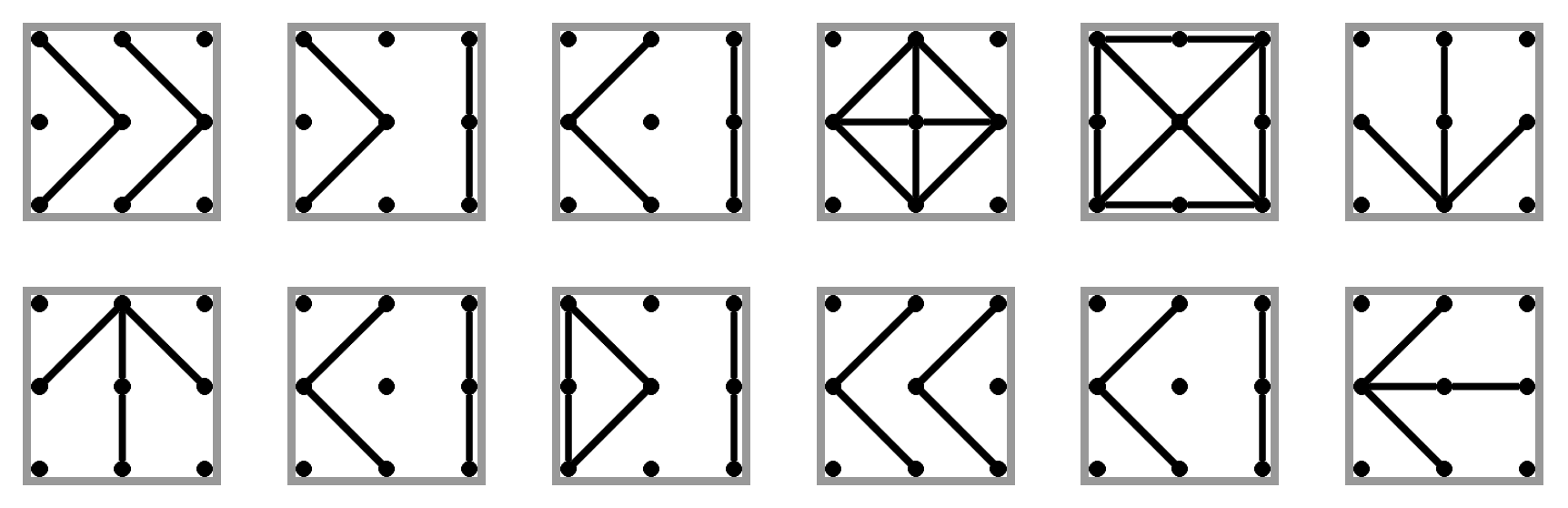
Podúloha c.
Na vstupe sú zadané čísla \(x\) a \(y\). Vypíšte v rastúcom poradí všetky čísla od \(x\) do \(y\) (vrátane), ktoré sú násobkami čísla \(3\).
Táto úloha sa dá vyriešiť jednoduchou úpravou predošlého riešenia. Pri každom opakovaní iba navyše overíme, či je dané číslo deliteľné troma.

Ukážeme si však ešte jedno riešenie. Je síce o niečo zložitejšie, ale o to krajšie. Namiesto toho, aby sme prechádzali všetkými číslami, budeme prechádzať iba násobkami čísla 3.
Samozrejme, je problém, ak číslo \(x\) nie je na začiatku násobok 3. Preto ho ešte pred začiatkom zväčšíme na najbližší väčší násobok 3 pomocou jednoduchého cyklu, ktorý sa bude opakovať, kým nebude zvyšok po delení čísla \(x\) nula. Po zväčšení čísla \(x\) načítame druhé číslo zo vstupu do registra A a začneme samotný cyklus vypisovania. Ten začneme tým, že overíme, že hranica v registry A ešte nebola prekročená. Ak nie, vypíšeme \(x\) a následne ho zväčšíme o 3, čím sa posunieme rovno na ďalší násobok 3.
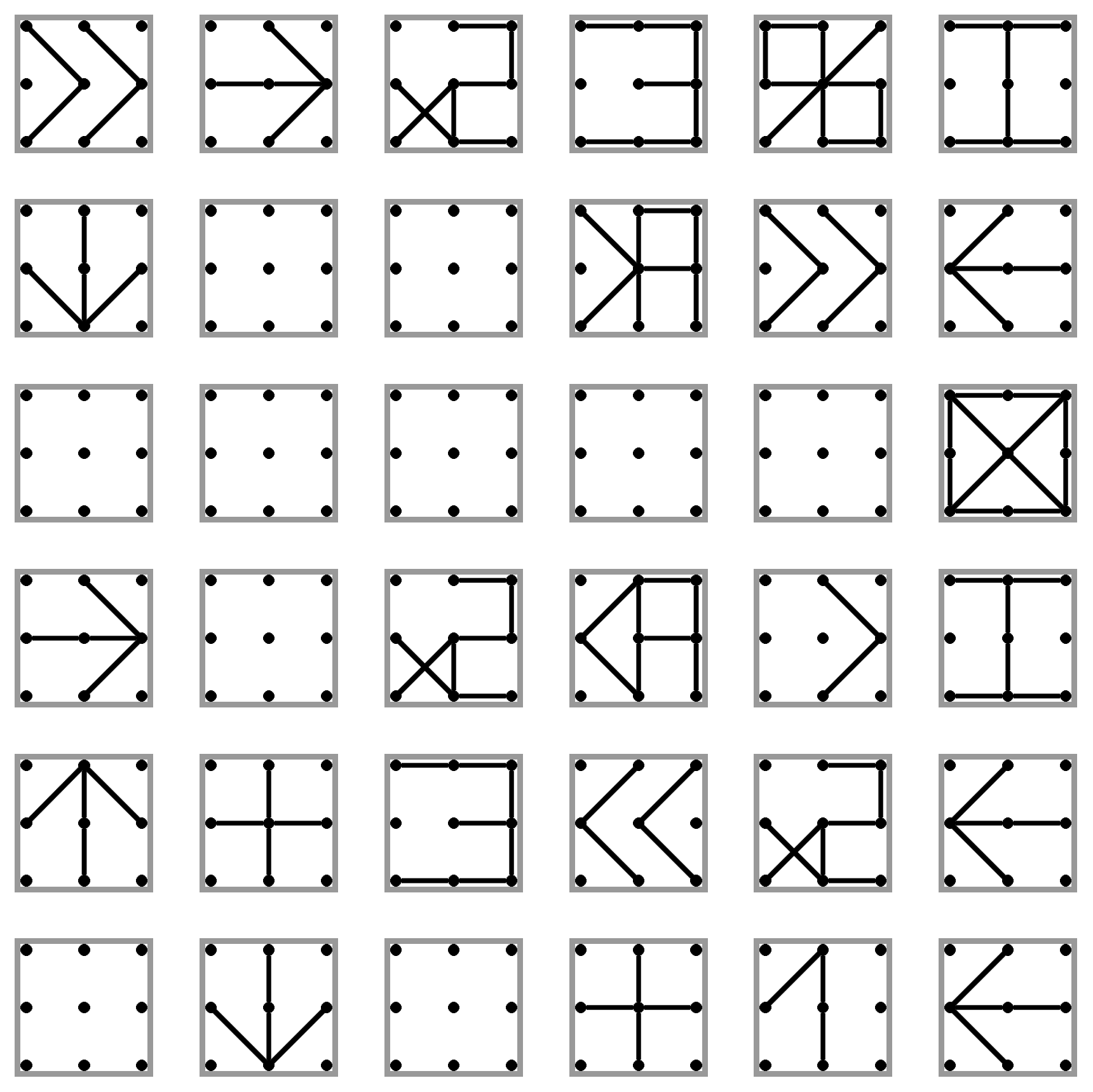
Podúloha d.
Na vstupe je zadané číslo \(n\). Vypíšte najmenšie číslo \(a\), \(1 < a\) ktoré delí \(n\) (zvyšok po delení \(n\) číslom \(a\) je \(0\)).
Opäť jednoduchšia úloha, riešením je jeden cyklus, v ktorom hľadáme najmenšieho deliteľa. Stačí postupne zväčšovať jedno číslo (pozor, aby sme začínali na dvojke a nie na jednotke) a v okamihu, keď toto číslo delí \(n\) vypísať ho a ukončiť program. No a overenie deliteľnosti nejakým číslom sme predsa už robili v podúlohe a. aj c..
Podúloha e.
Na vstupe je zadané číslo \(n\). Vypíšte všetky prvočísla z rozsahu od \(2\) po \(n\) v rastúcom poradí.
Na vyriešenie tejto úlohy treba spojiť riešenia podúloh c. a d.. Budeme mať vonkajší cyklus, ktorý prechádza postupne všetkými číslami a vnútorný cyklus, ktorý pre dané číslo nájde najmenšieho deliteľa. Potom nám stačí skontrolovať, či sa tento deliteľ rovná nášmu číslu. Ak áno, dané číslo je prvočíslo a môžeme ho vypísať. V opačnom prípade pokračujeme na ďalšie číslo.

Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.