1. Premiestnení faraóni vzorové riešenie

Zadanie

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Andrejovi na

Egypťania sa tento rok rozhodli spraviť rozsiahlu rekonštrukciu pyramíd. Potrebujú preto premiestniť všetkých faraónov do jednej veľkej spoločnej pyramídy. Na samý vrch tejto pyramídy uložia ich najobľúbenejšieho faraóna a zvyšných dajú do miestností pod ním. Keďže nová pyramída ešte nestojí a my nevieme, koľko poschodí bude mať, poschodia budeme číslovať od vrchu, začínajúc poschodím číslo 1.

Ich cieľom je uložiť do tejto pyramídy čo najviac faraónov. Rozhodli sa preto, že len čo ju postavia, začnú ju zvrchu postupne napĺňať. Tu však narazili na dva problémy. Z dôvodu hmostnosti starovekých sarkofágov môžu do ktorejkoľvek miestnosti vložiť faraóna, len ak sa priamo nad ním nenachádzajú dvaja iní faraóni. Navyše faraóni sú spoločenské bytosti, preto musí priamo nad každým faraónom (s výnimkou hlavného faraóna na vrchu pyramídy) ležať aspoň jeden iný faraón.

Postup napĺňania teda vyzerá nasledovne: prechádzame postupne po poschodiach všetky izby, pričom začíname najvyšším poschodím. Ak sa priamo nad danou izbou nachádzajú dvaja faraóni, alebo tam naopak žiaden faraón nie je, izba ostane prázdna. V opačnom prípade (teda priamo nad izbou je jeden faraón) tam vložíme ďalšieho faraóna.

Na nasledujúcom obrázku je príklad pyramídy so šiestimi poschodiami, ktorá bola zaplnená práve takýmto spôsobom.

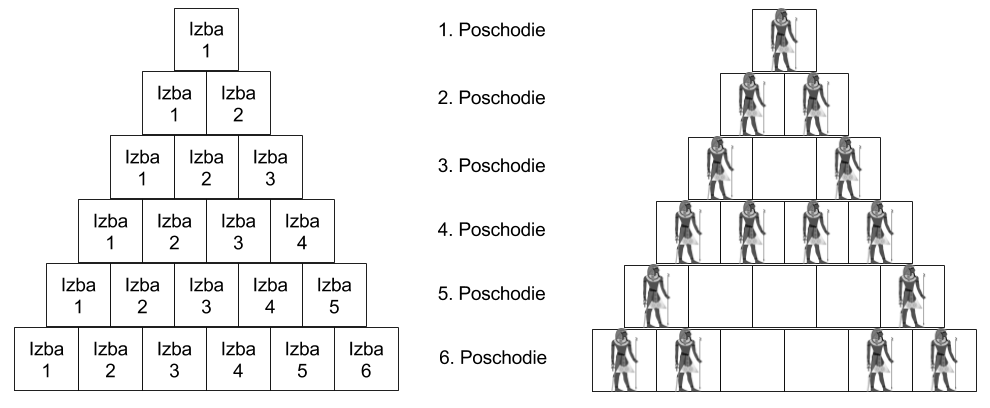
Vidíme, že v izbe 2 na 3. poschodí nie je umiestnený faraón a to preto, že obe izby nad ním sú plné. Toto nastalo aj v troch izbách na 5. poschodí. V izbe 3 na 6. poschodí taktiež nie je faraón a to preto, že mu nad ním v izbách 2 a 3 na 5. poschodí chýba spoločnosť. Toto platí aj o izbe 4 na 6. poschodí.

V izbe 2 na štvrtom poschodí však faraón je, lebo nad ním je práve jeden iný faraón (izba 1, 3. poschodie). Takisto si všimnite, že v izbe 1 je na každom poschodí faraón, lebo nad ním môže byť iba jeden faraón a ten tam vždy je.

Uvedeným spôsobom vieme vyplniť ľubovoľne veľkú pyramídu. Odporúčame vám si to vyskúšať napríklad na papier a nakresliť si, ako by vyzerala pyramída, ktorá by mala o niečo viac poschodí.

Úloha

1. (4 body) Na obrázku vyššie môžeme vidieť, že na 4. poschodí ja každá izba obsadená faraónom. Ešte pred postavením pyramídy by architektov zaujímalo, či je počet takýchto plne obsadených poschodí obmedzený alebo nie. Vyššie uvedenú pyramídu by sa totiž rozhodne neoplatilo postaviť 3 poschodovú keďže práve 4. poschodie vieme celé naplniť.

   Vašou úlohou je zistiť, či sa podobný riadok v pyramíde vyskytuje aj na spodnejších poschodiach. Pre zjednodušenie si predstavte, že túto pyramídu sme postavili nekonečne vysokú. Platí, že sa tam pri plnení zhora vždy po istej dobe takéto poschodie plné faraónov znova vyskytne? Ak áno, vedeli by ste nájsť pravidlo, ktoré určí, či poschodie s poradovým číslom \(x\) je práve takéto poschodie? Obe svoje tvrdenia sa pokúste dokázať.

2. (6 bodov) Akonáhle bude pyramída dostavaná, bude staviteľov zaujímať, či do konkrétnej izby majú niekoho nasťahovať alebo nie. Z tohto dôvodu si musia byť istí, že viete o každej izbe správne určiť, či bude alebo nebude obývaná. Inak vám takúto dôležitú úlohu do rúk určite nemôžu zveriť.

   Vašou úlohou je zistiť, či bude izba číslo 10 na 20. poschodí obývaná alebo nie. Toto isté zistite aj o izbe číslo 266 na poschodí 276. K vašej odpovedi by ste mali napísať aj popis vášho riešenia, teda ako ste sa k tomuto výsledku dopracovali.

3. (5 bodov) Po preverení vašich schopností sa už môžete pustiť do práce. Pyramída sa medzičasom postavila a vy ste dostali za úlohu vymyslieť postup, vďaka ktorému vieme o ľubovolnej izbe povedať, či bude alebo nebude obývaná. Egypťanom však došiel papyrus a tak by boli veľmi radi, ak by ste vymysleli šetrnejší spôsob ako kreslenie si celej pyramídy.

   Vašou úlohou je vymyslieť postup, ktorý určí pre ľubovolné poschodie a izbu na tomto poschodí, či v nej bude alebo nebude faraón a to v čo najmenšom počte krokov. Vzorové riešenie by bolo schopné zistiť zaplnenosť ktorejkoľvek izby aj na poschodí s číslom rádovo okolo \(1\,000\,000\) (a aj omnoho viac) a to len s použitím papiera a rozumného množstva času. Upozorňujeme, že okrem vysvetlenia tohto postupu na nejakom príklade musíte uviesť jednoznačný postup, ktorý vie opravovateľ na ktoromkoľvek inom poschodí a izbe zopakovať a dopracovať sa k správnemu výsledku.

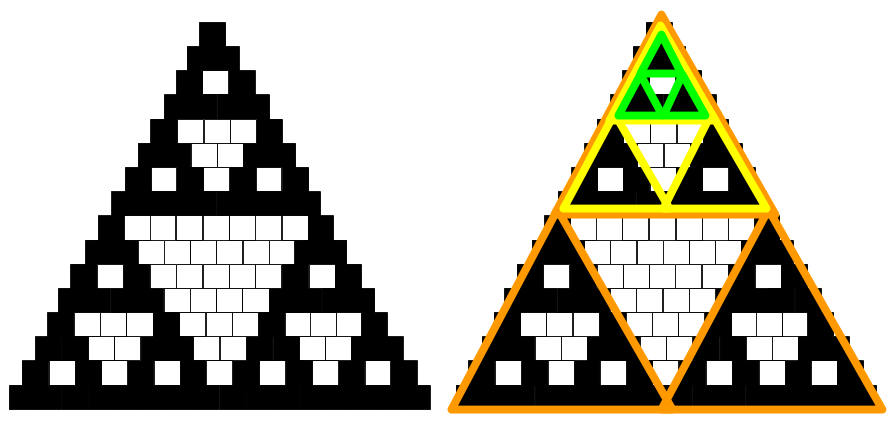
Prvá vec, ktorá by nám mohla pri riešení tejto úlohy pomôcť je, že si nakreslíme o niečo väčšiu pyramídu a pozrieme sa, ako vyzerá. Miesta, kde sa nachádzajú faraóni si budeme značiť čiernym štvorčekom a miesta kde nie sú bielym.

Zopakujme si najskôr pravidlá pre stavbu pyramídy. V najvyššej miestnosti sa musí nachádzať faraón. Následne, miestnosť pod dvoma obsadenými a tiež dvoma prázdnymi izbami musí byť prázdna. Sarkofág s faraónom teda budeme ukladať iba do izieb, ktoré majú nad sebou jednu plnú a jednu prázdnu izbu. Všimnite si tiež, že okolie pyramídy si môžeme predstaviť ako prázdne izby a napĺňanie miestností bude bez problémov fungovať.

Podúloha a.

Keď sa pozrieme na obrázok, môžeme si všimnúť niekoľko vecí. Jedno z najľahších pozorovaní je, že na \(n\)-tom poschodí sa nachádza presne \(n\) izieb. Ako oveľa zaujímavejšie sa však javia vzory, ktoré sa nám v našej pyramíde vytvorili. Presnejšie, pod každým poschodím, ktoré je vyplnené faraónmi, sa nachádzajú dve kópie doterajšej pyramídy – jedna naľavo a jedna napravo. A medzi týmito dvoma kópiami je prázdny priestor. Toto si môžete všimnúť jednak na riadku 4 a riadku 8.

Samozrejme, obrázok so 16 poschodiami nie je dôkaz toho, že to tak musí byť. Dáva nám to však najavo, že ideme dobrým smerom.

Začnime tým, že si zoberieme jedno poschodie, ktoré je vyplnené sarkofágmi. Ako vyzerá poschodie pod ním? Keďže pod dvoma susednými sarkofágmi nemôže ležať tretí, všetky miestnosti, okrem dvoch krajných budú prázdne. No a tieto dve krajné miestnosti by mali tvoriť vrch našich dvoch nových pyramíd.

A naozaj, keď si zoberieme jedno z nich, tak vedľa neho sú prázdne miestnosti a preto budú izby pod ním vyzerať ako v druhom riadku celej pyramídy. A opäť, na jednej strane tohto ďalšieho riadku je okraj pyramídy a na druhom prázdne izby (pretože pod dvoma prázdnymi izbami je opäť prázdna izba) a miestnosti pod ním sa vyplnia rovnako ako v treťom riadku pyramídy.

Keby nám takto vznikala len jedna pyramídy, tak jej nič nebráni, aby vyzerala rovnako ako tá nad ňou. Nám sa však takto tvoria súčasne dve pyramídy. Kým sú ďaleko od seba, oddelené prázdnymi izbami, tak sa nijak neovplyvňujú. Ak však medzi nimi prázdne izby nebudú, tieto dve menšie pyramídy sa začnú ovplyvňovať.

Už z obrázka je jasné, že tieto dve pyramídy sa skutočne k sebe približujú. Kedy sa však stretnú? Uvedomme si, že každá pyramída sa v ďalšom riadku zväčší o 1 políčko. A obe menšie pyramídy sa postupne (a symetricky) posúvajú ku stredu. Obe sa teda posunú o jedno políčko do stredu, ale zároveň, celá veľká pyramída narastie na danom riadku o jednu miestnosť. Vzájomná vzdialenosť sa preto zmenší o jednu miestnosť.

Čo sa teda stane v našom prípade na poschodí 9 a nižšie? Pyramída, ktorá je tvorená ôsmimi poschodiami má spodné poschodie vyplnené faraónmi. Preto sa na deviatom poschodí začnú tvoriť dve menšie pyramídy. Tieto dve pyramídy na ich prvom poschodí (deviate celkovo) delí 7 (\(8-1\)) voľných izieb. Na ich druhom poschodí (desiate celkovo) ich delí o jednu izbu menej, teda 6 (\(8-2\)) izieb. To znamená, že sa stretnú na ich ôsmom poschodí (šestnáste celkovo), kde ich vzájomná vzdialenosť bude 0 (\(8-8\)) izieb.

A práve ôsme poschodie je predsa celé vyplnené faraónmi. To znamená, že celé šestnáste poschodie obsahuje iba faraónov – obe menšie pyramídy tu majú svoje ôsme poschodie a nie je medzi nimi žiadna prázdna izba.

Túto úvahu teraz vieme zopakovať aj pre pyramídu veľkosti 16. Na riadku 17 sa totiž začnú tvoriť dve pyramídy, ktoré budú oddelené 15-timi prázdnymi izbami. Dotknú sa preto na riadku 32, kde sa stretnú akurát dva riadky číslo 16 menších pyramíd, ktoré obsahujú iba faraónov, čo znamená, že aj riadok 32 obsahuje iba faraónov.

A takto to bude pokračovať aj ďalej, postupne s pyramídami veľkosti 64, 128, 256, 512… Ak si totiž zoberieme nejaký z týchto plných riadkov, tak dve menšie pyramídy, ktoré sa pod ním začnú vytvárať sa stretnú práve na riadku, ktorých je dvakrát väčší. Čísla úplne zaplnených poschodí budú teda v tvare \(1\), \(2\cdot 1 = 2\), \(2\cdot 2\cdot 1 = 4\), \(2\cdot 2\cdot 2 = 8\), \(2\cdot 2\cdot 2\cdot 2 = 16\), \(2\cdot 2\cdot 2\cdot2 \cdot 2 = 32\).

Tieto čísla sú takzvané mocniny dvojky a preto môžeme povedať, že čísla zaplnených poschodí majú tvar \(2^n\), pre \(n \geq 0\).

Podúloha b.

Riešenie podúlohy b. nebolo vôbec ťažké. Napríklad jej prvú polovicu, kde ste mali zistiť zaplnenosť miestnosti na dvadsiatom poschodí ste mohli vyriešiť jednoducho tým, že ste si to nakreslili. Druhú časť by sa vám však už rukou kresliť nechcelo, predsa len vyše 200 riadkov je veľa. Kreslenie našej pyramídy má však vcelku jasné, algoritmické pravidlá. Preto ste si buď mohli napísať krátky program, ktorý vám to vypočítal, poprípade použiť Excel¹.

Ak to chceme riešiť pomocou tabuľkového editoru, tak jedinou otázkou ostáva, ako vypočítať číslo, ktoré uložíme do bunky. Začneme tým, že si celú tabuľku zarovnáme doľava. Vtedy bude platiť, že každé políčko vieme vypočítať pomocou políčka priamo nad ním a políčka o jedna nad ním a doľava. No a naviac môžeme použiť funkciu MOD(a, 2), ktorá počíta zvyšok čísla \(a\) po delení 2. Ak totiž prítomnosť faraóna v miestnosti reprezentujeme číslom 1, tak keď sa pozrieme na súčet dvoch políčok nad bunkou, ktorú chceme vypočítať, chceme dostať súčet 1 a nechceme dostať súčet 0 a 2. Súčet 0 aj 2 majú však rovnaký zvyšok po delení 2 a to je 0. Naviac, tento zvyšok je presne číslo, ktoré chceme vložiť do našej bunky. Príklad takejto tabuľky je napríklad tu.

Vzorové riešenie tejto úlohy však nebolo kreslenie ani počítanie Excelom. Chcelo to len trochu sa zamyslieť a zároveň vás posunúť správnym smerom pred riešením podúlohy c.. Poďme si ešte raz preriešiť zadané dva príklady.

Poschodie 20, izba 10

Poschodia, ktoré sú tvaru \(2^n\) vieme riešiť hneď, pretože obsahujú iba faraónov. Bohužiaľ 20 nie je mocninou čísla 2. Najbližšia menšia mocnina čísla 2 je 16. A z podúlohy a. vieme, že pod týmto poschodím sa tvoria dve nové pyramídy. Poschodie 20 teda vyzerá tak, že obsahuje dve kópie poschodia 4 oddelené prázdnymi miestnosťami. Prvá kópia poschodia 4 je úplne naľavo na políčkach 1 až 4 (štvrté poschodie má štyri políčka). Druhá kópia je úplne napravo na políčkach 17 až 20. A políčka medzi tým, teda políčka 5 až 16 sú prázdne.

Z toho vyplýva, že izba 10 na poschodí 20 neobsahuje faraóna.

poschodie 276, izba 266

Číslo \(276\) opäť nie je mocninou \(2\), najbližšia menšia mocnina je 256. Poschodie 256 preto obsahuje iba faraónov. Poschodie 276 je preto tvorené dvoma kópiami riadku 20 oddelenými prázdnymi izbami. Ľavá kópia je na políčkach 1 až 20, pravá na políčkach 257 až 276. Izba 266 teda neleží v prázdnych izbách medzi nimi, ale patrí pravej kópii.

Presnejšie, je to izba číslo 10 pravej kópie riadku číslo 20 na poschodí 276. To ale znamená, že zistiť, či je v izbe 266 na poschodí 276 faraón je rovnaké, ako zistiť, či je faraón v izba 10 na poschodí 20. A to sme predsa už zistili v prechádzajúcom zadaní. V izbe 266 na poschodí 276 sa teda faraón nenachádza.

Podúloha c.

Pre riešenie podúlohy c. si vyššie popísaný postup zovšeobecníme. Nech \(p\) označuje číslo poschodia, \(c_i\) číslo izby a \(m_2\) najbližšiu mocninu čísla 2 menšiu ako \(p\).

Začnime tým, že si popíšeme ako vypočítať hodnotu \(m_2\). Začínajúc m_2 = 1 budeme toto číslo násobiť až do momentu, keď \(m_2 \geq p\). Týmto spôsobom narazíme na prvú mocninu 2, ktorá je väčšia alebo rovná číslu \(p\). Ak \(m_2\) následne vydelíme 2, ostane nám v tejto premennej hľadaná hodnota – najbližšia mocnina 2 menšia ako \(p\).²

Ako prvé overme, či je číslo \(p\) mocnina 2. V prípade, že je, vieme, že bez ohľadu na to, na akú izbu sa pýtame, tak v nej bude faraón. Keďže \(m_2\) je najbližšia mocnina menšia ako 2, tak \(p\) je mocnina 2 iba ak \(2m_2 = p\).

V opačnom prípade vieme, že pod riadkom \(m_2\) sa začali tvoriť dve menšie pyramídy a na riadku \(p\) sa nachádzajú ich v \(p-m_2\)-hé riadky. Tieto dve kópie sú dlhé \(p-m_2\), jedna je úplne naľavo, druhá úplne napravo a medzi nimi sú prázdne izby. Presnejšie izby s číslami 1 až \(p-m_2\) tvoria ľavú kópiu a izby s číslami \(p-(p-m_2)+1 = m_2 + 1\) až \(p\) tvoria pravú kópiu.

Môžeme preto overiť, či platí \((p - m_2) < c_i < (m_2 + 1)\). V takom prípade sa totiž v hľadanej izbe faraón určite nenachádza.

V opačnom prípade sa naša izba nachádza v jednej z dvoch menších pyramíd. Ak je v ľavej pyramíde (\(c_i \leq p-m_2\)), tak vieme, že pýtať sa na poschodie \(p\) a izbu \(c_i\) je to isté ako sa pýtať na poschodie \(p - m_2\) a izbu \(c_i\). Naopak ak je v pravej pyramíde, tak otázka na poschodie \(p\) a izbu \(c_i\) je rovnaká ako otázka na poschodie \(p-m_2\) a izbu \(c_i-m_2\). V oboch prípadoch však dostaneme výrazne ľahší problém, pretože hodnota poschodia, ktoré hľadáme sa nám výrazne znížila.

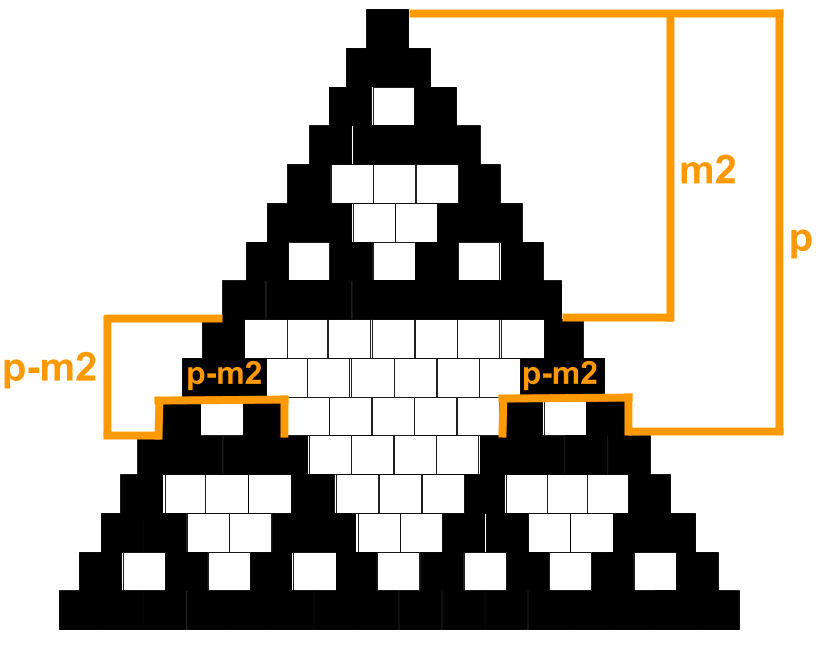
A tento istý postup môžeme opakovať. Stačí si pre nové poschodie \(p-m_2\) vypočítať novú hodnotu \(m_2\) a dostať ešte menší problém. A tento postup opakovať, až kým sa nedostaneme na niektorý z najľahších problémov. Napríklad na ten, či je na vrchu pyramídy faraón.

Otázka však je, koľko opakovaní bude tento postup potrebovať. Uvedomme si však nasledovné. Keďže \(m_2\) je najbližšia mocnina menšia ako \(p\), tak platí \(m_2 < p \leq 2m_2\). Nové poschodie, ktoré budeme musieť počítať je \(p-m_2\), čo s použitím predchádzajúcej nerovnice znamená, že od \(p\) sme odčítali aspoň jeho polovicu. V každom kroku sa nám teda číslo poschodia zmenší na aspoň polovicu.

Počet krokov bude teda najviac počet delení číslom 2, ktoré vieme s číslom \(p\) robiť, kým nedostaneme číslo 1. Toto číslo sa volá logaritmus a zapisujeme ho ako \(\log_2 p\). Táto hodnota navyše rastie veľmi pomaly. Ak by sme chceli napríklad vypočítať, či sa nachádza nejaký faraón v izbe \(147\) na poschodí \(10^9\) (miliarda), potrebovali by sme najviac 30 výpočtov. A porovnajte si to s tým, že by ste museli vypisovať celú pyramídu s miliardou riadkov.

Popísaný postup by sme mohli zapísať aj nasledovne. Za // sa nachádzajú komentáre pre lepšiu čitateľnosť.

najdi_faraona (p , c):    // zadáme poschodie (p) a izbu (c)
    opakuj až kým nie je koniec:
        ak p = 1 -> koniec, v tejto izbe je faraón    // poschodie 1 je jednoduché
        // vypočítame hodnotu m2
        m2 = 1
        opakuj kým m2 < p:
            m2 = m2 * 2
        m2 = m2 / 2    // keď skončí cyklus, v m2 je mocnina 2 väčšia alebo rovná p

        ak 2*m2 = p -> koniec, v tejto izbe je faraón    // p je mocnina 2
        v opačnom prípade ->
            ak p-m2 < c < m2+1 -> koniec, v tejto izbe faraón nie je    // prázdny priestor
            inak ak c <= p-m2 ->    // sme v ľavej menšej pyramíde
                p = p-m2
                c = c
            inak ->    // sme v pravej menšej pyramíde
                p = p-m2
                c = c-m2
        pokračuj v cykle s novými hodnotami p a c

Veľmi podobne bude tiež vyzerať riešenie v Pythone. Od vás sme samozrejme program nechceli, môže však byť zaujímavé sa na to pozrieť.

def najdi_faraona(p, c):
    while True:
        if p == 1:
            return True
        m2 = 1
        while m2 < p:
            m2 = m2 * 2
        m2 = m2 / 2
        
        if 2*m2 == p:
            return True
        else:
            if p-m2 < c and c < m2+1:
                return False
            elif c <= p-m2:
                p = p-m2
                c = c
            else:
                p = p-m2
                c = c-m2

p = int(input())
c = int(input())
if najdi_faraona(p, c):
    print('V izbe {} na poschodi {} sa nachadza faraon'.format(p,c))
else:
    print('V izbe {} na poschodi {} sa nenachadza faraon'.format(c,p))