4. Pyramídy vzorové riešenie

Zadanie

Táto úloha sa dá nahradiť riešením sady variables_cpp na Liahni (betaliahen.ksp.sk) . Ak chceš, aby ti namiesto bodov za riešenie tejto úlohy boli započítané body získané riešením spomínanej sady, na stránke odovdzaj pdf-ko s prezývkou, ktorú používaš na Liahni.

Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Baške na

Malý Miško dostal na narodeniny úplne novú sadu drevených kociek. Jeho obľúbenou stavbou je pyramída¹. Na obrázku nižšie si môžete pozrieť ako vyzerá pyramída s piatimi a so štyrmi poschodiami.

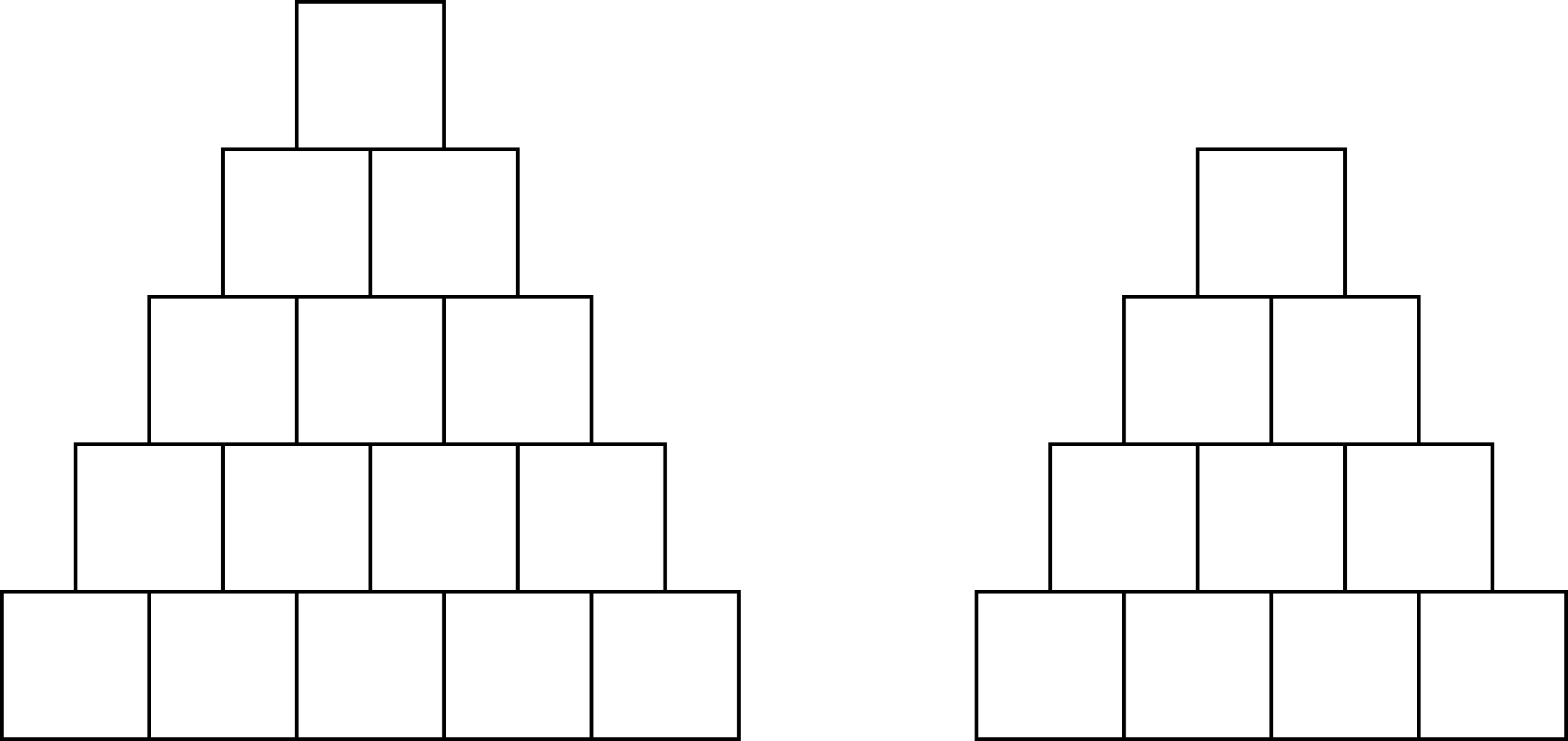
Spodný riadok \(k\)-poschodovej pyramídy sa skladá z \(k\) kociek. Každé ďalšie poschodie má o jednu kocku menej ako to pod ním. Takže počet kociek v pyramíde vieme vypočítať ako súčet čísel od 1 (najvrchnejšie poschodie) po \(k\) (najspodnejšie poschodie).

V matematickej knižke svojho otca dokonca Miško zistil, že tento súčet sa dá vyrátať aj pomocou jednoduchého vzorca:

\[1 + 2 + \ldots + k = \frac{k\cdot(k+1)}{2}\]

Aby urobil rodičom radosť, chcel by Miško postaviť jednu pyramídu pre maminku a jednu pre otecka. Zaujíma ho preto, či vie postaviť práve dve pyramídy a pritom použiť všetky kocky, ktoré má.

A keďže ho rodičia ešte nenaučili programovať², poprosil o pomoc vás.

Úloha

Na vstupe je číslo \(n\) – počet Miškových kociek.

Zistite, či vie postaviť dve (nie nutne rovnako vysoké) pyramídy, ktoré dokopy obsahujú práve \(n\) kociek. Samozrejme, pyramída, ktorá má 0 poschodí, sa za pyramídu nepovažuje.

Vstup

Vstup obsahuje jediný riadok s kladným celým číslom \(n\).

V sadách 4 a 5 bude číslo \(n\) naozaj veľké a nezmestí sa vám do štandardných 32 bitových premenných. Namiesto nich môžete použiť 64 bitové premenné (long long v C++, Int64 v Pascale). Takto veľké premenné odporúčame používať aj na ukladanie medzivýsledkov a pomocných premenných. V prípade, že používate Python tento problém nenastane, pretože premenné v Pythone môžu byť ľubovoľne veľké.

Výstup

Ak sa zo všetkých Miškových kociek dajú postaviť dve pyramídy, vypíšte slovo "ANO". V opačnom prípade vypíšte slovo "NIE".

Odpoveď vypisujte bez úvodzoviek okolo slov, všetko veľkými písmenami a nezabudnite vypísať koniec riadku!

Hodnotenie

Váš program bude spustený na piatich sadách vstupných súborov. Body dostanete za každú úspešne vyriešenú sadu. Obmedzenia na veľkosť čísla \(n\) v jednotlivých sadách nájdete v nasledujúcej tabuľke.

Číslo sady	1	2	3	4	5
maximálne \(n\)	\(100\)	\(10\,000\)	\(1\,000\,000\)	\(10^{10}\)	\(10^{12}\)

Príklady

Input:

256

Output:

ANO

Miško môže postaviť 2-poschodovú pyramídu z 3 kociek a 22-poschodovú pyramídu z \(\frac{22\cdot 23}{2} = 253\) kociek.

Input:

512

Output:

NIE

Z 512 kociek sa mu nepodarí postaviť dve kompletné pyramídy.

---

1. Miško zastáva názor, že obyčajné veže sú príliš nestabilné a môžu sa ľahko zrútiť.↩

2. Ale už čoskoro…↩

Spôsobov ako riešiť túto úlohu je mnoho. V tomto vzorovom riešení sa postupne pozrieme na niekoľko z nich, začínajúc od najmenej efektívnych.

Skúšame všetky možnosti

Ako prvé asi každému napadlo vyskúšať všetky možnosti. Postupne budeme skúšať výšku prvej pyramídy (túto výšku si označíme \(a\)) od 1 až po \(n\), druhej pyramídy (túto výšku si označíme \(b)\) tiež od 1 po \(n\). Pre každú dvojicu \(a,b\) si vieme vypočítať koľko kociek na tieto dve pyramídy potrebujeme: \[\frac{a\cdot(a+1)}{2} + \frac{b\cdot(b+1)}{2}\] Ak je tento súčet rovný \(n\), tak sme našli riešenie a môžeme skončiť.

Takéto riešenie by malo časovú zložitosť \(O(n^2)\), čo stačí na vyriešenie prvej sady¹. Môžeme si však všimnúť, že skúšame veľa zbytočných výšok. Pyramída s výškou \(n\) bude mať určite viac ako \(n\) kociek (pre \(n\) väčšie ako 1). Pokúsme sa teda určiť hornú hranicu pre \(a\) a \(b\) tesnejšie.

Otázka je, aké najväčšie môže byť \(a\), aby platilo, že počet kociek pyramídy výšky \(a\) je menší alebo rovný \(n\). Matematicky zapísané: \[\frac{a\cdot(a+1)}{2} \leq n\]

Jedna možnosť je vyjadriť si z toho hodnotu \(a\), čo naozaj spravíme na konci našeho vzorového riešenia. Ak sme ale lenivý, alebo nevieme ako sa riešia kvadratické rovnice, môžeme si pomôcť počítačom. Vhod nám príde cyklus while, ktorý beží tak dlho, kým platí nejaká podmienka. V našom prípade teda horeuvedená nerovnica.

#include <iostream>

using namespace std;

int main() {
    long long n;
    cin>>n;
    bool nasla = false;
    int a = 1;
    while (a*(a+1)/2 < n) {
        int b = 1;
        while (b*(b+1)/2 < n) {
            if (a*(a+1)/2 + b*(b+1)/2 == n) {
                nasla = true;
                break;
            }
            b++;
        }
        if (nasla) break;
        a++;
    }
    if (nasla) cout<<"ANO"<<endl;
    else cout<<"NIE"<<endl;
    return 0;
}

Časová zložitosť našeho riešenia závisí od toho, koľkokrát sa zopakujú naše dva while cykly. Označme si najväčšie číslo, pre ktoré platí nerovnica \[\frac{a\cdot(a+1)}{2} \leq n\] premennou \(max_a\). Časová zložitosť bude potom \(O(max_a^2)\). My by sme to však chceli vyjadriť pomocou premennej \(n\). Ako si ukážeme neskôr, hodnota \(max_a\) je zhruba \(\sqrt{n}\) a preto je zložitosť našeho riešenia \(O(n)\).

Predpočítanie veľkostí pyramíd

V predošlom riešení, sme si vždy znovu a znovu počítali veľkosť pyramídy s výškou \(a\). Skúsme si teda tieto hodnoty vypočítať vopred.

Využitím while cyklu, si vieme zistiť maximálnu hodnotu \(a\) – hodnota \(max_a\). Následne si vytvoríme pole takejto veľkosti. Použijeme vector, ktorý sa správa takmer ako polia ktoré poznáte. Na začiatku mu ale vieme v zátvorke povedať, akú má mať veľkosť². Následne sme do jeho jednotlivých políčok vypočítali príslušné hodnoty. V poli pyramidy teda máme všetky prípustné veľkosti pyramíd. Presnejšie, hodnota pyramidy[i] označuje, koľko kociek potrebujeme na postavenie pyramídy výšky \(i\).

Rovnako ako v predchádzajúcom riešení by sme mohli vyskúšať všetky dvojice veľkostí pre hodnoty \(a\) a \(b\) a overiť, či sa pyramidy[a]+pyramidy[b] rovná \(n\). To by však naše riešenie neurýchlilo. Ukážeme si preto dva rýchlejšie prístupy využívajúce toto pole.

Dvaja bežci

Vezmime si prípad, keď máme na vstupe číslo \(n=1194\), ktoré vieme dostať ako \(66 + 1128\). Pre takéto \(n\) bude hodnota \(max_a=49\), takže posledná hodnota v poli pyramidy bude číslo \(1225\). Pozrime sa teraz na súčet najmenšieho a najväčšieho čísla, teda \(1 + 1225\). Vidíme, že tento súčet je priveľký. Z toho ale vyplýva, že na číslo \(1225\) sa už nikdy nemusíme pozerať, pretože aj súčet s najmenším možným číslom je príliš veľký. Predposledné číslo v našom poli je číslo \(1176\). Ale \(1 + 1176 < 1194\), teda tento súčet je primalý. To ale znamená, že vo výsledku sa nemôže nachádzať ani \(1\), pretože ani jej súčet s najväčším prípustným číslom nie je dosť veľký. Preto sa posunieme na ďalšie číslo v poradí, teda číslo 3, s ktorým spravíme to isté. Opäť zistíme, že \(3+1176\) je príliš malé a 3 sa vo výsledku nachádzať nebude.

Zhrňmne si to. Budeme mať ukazovatele do našeho poľa – takzvaných bežcov. Prvý z nich bude začínať na najmenších číslach a bude sa celý čas posúvať v poli doprava (k väčším číslam), druhý začne na najväčších číslach a bude sa celý čas posúvať doľava (k menším číslam). Vždy, keď bude súčet veľkostí oboch bežcov menší ako \(n\), posunieme prvého bežca o jedno doprava, aby sme súčet zväčšili, a keď bude súčet väčší ako \(n\), posunieme druhého bežca o jedno doľava. Ak sa bude súčet čísel, na ktoré bežci ukazujú rovnať \(n\), tak sa môžeme zastaviť, pretože sme našli riešenie.

#include <iostream>
#include <vector>

using namespace std;

int main() {
    long long n;
    cin>>n;

    long long maxa = 1;
    while (maxa*(maxa+1)/2 < n) maxa++;
    vector<long long> pyramidy(maxa);
    for (long long i = 0; i<maxa; ++i) {
        pyramidy[i] = i*(i+1)/2;
    }

    int zlava = 1;
    int zprava = maxa-1;
    bool nasla = false;
    while(zlava <= zprava) {
        long long sucet = pyramidy[zlava] + pyramidy[zprava];
        if (sucet < n) {
            zlava++;
        } else if (sucet > n) {
            zprava--;
        } else {
            nasla = true;
            break;
        }
    }

    if (nasla) cout<<"ANO"<<endl;
    else cout<<"NIE"<<endl;
    return 0;
}

Ostáva nám odhadnúť časovú zložitosť. V riešení máme jeden while cyklus, ktorý vždy buď zväčší premennú zlava, zmenší premennú zprava, alebo ukončí program. Vezmime si prípad, že odpoveď je "NIE", takže while cyklus skončí na podmienke zlava <= zprava. V konečnom dôsledku sme premennú zlava zväčšili \(k\) krát, pre nejaké (možno nulové) \(k\). Rovnako sme premennú zprava zmenšili \(l\) krát pre nejaké (možno nulové) \(l\). Platí teda, že \(1 + k = (max_a - 1) - l\), takže \(k + l = max_a - 2\). Takže náš while cyklus sa vykoná najviac \(max_a - 2\) krát, z čoho vyplynie časová zložitosť \(O(max_a)\), teda \(O(\sqrt{n})\).

Binárne vyhľadávanie

Teraz sa na to pozrime inak. Máme na vstupe číslo \(1194\) a budeme postupne prechádzať poľom a každé z čísel skúsime ako veľkosť prvej pyramídy. Napríklad, máme číslo \(66\). Vieme teda, že veľkosť druhej pyramídy musí byť \(1194-66=1128\). Ak to naozaj je veľkosť nejakej pyramídy, tak sa musí nachádzať v poli pyramidy. Ako zistíme či sa číslo \(1128\) nachádza v poli pyramidy?

Určite poznáte hru “Mysli si číslo!”. Ja si myslím číslo do \(1024\), a vy tipujete aké číslo to je. Vždy keď si tipnete číslo, tak ja vám poviem “viac”, “menej” alebo “správne”. Najlepšou stratégiou je povedať ako prvé číslo 512. Podľa odpovede totiž viete zistiť, v ktorej polovici čísel sa nachádza hľadané číslo. Buď poviem “viac” a moje číslo je potom v intervale \(513-1\,024\), alebo poviem “menej” a ostane vám interval \(1-511\) (alebo ste ho trafili). V oboch prípadoch sa vám však interval možností zmenší na polovicu. No a na intervale polovičnej veľkosti viete spraviť to isté. Znova tipnete číslo uprostred tohto inetrvalu, a podľa odpovede zmenšíte jeho veľkosť na polovicu.

Rovnaký prístup môžeme použiť, ak hľadáme číslo v usporiadanom poli. Ako konce intervalu si budeme pamätať indexy do poľa. Na začiatku bude ľavý koniec zac na prvom prvku poľa, a pravý kon za koncom poľa (ukazuje na index poľa kde už nie je žiaden prvok). Stred poľa určíme ako stred = (kon+zac)/2. Pozrieme sa na stredný prvok, a ak je menší ako číslo ktoré hľadáme, tak posunieme zac na stred. Ak je väčší, tak posunieme kon na stred. Skončíme, v momente, keď platí kon = zac + 1. Potom zac ukazuje na hľadaný prvok (ak sa tam nachádza), a kon ukazuje hneď na prvok vpravo od neho.

Tento algoritmus sa volá binárne vyhľadávanie. Jeho časová zložitosť na \(k\) prvkoch je \(O(\log{k})\).

Keď už teda vieme v poli binárne vyhľadávať, tak si môžme jednoducho prejsť celé pole a k číslu pyramidy[i] skúsiť v poli nájsť číslo n-pyramidy[i].

#include <iostream>
#include <vector>

using namespace std;

int main() {
    long long n;
    cin>>n;

    long long maxa = 1;
    while (maxa*(maxa+1)/2 < n) maxa++;
    vector<long long> pyramidy(maxa);
    for (long long i = 0; i<maxa; ++i) {
        pyramidy[i] = i*(i+1)/2;
    }

    bool nasla = false;
    for (int i = 1; i<maxa; ++i) {
        long long hladame = n - pyramidy[i];
        int zac = 1, kon = maxa;
        while (kon-zac > 1) {
            int stred = (kon+zac)/2;
            if (pyramidy[stred] <= hladame) zac = stred;
            else kon = stred;
        }
        if(pyramidy[zac] == hladame) {
            nasla = true;
            break;
        }
    }

    if (nasla) cout<<"ANO"<<endl;
    else cout<<"NIE"<<endl;
    return 0;
}

Predpočítanie hodnôt nám trvá \(O(max_a)\), a potom máme jeden for-cyklus, počas ktorého robíme binárne vyhľadávanie. Samotný for-cyklus sa vykoná \(max_a\) krát, takže aj binárne vyhľadávanie spravíme \(max_a\) krát. Časová zložitosť bude teda \(O(max_a\cdot\log(max_a))\), čo je teda \(O(\sqrt{n} \cdot \log{\sqrt{n}})\).

Dopočítanie hodnoty b

Využime niečo z predošlého prístupu. Na vstupe máme \(1194\) a veľkosť prvej pyramídy \(66\), a chceme zistiť či \(1128 = 1194-66\) je tiež platná veľkosť pyramídy. Nedá sa to zistiť nejak jednoduchšie ako binárnym vyhľadávaním? No na to, aby toto číslo bolo veľkosťou nejakej pyramídy musí existovať celé číslo \(b\), pre ktoré platí \[1128 = \frac{b\cdot(b+1)}{2}\]

Takže stačí si vyjadriť \(b\). Číslo \(1128\) si označíme ako \(zv\) (veľkosť druhej pyramídy). \[zv = \frac{b\cdot(b+1)}{2}\] \[2zv = b\cdot(b+1)\] \[0 = b^2 + b - 2zv\]

Posledný výraz sa volá kvadratická rovnica. Táto rovnica môže mať až dva rôzne riešenia, ktoré si vieme vyjadriť vzrocom: \[D = \sqrt{1 - 4(-2zv)} = \sqrt{1 + 8zv}\] \[b_{1,2} = \frac{-1 \pm D}{2}\]

Našou úlohou je teraz nájsť kladné celé číslo \(b\), ktoré spĺňa túto rovnicu. Ak sa nám ho podarí nájsť, tak vieme, že zo \(zv\) kociek vieme poskladať pyramídu. Preto musí byť odmocnina z \(1+8zv\) celé číslo. Ak je, tak môžeme \(D\) dosadiť do druhého vzorca. Z tohto vzorca ľahko vidno, že v našom prípade bude jedno z možných riešení vždy záporné. Toto riešenie nás nezaujíma. Preto stačí \(D\) dosadiť iba do \(b = \frac{D - 1}{2}\). Po dosadení skontrolujeme, že sme dostali kladné číslo. Okrem toho aj skotrolujeme, či je \(D-1\) párne číslo³. Ak všetko platí, tak sme našli naše riešenie :D

#include <iostream>
#include <cmath>

using namespace std;

int main() {
    long long n;
    cin>>n;

    bool nasla = false;
    long long a = 1;
    while (a*(a+1)/2 < n) {
        long long c = a*(a+1) - 2*n;
        long long D2 = 1 - 4*c;
        if (D2 >= 0) {
            long long D = round(sqrt(D2));
            if (D*D == D2) {
                if ((D-1)%2 == 0) {
                    long long b1 = (-1 + D) / 2;
                    if (b1 > 0) {
                        nasla = true;
                        break;
                    }
                }
            }
        }
        a++;
    }
    if (nasla) cout<<"ANO"<<endl;
    else cout<<"NIE"<<endl;
    return 0;
}

V riešení používame iba jeden while cyklus, ktorý, ako už vieme, bude trvať \(O(max_a)\), teda \(O(\sqrt{n})\).

Prečo je \(O(max_a) = O(\sqrt{n})\)?

Vieme že pre \(max_a\) musí platiť rovnosť: \[\frac{max_a\cdot(max_a+1)}{2} = n\] \[max_a\cdot(max_a+1) = 2n\]

Ak by sme zanedbali tú plus jednotku, hodnotu \(max_a\) by sme odhadli ako odmocnicu z \(2n\). Čo pri použití \(O\)-notácie znamená, že: \(O(max_a) = O(\sqrt{2n}) = O(\sqrt{n})\).

Samozrejme, hodnotu \(max_a\) vieme vyjadriť aj exaktnejšie. Máme kvadratickú rovnicu \(max_a^2 + max_a - 2n = 0\) a jej kladné riešenie je \[max_a = \frac{-1 + \sqrt{1+8n}}{2}\]

Pri \(O\)-notácii, ktorú používame na zapisovanie časovej zložitosti však aj tak väčšinu konštánt zanedbávame a preto prídeme k rovnakému výsledku, že \(O(max_a) = O(\sqrt{n})\).