2. Pestovanie ovocia v Absurdistane vzorové riešenie

V tomto vzorovom riešení postupne vyriešime jednotlivé podúlohy a pri každej skúsime načrtnúť aj postup, ktorým sme mohli dospieť k správnemu riešeniu.

a) \(1, 2, 3, 1, 2, 3, 1, \dots\)

V prvom roku máme mať jednu rastlinu. Tu nemáme príliš nad čím rozmýšľať – pomenujeme ju A a zasadíme ako prvú. Takisto vieme, že v druhom roku máme mať dva plody. Tie nutne musí urodiť A, preto jej zatiaľ dáme predpis A \(\rightarrow\) BC. Z týchto dvoch sa nám majú urodiť 3 plody. Tie sa kľudne môžu urodiť z jednej z nich, a druhú necháme bez plodov: C \(\rightarrow\) 0.

Vieme, že v treťom roku musí vyrásť rastlina, na ktorej sa opäť urodí A, aby sa celý tento cyklus mohol opakovať. Túto rastlinu nazveme D a bude mať predpis D\(\rightarrow\)A. Rastlina D sa musí urodiť na rastline B a zvyšné dve rastliny, ktoré sa na B urodia by mali na ďalší rok zahynúť, aby nám ostala iba rastlina A. No a vymierajúcu rastlinu už máme v podobe C. Preto posledné pravidlo bude B\(\rightarrow\)DCC.

Rastliny, ktoré budeme postupne dostávať, sú A, BC, DCC, A … Toto riešenie je navyše správne, lebo prvé štyri roky tvoria postupnosť \((1, 2, 3, 1)\) a v štvrtom roku máme rovnakú rastlinu A ako v prvom roku. Nutne sa teda táto postupnosť bude opakovať.

b) \(x, +2, -1, +2, -1, +2, \dots\)

Striedavo nám v jednom roku pribúdajú dve rastliny, a jedna ubúda. Ubúdanie rastliny vyriešime rastlinou C\(\rightarrow\)0 z minulej podúlohy. Chceme aby nám každý druhý rok vyrástla jedna takáto rastlina. Zároveň potrebujeme nejakú rastlinu A, z ktorej v predchádzajúci rok vyrastú tri rastliny (aby sme mali dokopy +2 rastlín). Jedna z týchto rastlín bude C, ktorá nám zabezpečí žiadaný pokles o jeden na ďalší rok. Máme teda A\(\rightarrow\)BCD a C\(\rightarrow\)0. Zvyšné dve rastliny BC musia dokopy urodiť dva plody – ak by urodili menej alebo viac, nemali by sme celkový zisk -1, ktorý nám už zabezpečuje C. Takisto vieme, že v nasledovnom roku budeme chcieť vypestovať rastlinu A, aby sme tento proces začali odznova. Dajme si teda B\(\rightarrow\)A. A sme pritom navrhli tak, aby samo o sebe spustilo proces +2, -1 v ďalších rokoch. To znamená že zostávajúca rastlina D by už nikdy nemala mať dopad na počet plodov – mala by sa len zachovávať. Predpíšeme teda D\(\rightarrow\)D.

Celé riešenie je teda A\(\rightarrow\)BCD, B\(\rightarrow\)A, C\(\rightarrow\)0 a D\(\rightarrow\)D. V každom druhom roku budeme v rovnakej situácií ako na začiatku, len budeme mať zakaždým o jednu trvanlivú rastlinu D naviac. Jediná rastlina A v takomto roku potom spôsobí žiadané zmeny +2, -1 v nasledujúcich rokoch, a tento proces sa bude opakovať.

c) \(x, *4, /2, *4, /2, \dots\)

Čím ďalej, tým častejšie vytvárame rastliny na plnenie špecifických úloh. Odteraz si teda budeme rastliny aj pomenovávať v závislosti od funkcie, ktorú budú plniť.

Prvou takou rastlinou bude rastlina ‘násobič’ A. Presný predpis tejto rastliny dopredu nevieme, chceme však rastlinu ktorá sa do budúceho roku rozmnoží na štyri. Jednu takúto rastlinu zasadíme v prvom roku a tá sa nám rozmnoží na štyri, zatiaľ neurčené, rastliny. Aké rastliny by boli vhodné? No z týchto štyroch rastlín ktoré vyrastú v druhom roku, chceme mať len dva plody, aby sme do tretieho roku mali žiadanú zmenu počtu \(/2\).

Zároveň, rovnako ako v minulej podúlohe, sa nám tento proces začne odznova – následne budeme chcieť počet rastlín zoštvornásobiť. Na to sme už vytvorili násobiča A, teda v tomto roku budeme chcieť aby obe vyrastené rastliny boli A. Zatiaľ teda vieme, že počas prvých rokov by mala situácia vyzerať A\(\rightarrow\)????\(\rightarrow\)AA. Aspoň z dvoch ? nám do ďalšieho roka nesmie nič narásť – potrebujeme akúsi rastlinu ‘samovrah’. Takú však máme z predchádzajúcej podúlohy. Je ňou rastlina C\(\rightarrow\)0.

Teda A\(\rightarrow\)??CC\(\rightarrow\)AA. Teraz už vidíme jednoduché riešenie – obe zostávajúce ? budú rastlina ‘spáč’ B\(\rightarrow\)A, ktorej úloha je jeden rok prespať a v ďalšom roku sa zmeniť na násobiča A.

Celkovo teda dostávame A\(\rightarrow\)BBCC\(\rightarrow\)AA. V treťom roku máme rovnaké rastliny ako v prvom, akurát ich je dvojnásobne viac. Ďalšie dve roky teda budú opäť vyzerať rovnako – dostaneme zmenu \(*4\) a potom \(/2\), pričom sa nám počet rastlín A opäť zdvojnásobí.

d) \(x,*2, +1, *2, +1, *2, \dots\)

Táto podúloha sčasti kombinuje dve predošlé podúlohy – v jeden rok chceme počet rastlín násobiť, a hneď nato zmeniť o konštantú hodnotu.

Na začiatok sa pokúsme vyriešiť úlohy, kde by zadaná postupnosť vyzerala \((x, *2, +0, *2, +0 \dots)\). Teda počet rastlín sa nám každý druhý rok zdvojnásobí. Zdvojnásobenie je ľahké, stačí použiť rastlinu C\(\rightarrow\)CC. Avšak takéto rastliný sa budú násobiť každý rok. Tak ako v predchádzajúcej podúlohe si však môžeme pridať rastlinu ‘spáč’, ktorá zaručí, že v nasledujúci rok sa nič nezmení, teda naozaj bude prírastok \(+0\).

Rastliny teda môžu vyzerať nasledovne: C\(\rightarrow\)DD a D\(\rightarrow\)C. C teda vytvorí dvoch spáčov D, ktorý sa nasledujúci rok iba prepíšu na ‘násobiča’ C, čím nespôsobia zmenu v párne roky, ale zaručia, že v nepárny rok sa počet rastlín opäť zdvojnásobí. Rastlina D teda slúži len na zdržanie našeho násobenia.

Do vzorového riešenia však musíme pridať aj to, aby sa každý párny rok pridal jeden nový plod. Keďže je len jeden, stačí si na to vyhradiť jednu rastlinu. Táto rastlina však musí vedieť, či je rok párny alebo nepárny. Ale tak ako predtým, toto vieme ľahko vyriešiť pomocou striedania dvoch rastlín. Presnejšia, keby sme mali A\(\rightarrow\)B a B\(\rightarrow\)A, pričom začíname s rastlinou A, tak vieme, že vždy keď sadíme A je rok nepárny a keď B tak rok párny.

Ostáva už len domyslieť, čo pridať na pravú stranu oboch týchto šipiek. Keď sadíme rastlinu B, potrebujeme aby nám vyrátlo o jednu rastlinu viac. To znamená, že okrem zadaného A musí vyrásť aj nejaká iná rastlina ?. Táto rastlina sa potom v ďalšom roku musí zdvojnásobiť. A na to predsa slúži rastlina C a teda B\(\rightarrow\)AC.

No a keď máme rastlinu A, tak počet rastlín sa musí v daný rok zdvojnásobiť. To znamená, že A musí okrem B vytvoriť ešte jednu rastlinu ?. No a táto rastlina má v ďalšom roku iba nahradiť samú seba, keďže o \(+1\) sa postará B, a potom sa začať každý druhý rok zdvojnásobovať. A takto predsa funguje rastlina D.

Finálne riešenie je teda A\(\rightarrow\)BD, B\(\rightarrow\)AC, C\(\rightarrow\)DD a D\(\rightarrow\)C, pričom nám stačí ako prvú zasadiť rastlinu A.

Aby sme ukázali, že toto riešenie je správne, môžeme ukázať, že v nepárne roky sadíme iba rastliny A a C, ktoré sa v daný rok naozaj zdvojnásobia a v nepárne roky sadíme iba rastliny B a D, ktoré nahrádzajú samé seba. S výnimkou, že B vytvorí ešte jednu rastlinu naviac, aby sme získali \(+1\), ale to je dobre, lebo máme práve jednu rastlinu B.

e) \(n\)-té Fibonacciho číslo

Pripomeňme si najskôr, ako počítame Fibonacciho čísla. Označme si \(n\)-té Fibonacciho číslo ako \(F_n\). Vieme, že \(F_0=1\) a \(F_1=1\). No a na základe týchto dvoch hodnôt už vieme vypočítať všetky väčšie, keďže \(n\)-té Fibonacciho číslo dostaneme ako súčet predchádzajúcich dvoch, teda \(F_n = F_{n-1} + F_{n-2}\).

Pokúsme sa využiť túto vlastnosť. Predstavme si, že sa nám podarilo mať v \(n\)-tom roku vypestovaných \(F_n\) rastlín. Tieto rastliny si vieme rozdeliť na dve kôpky – jednu veľkosti \(F_{n-1}\) a druhú veľkosti \(F_{n-2}\). Nech všetky rastliny v prvej kôpke sú rastliny A a všetky rastliny v druhej kôpke rastliny B. Tieto rastliny následne zasadíme.

Čo musí platiť, aby sa nám z nich urodilo dokopy \(F_{n+1}\) rastlín? Vieme, že \(F_{n+1} = F_n + F_{n-1}\), teda sa nám má urodiť \(F_n\) rastlín A a \(F_{n-1}\) rastlín B. Vidíme, že ak by sa z každej rastliny A, ktorých máme zatiaľ iba \(F_{n-1}\) urodila jedna rastlina B, tak v ďalšom roku budeme mať naozaj \(F_{n-1}\) rastlín B. No a aby sa nám urodilo \(F_n\) rastlín A, musí z každej zasadenej rastliny vyrásť rastlina A.

Táto myšlienka nás vedie k dvom veľmi jednoduchým pravidlám: A\(\rightarrow\)AB a B\(\rightarrow\)A, pričom začínať budeme s jednou rastlinou A. Postupnosť rastu teda bude A\(\rightarrow\)AB\(\rightarrow\)AAB\(\rightarrow\)AAABB…

Zopakujme si teda ešte raz, čo presne robí naše riešenie. Po \(n\)-tom roku máme vypestovaných \(F_n\) rastlín. Z toho presne \(F_{n-1}\) je rastlín A a presne \(F_{n-2}\) je rastlín B, čo teda v súčte naozaj dáva hodnotu \(F_n\). Keď tieto rastliny zasadíme, tak z každej rastliny vyrastie jedna rastlina A, teda budeme mať \(F_n\) rastlín A a z každej rastliny A vyrastie rastlina B, takže budeme mať \(F_{n-1}\) rastlín B. Dokopy budeme mať \(F_n + F_{n-1} = F_{n+1}\) rastlín, čo je presne počet čo sme chceli. Naviac, opäť bude platiť, že počet A-čok je predchádzajúce Fibonacciho číslo a počet B-čok to ešte pred tým. Túto úvahu teda budeme môcť použiť znova a naše riešenie je korektné.

f) \(n^2\)

V tejto úlohe bola nápomocná vizualizácia – nie nadarmo sa číslo \(n^2\) nazýva štvorec čísla \(n\). Naše rastliny teda zasaďme do štvorca, ktorý má \(n\) riadkov a \(n\) stĺpcov. Začínať budeme s jednou rastlinou. No a aby sme zo štvorca \(n \times n\) dostali štvorec \((n+1) \times (n+1)\), potrebujeme k tomu menšiemu štvorcu pridať jeden riadok na spodok a jeden stĺpec napravo.

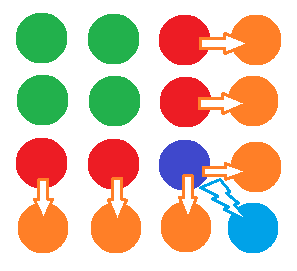
Na obrázku je znázornený prechod záhrady z tretieho do štvrtého roku. Oranžové a svetlomodrá rastlina sú tie, ktoré v tomto roku museli vyrásť, všetky ostatné sa museli zachovať. Ostáva z obrázku vyčítať, ako vyzerajú pravidlá pre jednotlivé rastliny.

Zelené rastliny (Z) nemuseli spraviť nič, stačilo, že sa zachovali aj do ďalšieho roka. Preto pridáme pravidlo Z\(\rightarrow\)Z. Zaujímavejšie je to však s rastlinami, ktoré boli na kraji štvorca \(3\times 3\). V ich blízkosti totiž museli pribudnúť nové rastliny. A dáva zmysel, aby sa práve červená rastlina postarala o to, že veľa nej niečo vyrastie.

Pozrime sa teda bližšie na červenú rastlinu (C). Nestačí, že sa táto rastlina zachová, musí spraviť aj o jednu rastlinu naviac, rastlinu, ktorá je na obrázku označená oranžovou. Teda potrebujeme pravidlo C\(\rightarrow\)??. Ostáva zistiť, čo dať na miesto otáznikov. Miesto, kde leží červená rastlina nebude v ďalšom roku na spodnom ani pravom kraji. To znamená, že od toho momentu sa toto miesto už len má nahrádzať samo sebou, čo úspešne robí rastlina Z. A čo má robiť novovzniknutá oranžová rastlina? Keďže bude v ďalšom roku na kraji, označili by sme ju červenou farbou, lebo presne tak by sa mala správať. Preto dostaneme pravidlo C\(\rightarrow\)ZC.

Trochu špeciálne sa bude správať modrá rastlina M. Tá má totiž až dvoch oranžových susedov a naviac sa musí postarať o tom, aby sme zaplnili novovzniknutý pravý dolný roh. A k tomu všetkému sa musí aj zachovať. Preto potrebujeme pravidlo M\(\rightarrow\)????. Je jasné, že obe nové oranžové rastliny sa v ďalšom roku musia chovať ako C a preto dva zo štyroch ? nahradíme týmto písmenom. Na mieste aktuálnej modrej rastliny sa ďalej už nič diať nebude, a teda tam patrí rastlina Z. No a posledný otáznik musíme nahradiť M. Pretože aj v ďalšom roku budeme potrebovať, aby sa niektorá rastlina postarala o pravý dolný roh.

Naše riešenie teda bude začínať s jednou rastlinou M a bude mať pravidlá M\(\rightarrow\)ZCCM, C\(\rightarrow\)ZC a Z\(\rightarrow\)Z.