Zadanie
Ak máte akékoľvek otázky ohľadom tejto úlohy napíšte Michalovi ‘Žabovi’ Anderlemu na [email protected]
Viete ako sa cestuje v Absurdistane? Tak ja vám to vysvetlím.
V Absurdistane je \(n\) miest, ktoré sú navzájom pospájané niekoľkými cestami. Každá cesta vedie medzi niektorými dvoma mestami a dá sa po nej pohybovať v oboch smeroch. Naviac sa žiadne dve cesty nekrižujú. Ak sa teda po niektorej z nich vyberiete, zísť z nej môžete iba v jednom z miest, ktoré spája. No, a našťastie, cestovať sa dá medzi ľubovoľnými dvoma mestami. Občas možno treba prejsť viacerými cestami, určite sa však viete dostať odvšadiaľ všade.
Problém je však v tom, že všetky cesty sú zastarané, neudržiavané a plné výmoľov. Vláda Absurdistanu sa preto rozhodla, že s tým treba niečo spraviť a niektoré cesty zrenovovať. Samozrejme, renovácia cesty niečo stojí a preto chce zrenovovať čo najmenej ciest. Zároveň však chce pôsobiť dojmom, že renovácia bola naozaj veľká. Chcela by preto zrenovovať také cesty, aby sa medzi každými dvoma mestami dalo cestovať iba po zrenovovaných cestách.
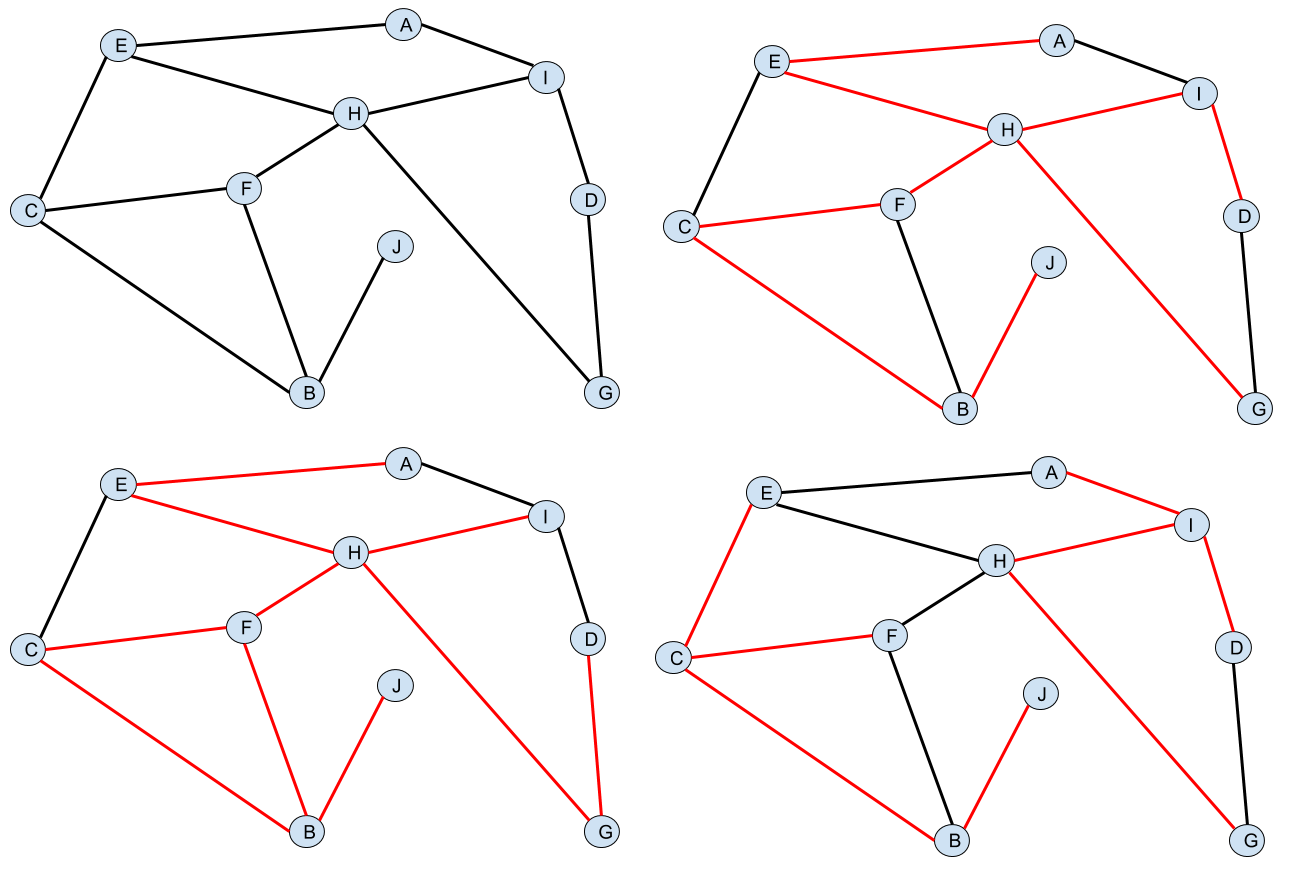
Na obrázku vľavo hore je príklad s desiatimi mestami, medzi ktorými vedie trinásť ciest. Napravo od neho sú červenou zvýraznené cesty, ktoré by mohla vláda Absurdistanu zrenovovať tak, aby zrenovovala čo najmenej ciest a zároveň sa dalo cestovať medzi každými dvoma cestami iba po zrenovovaných cestách. Táto možnosť samozrejme nie je jediná správna. Na nižších dvoch obrázkoch sú príklady rekonštrukcie, ktoré nespĺňajú niektorú požiadavku. Možnosť naľavo renovuje priveľa ciest (napríklad cestu medzi C a F nemusíme rekonštruovať), v možnosti napravo sa zase nevieme dostať po zrenovovaných cestách z mesta F do mesta A.
Úloha
(1 bod) Koľko najmenej ciest musí vláda Absurdistanu zrenovovať aby sa medzi každými dvoma mestami dalo cestovať iba po zrenovovaných cestách? Nezabudnite, že v Absurdistane je \(n\) miest, takže hľadaná odpoveď asi bude závisieť od tejto hodnoty.
(2 body) Popíšte postup (algoritmus), akým môže vláda Absurdistanu vybrať, ktoré cesty má zrekonštruovať.
Popísať postup (algoritmus) je napísať nejakú postupnosť krokov a pravidiel, ktoré jednoznačne určia, ktoré cesty má vláda Absurdistanu vybrať, pričom tento postup funguje bez ohľadu na to, ako vyzerá plán ciest Absurdistanu.
Ak si chcete vyskúšať, či je váš postup dobrý a zrozumiteľný, poproste o pomoc napríklad jedného z rodičov. Nakreslite mu plán Absurdistanu (napríklad ten z obrázku vyššie) a povedzte mu, aby riadiac sa vašim postupom, vybral cesty, ktoré sa majú zrenovovať.
(5 bodov) Vláda Absurdistanu však zistila, že niektoré cesty sú náročnejšie na renováciu. Presnejšie, o každej ceste vie povedať, či jej renovácia bude stáť 1 alebo 2 milióny dolárov. Stále chce zrekonštruovať cesty tak, aby sa medzi každými dvoma mestami dalo cestovať iba po zrekonštruovaných cestách, naviac však chce zaplatiť čo najmenej peňazí.
Popíšte postup, ktorým môže vláda Absurdistanu vybrať cesty, ktoré má zrekonštruovať. Naviac zdôvodnite, prečo je váš postup správny a nájde najlacnejšie riešenie za každých okolností.
Pri zdôvodňovaní sa skúste zamyslieť nad nasledovnými otázkami. Je treba vybrať viac ciest ako v riešení a)? Zmení sa úloha ak by sme namiesto hrán s hodnotami 1 a 2 mali hrany s hodnotami 0 a 1? Prečo sa mi neoplatí vybrať inú cestu?
(7 bodov) Hĺbková analýza terénu prišla s ešte horšími výsledkami. Zistilo sa, že renovácia rôznych ciest stojí rôzne množstvo peňazí. Za renováciu cesty môžeme občas zaplatiť 1 milión dolárov a občas až \(1\,000\,000\) miliónov dolárov. Našťastie, o každej ceste vieme, koľko bude stáť jej renovácia a takisto vieme, že všetky cesty majú tieto hodnoty rôzne.
Popíšte postup, ktorý pomôže vláde Absurdistanu vybrať také cesty, ktorých renovácia bude stáť najmenšie množstvo peňazí a stále bude platiť, že medzi ľubovoľnými dvoma mestami sa dá cestovať pomocou zrenovovaných ciest. Zdôvodnite, prečo je váš postup správny a nájde najlacnejšie riešenie za každých okolností.
Pri zdôvodňovaní sa skúste zamyslieť nad nasledovnými otázkami. Môže sa stať, že by najlacnejšie riešenie nebolo jednoznačné? Ak sa o nejakej ceste rozhodnem, že ju chcem zrenovovať, patrí táto cesta do najlacnejšieho riešenia? Čo by sa stalo, ak by najlacnejšie riešenie túto cestu nepoužívalo, ale my by sme ju doňho aj tak pridali?
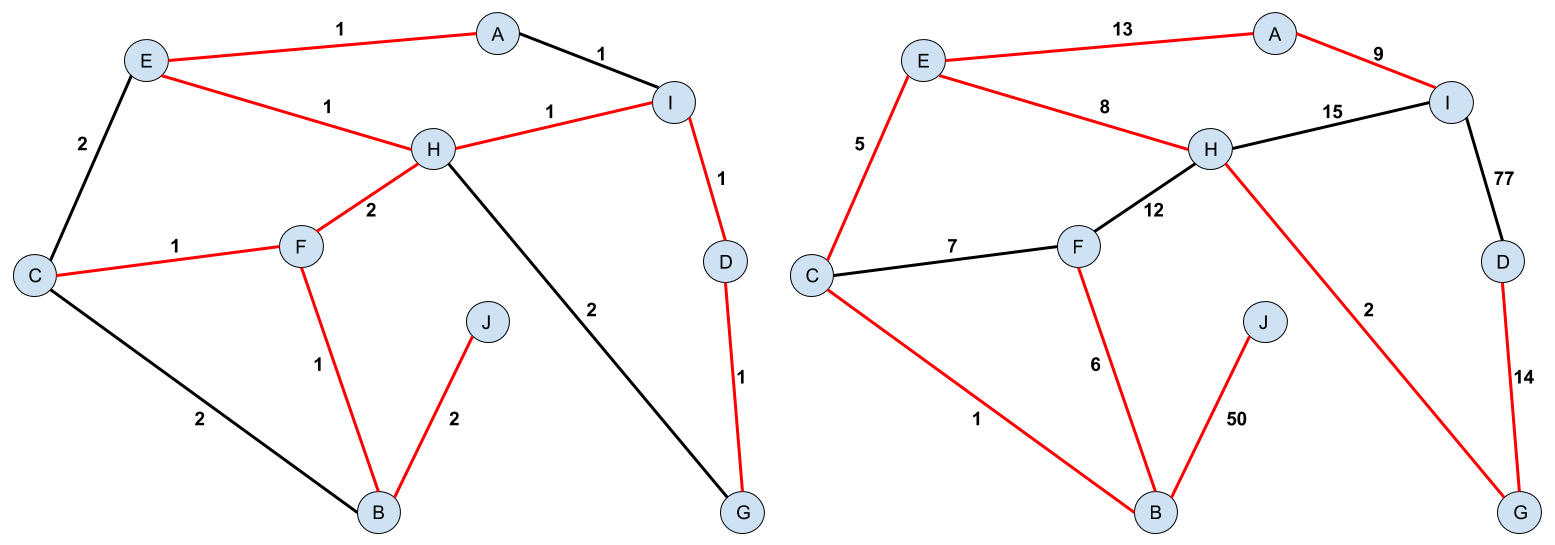
Na obrázku je príklad k podúlohe c) a d) aj s možným optimálnym riešením. Čísla pri cestách určujú cenu renovovania danej cesty. Cena prvého riešenia je 11 miliónov dolárov, druhého 108 miliónov dolárov.
Na začiatok si pripomeňme zadanie úlohy. Dostali sme mapu Absurdistanu, na ktorej bolo \(n\) miest, medzi ktorými viedli nejaké cesty. Našou úlohou bolo vybrať cesty, ktoré sa budú rekonštruovať. Cieľom bolo vybrať takýchto ciest čo najmenej, lebo rekonštrukcia je drahá, ale zároveň docieliť, aby sa medzi každými dvoma mestami dalo cestovať iba po zrenovovaných cestách.
Skôr ako sa pustíme do riešenia, musíme si zadefinovať pojem komponent, ktorý budeme počas tohto vzorového riešenia hojne používať. Komponentom nazývame skupinu miest, medzi ktorými sa dá pohybovať iba po zrekonštruovaných cestách.
Na obrázku nižšie si môžete pozrieť ako môže vyzerať Absurdistan. Červenou farbou sú označené zrekonštruované cesty. Na obrázku naľavo sú 3 komponenty – (A, E, H, I), (D, G) a (C, B, F, J). Na obrázku napravo sú komponenty až 4 – (A), (E, H, I, F, G), (D) a (C, B, J). Všimnite si, že aj osamotený vrchol tvorí komponent.
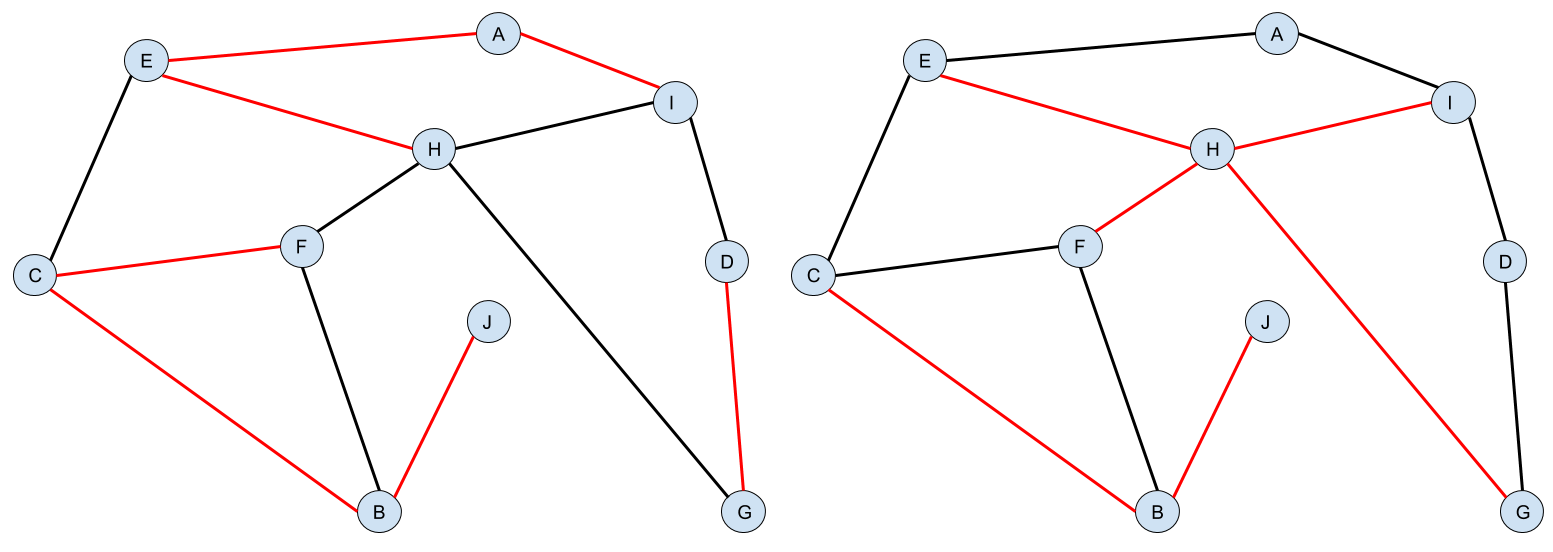
Ak sme ešte nezrekonštruovali žiadnu cestu, v Absurdistane sa nachádza \(n\) komponentov – každé mesto tvorí samostatný komponent odkiaľ sa nevieme pohnúť ďalej. No a našou úlohou je zrekonštruovať také cesty, aby bol v Absurdistane iba jeden komponent, ktorý obsahuje všetky mestá. Potom sa z definície dá dostať z každého mesta do každého iného iba po zrekonštruovaných cestách.
Podúlohy a) a b)
Ako však zistíme, ktoré cesty chceme vybrať? Skúsme ich postupne rekonštruovať, je úplne jedno v akom poradí. Aby sme však nezrenovovali všetky cesty, vždy pred renováciou si položíme dôležitú otázku: Pomôže nám rekonštrukcia tejto cesty?
Predstavme si, že uvažujeme o ceste, ktorá vedie medzi mestami X a Y. V úvahu pripadajú dve možnosti. Obe tieto mestá ležia v tom istom komponente, teda už sa medzi nimi dá pohybovať iba po zrekonštruovaných cestách. V takom prípade nám však rekonštrukcia cesty medzi X a Y v ničom nepomôže. Ak už existoval spôsob ako medzi týmito dvoma mestami prejsť iba po zrekonštruovaných cestách, vždy, keď by sme chceli použiť túto priamu cestu, môžeme to radšej obísť. A ušetríme si jednu rekonštrukciu.
Druhá možnosť nastane ak mestá X a Y neležia v tom istom komponente. V takom prípade nám rekonštrukcia tejto cesty pomôže, lebo odteraz sa budeme vedieť dostať z X do Y (a naopak). A nielen to. Ak mesto A bolo v tom istom komponente ako X a mesto B v tom istom komponente ako Y, tak zrazu sa vieme dostať aj z mesta A do mesta B a to iba po zrekonštruovaných cestách. Stačí ak najskôr pôjdeme z A do X (takýto spôsob existuje, lebo sú v tom istom komponente), potom prejdeme po novozrekonštruovanej ceste do Y a odtiaľ do mesta B (takýto spôsob existuje, lebo sú v tom istom komponente). Zrekonštruovanie tejto cesty nám teda spojilo príslušné dva komponenty a nahradilo ich jedným väčším.
A to je v konečnom dôsledku náš cieľ. Spojiť \(n\) samostatných komponentov do jedného veľkého. Takýto postup vieme aj veľmi jednoducho zapísať a pochopia ho aj vaši rodičia:
postupne pre každú cestu v Absurdistane sprav:
ak sa mestá na koncoch tejto cesty nachádzajú v rovnakom komponente
(dá sa medzi nimi dostať iba po zrekonštruovaných cestách), tak:
s touto cestou nič nerob
ak sa nenachádzajú v rovnakom komponente, tak:
zrekonštruuj túto cestuTento postup určite povedie k tomu, že nám ostane jeden veľký komponent a teda sa budeme vedieť dostať odvšadiaľ všade iba po zrekonštruovaných cestách. Vyberie však tento postup minimálny počet ciest? A koľko ich vlastne vyberie?
Spomeňme si, čo sa stane ak v tomto postupe zrekonštruujeme nejakú cestu – spojíme dva komponenty do jedného väčšieho. To znamená, že počet komponentov klesne o 1. No a ak sme začínali s \(n\) komponentami (každé mesto je samostatný komponent) a skončili sme s 1 komponentom, museli sme takéto spájanie spraviť presne \(n-1\) krát. Zrekonštruovali sme teda \(n-1\) ciest.
Toto je však aj dôvod, prečo je tento počet zrekonštruovaných ciest najmenší možný. Ľubovoľná rekonštrukcia niektorej cesty vie spojiť najviac dva komponenty. A preto musíme zrekonštruovať aspoň \(n-1\) ciest.
Podúloha c)
V podúlohe c) je situácia trochu komplikovanejšia. Za rekonštrukciu cesty totiž musíme zaplatiť, v tomto prípade 1 alebo 2 milióny dolárov. Našou úlohou je opäť zrekonštruovať také cesty, aby sa medzi každými dvoma mestami dalo pohybovať iba po zrekonštruovaných cestách, ale zároveň chceme zaplatiť čo najmenej peňazí.
Pri predchádzajúcej úlohe sme si ukázali, že musíme postaviť aspoň \(n-1\) ciest. Táto podmienka sa nezmení ani teraz. Ak by sme totiž postavili viac ciest, určite sa nájde taká, ktorej nezrekonštruovanie neporuší podmienku zo zadania. A ak ju nezrenovujeme, tak samozrejme ušetríme nejaké doláre.
Líši sa však táto úloha až tak veľmi od úlohy predchádzajúcej? Cesty predsa majú len dve možné ceny. Znie prirodzene, že ak chceme za rekonštrukciu zaplatiť čo najmenej peňazí, chceme zrekonštruovať čo najviac ciest s cenou 1. Najlepšie by dokonca bolo, ak by sme nemuseli zrekonštruovať žiadnu cestu s cenou 2.
Čo sa stane ak použijeme postup z podúlohy b), ale spustíme ho iba pre cesty s cenou 1? Medzi niektorými mestami sa bude dať prechádzať a získame tak niekoľko komponentov. V prípade, že nám ostane iba jeden komponent, tak algoritmus môžeme ukončiť, našli sme riešenie s cenou \(n-1\), čo je najmenšia cena, ktorú vieme získať. Čo však v prípade, že tých komponentov ostane viacero?
Uvedomme si, že žiadna cesta s cenou 1 nám už nepomôže. To že sme ju nezrekonštruovali znamená, že vedie medzi dvoma mestami, medzi ktorými sa vieme pohybovať len po zrekonštruovaných cestách. Zároveň sme však použili najväčší počet ciest s cenou 1, aké sme použiť mohli. Skúsili sme totiž každú jednu z nich a nezrekonštruovali sme iba tie, ktoré nám nespojili žiadne dva komponenty. Ostáva nám teda už len pospájať zvyšné komponenty pomocou ciest s cenou 2.
A to vieme spraviť úplne rovnako. Pre každú cestu s cenou 2 sa spýtame, či nám jej zrekonštruovanie pomôže, teda či jej koncové mestá ležia v tom istom komponente. Ak neležia, takúto cestu zrekonštruujeme, čím zmenšíme počet komponentov. Samozrejme, cesty s cenou 1, ktoré sme sa rozhodli zrekonštruovať, pokladáme pri cestách s cenou 2 za zrekonštruované.
postupne pre každú cestu s cenou 1 sprav:
ak sa mestá na koncoch tejto cesty nachádzajú v rovnakom komponente
(dá sa medzi nimi dostať iba po zrekonštruovaných cestách), tak:
s touto cestou nič nerob
ak sa nenachádzajú v rovnakom komponente, tak:
zrekonštruuj túto cestu
postupne pre každú cestu s cenou 2 sprav:
ak sa mestá na koncoch tejto cesty nachádzajú v rovnakom komponente
(dá sa medzi nimi dostať iba po zrekonštruovaných cestách), tak:
s touto cestou nič nerob
ak sa nenachádzajú v rovnakom komponente, tak:
zrekonštruuj túto cestuPodúloha d)
Vymyslieť správne riešenie tejto podúlohy, kde má každá cesta inú cenu, by malo byť pomerne jednoduché. Samozrejme, že chceme uprednostňovať lacnejšie cesty. A nechceme vybrať cestu, ktorá spája dve mestá, ktoré už sú v tom istom komponente. Môžeme preto použiť riešenie z podúlohy b), akurát nebudeme cesty spracovávať v ľubovoľnom poradí, ale od najlacnejšej po najdrahšiu. Aj toto je však veľmi ľahko zapísateľné.
usporiadaj všetky cesty od najlacnejšej po najdrahšiu
postupne pre každú cestu v usporiadanom poradí sprav:
ak sa mestá na koncoch tejto cesty nachádzajú v rovnakom komponente
(dá sa medzi nimi dostať iba po zrekonštruovaných cestách), tak:
s touto cestou nič nerob
ak sa nenachádzajú v rovnakom komponente, tak:
zrekonštruuj túto cestuToto riešenie je dokonca také isté ako riešenie v podúlohe c), aj tam totiž s cestami robíme zakaždým to isté, a spracovávame ich v utriedenom poradí. Najskôr všetky s cenou 1, potom všetky s cenou 2.
To, čo je ťažké na tejto podúlohe je dokázať, že takéto riešenie je správne a naozaj nájde najlacnejšie možné riešenie.
Predpokladajme, že naše riešenie je zlé. To znamená, že existuje iné, optimálne riešenie, v ktorom za zrekonštruovanie zaplatíme najmenšie množstvo dolárov. Vieme, že aj toto riešenie musí rekonštruovať \(n-1\) ciest, rovnako koľko zrekonštruuje aj naše riešenie1. Tieto dve riešenia sa však v niečom musia líšiť.
Predpokladajme, že optimálne riešenie zrekonštruuje cestu medzi mestami X a Y, ale naše riešenie túto cestu nezrekonštruuje. Prečo to nespraví? Jediný dôvod nezrekonštruovať túto cestu, má naš algoritmus v prípade, ak v okamihu keď sa rozhoduje o zrekonštruovaní tejto cesty, patria mestá X a Y do rovnakého komponentu. To ale znamená, že v Absurdistane existuje medzi mestami X a Y taká trasa, ktorá vedie iba po cestách lacnejších ako cesta z X do Y.
Odkiaľ sme toto zistili? Cesty predsa spracovávame v usporiadanom poradí od najlacnejších. Takže ak sa v našom riešení mestá X a Y nachádzali v tom istom komponente (a preto sme nezrekonštruovali cestu medzi X a Y), tak medzi týmito mestami sa dalo dostať iba po zrekonštruovaných, a teda lacnejších cestách.
Čo to znamená, pre naše optimálne riešenie? Odstráňme z neho cestu medzi X a Y. V takomto riešení sa teraz medzi týmito dvoma mestami nedá dostať. Musíme teda pridať nejakú cestu, ktorou to opravíme. Zoberme si iba cesty z trasy medzi X a Y, ktorá obsahuje iba cesty lacnejšie ako cesta medzi X a Y. Aspoň jedna z týchto ciest toto pokazené optimálne riešenie opraví. Spraví ale aj niečo viac. Keďže pridaná cesta bola lacnejšia ako cesta, ktorú sme odstránili, vytvorili sme riešenie, ktoré je ešte lepšie ako optimálne riešenie. Ale to predsa nie je možné! Čo to znamená? Že sme sa pomýlili v úplne prvom predpoklade, ktorý tvrdil, že naše riešenie je zlé. Naše riešenie je teda naozaj správne a nájde najlacnejšie možné riešenie.
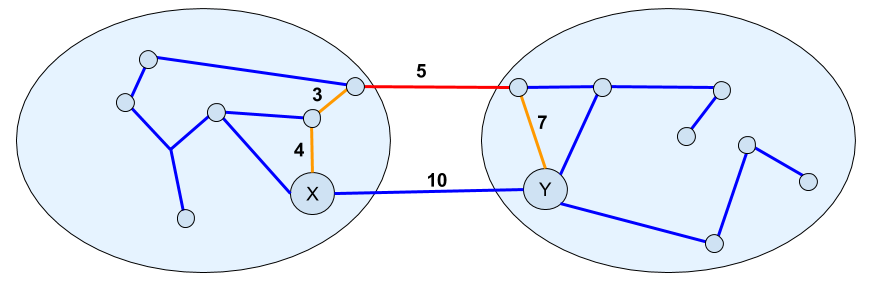
Na obrázku je znázornené to, čo som sa snažil vysvetliť v predchádzajúcom odstavci. Modrou farbou sú znázornené cesty, ktoré zrekonštruuje optimálne riešenie. Oranžové (a červená) cesty označujú trasu medzi mestami X a Y, ktoré obsahujú iba cesty lacnejšie ako priama cesta medzi týmito dvoma mestami. Takúto cestu nám zaručuje naše riešenie a fakt, že naše riešenie nerekonštruuje cestu medzi X a Y. Všimnite si, že ak vymeníme modrú cestu s cenou 10 za červenú cestu s cenou 5, dostaneme riešenie, v ktorom sa stále dá dostať odvšadiaľ všade, ale naviac je o 5 miliónov dolárov lacnejšie.
Záver
Problém, ktorý ste riešili v tomto príklade je problém grafový a volá sa hľadanie najlacnejšej kostry. A algoritmus, ktorý sme si tu predviedli sa skutočne používa, napríklad keď telekomunikácie potrebujú zistiť, kam zakopať káble tak, aby ich to vyšlo čo najlacnejšie, ale aj pri veľa iných problémoch. Názov tohto algoritmu je Kruskalov algoritmus.
V skutočnosti je ešte o chlp komplikovanejší. Aj keď nám ľuďom sa zdá podmienka ak sa dve mestá nachádzajú v rovnakom komponente vcelku jednoduchá a zrozumiteľná, počítačom to až tak jasné nie je. To čo ste vyriešili v tejto úlohe je preto iba polovica problému, druhá polovica sa zaujíma o to, ako má počítač zistiť, či sú dve mestá v tom istom komponente a ako to má zistiť dostatočne rýchlo. To však na riešenie tejto úlohy nebolo potrebné, možno si vás to nájde v nejakom ďalšom kole :)
Všimnite si, že tieto dve riešenia označujem ako naše a optimálne.↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.