Zadanie
Ak máte akékoľvek otázky ohľadom tejto úlohy, napíšte Edovi “Baklažánovi” Batmendijnovi na [email protected]
Pamätáte si ešte na blší cirkus?1 V tomto cirkuse majú obzvlášť veľké blchy, ktoré sa dajú trénovať. Minulý týždeň sa blšiemu cirkusu podarilo vyšľachtiť nový druh bĺch, ktoré sú ešte inteligentnejšie než tie staré a dajú sa s nimi robiť ešte zložitejšie predstavenia.
Pred blším vystúpením sa na zem nakreslí niekoľko (nepretínajúcich sa) kruhov a nejaké šípky medzi nimi. Každá šípka vedie od nejakého kruhu do nejakého (možno aj toho istého) kruhu. Ku každej šípke sa napíše buď jeden znak (písmeno alebo číslica), alebo sa nechá neoznačená, pričom musí platiť nasledovná vlastnosť: zo žiadneho kruhu nevedú von dve šípky označené rovnakým znakom, ani dve neoznačené šípky. Okrem toho sa jeden kruh označí ako štartovací a niektoré kruhy sa označia ako víťazné. Celé toto rozostavenie kruhov a šípok budeme nazývať schéma .
Samotné predstavenie vyzerá nasledovne: na začiatku sa jedna blcha postaví do štartovacieho kruhu a krotiteľ vyzve niektorého z divákov, aby mu niečo (v závislosti od druhu prestavenia to môže byť postupnosť písmen alebo číslic) napísal na papier. Toto niečo budeme nazývať vstupný text. Následne krotiteľ vstupný text nahlas číta znak po znaku. Vždy, keď krotiteľ prečíta nejaký znak, blcha urobí nasledovné:
- Najprv sa pozrie, či z kruhu, v ktorom práve stojí, vedie nejaká šípka označená znakom, ktorý krotiteľ práve prečítal. Ak áno, blcha skočí do kruhu, do ktorého vedie táto šípka.
- V prípade, že z kruhu kde blcha stála, neviedla žiadna šípka označená práve prečítaným znakom, blcha sa pozrie, či z neho vedie aspoň neoznačená šípka. Ak áno, blcha skočí pozdĺž tejto šípky.
- V prípade, že z kruhu kde blcha stála neviedla ani neoznačená šípka, blcha sa na to vykašle, vyskočí von z kruhu a predstavenie sa predčasne skončí.
Na konci predstavenia sa krotiteľ pozrie, v ktorom kruhu blcha skončila. Ak skončila v niektorom z víťazných kruhov, zablahoželá divákovi a dá mu lízatko.
Všimnite si, že to, v ktorom kruhu blcha skončí závisí iba na schéme a na vstupnom texte. Ak si teda vezmeme jednu konkrétnu schému, je pre ňu jednoznačne určené, pri ktorých vstupných textoch skončí blcha v niektorom z víťazných kruhov. Tieto vstupné texty budeme nazývať víťazné pre danú schému. V tejto úlohe budeme pre zadané množiny víťazných vstupných textov kresliť schémy.
Príklad
Skúsme nakresliť schému, pre ktoré sú víťazné všetky čísla deliteľné tromi (ktoré môžu prípadne začínať zbytočnými nulami) a už nič iné. Vieme, že číslo je deliteľné tromi práve vtedy, keď je jeho ciferný súčet deliteľný tromi. Ak by si teda blcha vedela pamätať, aký je súčet prečítaných cifier a na konci podľa toho skočiť do správneho kruhu, mali by sme vyhrané. Dokonca by nám stačilo, aby si stále pamätala, aký zvyšok dáva súčet doteraz prečítaných cifier po delení tromi. Ak by bol tento zvyšok na konci nula, blcha by skočila do nejakého víťazného kruhu, inak by skočila do nejakého iného kruhu.
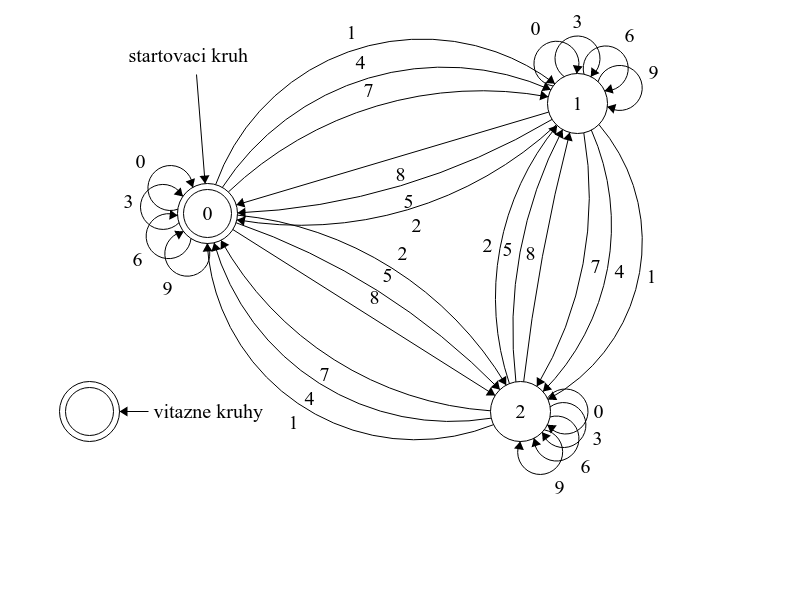
Blcha si, žiaľbohu, počas predstavenia nič nepamätá. Informáciu o zvyšku ciferného súčtu po delení tromi však môžeme mať počas predstavenia zakódovanú v pozícii blchy (teda v tom, v ktorom kruhu sa blcha práve nachádza). Môžeme teda nakresliť schému, ktorá bude mať tri kruhy (označme ich 0, 1 a 2). Pritom bude platiť, že:
- V kruhu 0 bude blcha vtedy, keď je súčet doteraz prečítaných cifier deliteľný tromi.
- V kruhu 1 bude blcha vtedy, keď súčet doteraz prečítaných cifier dáva zvyšok 1 po delení tromi.
- V kruhu 2 bude blcha vtedy, keď súčet doteraz prečítaných cifier dáva zvyšok 2 po delení tromi.
Z každého kruhu potom pôjde von 10 šípok označných ciframi 0 až 9. Šípky označené 0, 3, 6 a 9 budú vždy viesť do toho istého kruhu, lebo pripočítaním 0, 3, 6 alebo 9 sa zvyšok po delení troma nezmení. Šípky označené 1, 4 a 7 budú vždy viesť do kruhu s o 1 väčším číslom (resp. z kruhu 2 do kruhu 0), lebo pripočítaním 1, 4 alebo 7 sa zvyšok po delení tromi zvýši o 1. Nakoniec, šípky označené 2, 5 a 8 budú viesť do kruhu s o 1 nižším číslom (resp. z kruhu 0 do kruhu 2). Za štartovací označíme kruh 0, lebo keď sme ešte nič neprečítali, súčet prečítaných cifier je 0. Jediným víťazným kruhom bude opäť kruh 0, lebo číslo je deliteľné tromi vtedy, keď jeho ciferný súčet dáva po delení tromi zvyšok 0.
Súťažná úloha
(5 bodov) Nakreslite schému, pre ktorú budú víťazné všetky postupnosti znakov zložené z písmen
"a","b"a"c"také, že žiadne dve za sebou idúce písmená nie sú rovnaké. Žiadne iné postupnosti už víťazné byť nemajú. Teda napríklad postupnosť"abcbcbcbaba"má byť víťazná, ale postupnosť"bacca"nemá byť víťazná.(5 bodov) Nakreslite schému, pre ktorú budú víťazné postupnosti znakov, v ktorých sa niekde vyskytujú 4 á-čka po sebe. Teda napríklad slovo
"tadaaaa"má byť víťazné, ale slovo"lalalalalala"nemá byť víťazné.(5 bodov) Nakreslite schému, pre ktorú budú víťazné postupnosti znakov, v ktorých sa niekde (súvislo) vyskytuje slovo
"tamtamtatam"2 (pozor, nie slovo"tamtamtamtam"). Slovo"alotamtamtatambetam"je víťazné, ale slovo"tamverutamtatamtam"víťazné nie je.
V každej podúlohe okrem nakreslenia schémy aj zdôvodnite, prečo budú pre túto schému víťazné všetky postupnosti znakov špecifikované v danej podúlohe a prečo už žiadna iná postupnosť nebude víťazná. Nezabudnite vo vašich schémach vyznačiť štartovací kruh a víťazné kruhy.
O jeho vzniku sa môžete dočítať v zadaniach druhej série zimnej časti: https://prask.ksp.sk/ulohy/zadania/1107/ .↩
Takto sa totiž začína krotiteľova obľúbená pesnička.↩
Podúloha a)
Chceme, aby naša schéma kontrolovala, či sa vo vstupnom texte vyskytujú dve rovnaké písmená po sebe. Na to by sa nám hodilo pamätať si, aké písmeno bolo prečítané ako posledné. Keďže blcha nemá pamäť, budeme túto informáciu musieť zakódovať do pozície blchy. To môžeme urobiť napríklad tak, že budeme mať tri kruhy (označme ich \(A\), \(B\) a \(C\)), pričom:
- V kruhu \(A\) bude blcha práve vtedy, keď posledné prečítané písmeno bolo
"a"a zatiaľ nemáme dôvod myslieť si, že vstupné slovo nie je víťazné (teda krotiteľ doteraz neprečítal dve rovnaké písmená po sebe, ani neprečítal iné písmeno než"a","b"alebo"c"). - V kruhu \(B\) bude blcha vtedy, keď posledné prečítané písmeno bolo
"b"a vstupné slovo ešte môže byť víťazné. - V kruhu \(C\) bude blcha vtedy, keď posledné prečítané písmeno bolo
"c"a vstupné slovo ešte môže byť víťazné.
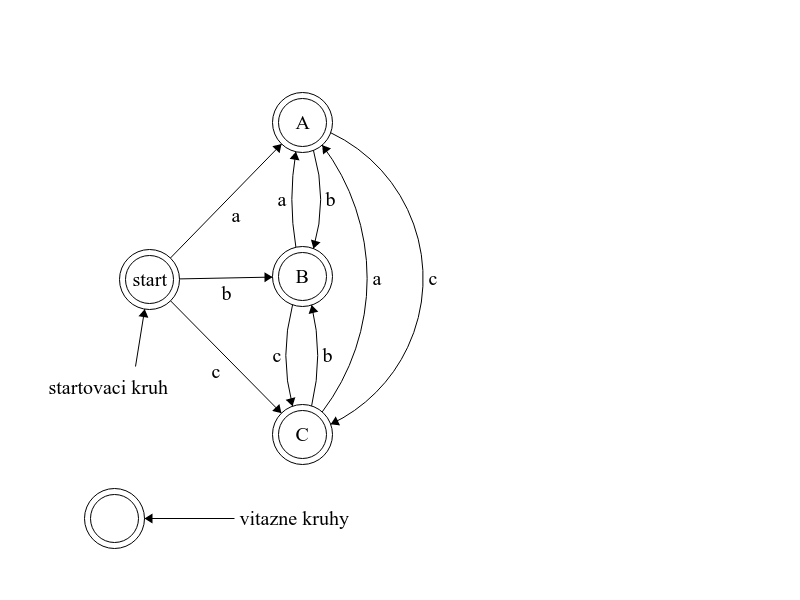
Na začiatku, keď ešte nebolo prečítané žiadne písmeno, by blcha nemala byť v žiadnom z kruhov \(A, B, C\), preto budeme mať okrem týchto troch kruhov štvrtý, štartovací. Zo všetkých kruhov okrem \(A\) nakreslíme šípku označenú "a" do kruhu \(A\), zo všetkých kruhov okrem \(B\) nakreslíme šípku označenú "b" do kruhu \(B\) a zo všetkých kruhov okrem \(C\) nakreslíme šípku označenú "c" do kruhu \(C\). Takto sa bude blcha počas predstavenia vždy nachádzať v správnom kruhu podľa toho, čo krotiteľ prečítal ako posledné.
Keď je blcha v kruhu \(A\) a krotiteľ prečíta písmeno "a", znamená to, že vo vstupnom texte boli dve "a"-čka po sebe. V takom prípade teda vieme, že vstupný text nemá byť víťazný. Preto nemá zmysel pokračovať v predstavení a blcha sa na to môže rovno vykašľať. Z kruhu \(A\) teda nenakreslíme žiadnu šípku označnú "a" (a ani žiadnu neoznačenú šípku). Podobne nenakreslíme šípku označenú "b" z kruhu \(B\), ani šípku "c" z kruhu \(C\). Takýmto spôsobom zaručíme, že vo všetkých zlých prípadoch blcha vyskočí von zo schémy – aj v prípade, že krotiteľ prečíta nejaké iné písmeno než "a", "b" a "c", aj v prípade, že sú vo vstupnom texte dve rovnaké písmená za sebou. V schéme teda blcha ostane až do konca predstavenia iba pri víťazných textoch, preto všetky štyri kruhy označíme ako víťazné.
Podúloha b)
Tentoraz si potrebujeme pamätať, či posledné prečítané písmená boli "a"-čka, a ak áno, koľko za sebou ich bolo. Okrem toho si v prípade, keď krotiteľ prečíta štyri "a"-čka po sebe, potrebujeme zapamätať, že vstupný text je určite víťazný. Nakreslíme si teda \(5\) kruhov, označme ich \(0, 1, 2, 3\) a “výhra”. V kruhu s číslom \(x\) bude blcha práve vtedy, keď posledných \(x\) prečítaných písmen boli "a"-čka a písmeno pred tým nebolo "a". Kruh “výhra” bude víťazný kruh, do ktorého blcha skočí vtedy, keď krotiteľ prečíta \(4\) "a"-čka po sebe a z tohto kruhu už potom nikdy nevyskočí von. Keď bude blcha v kruhu s nejakým číslom a krotiteľ prečíta "a", znamená to, že počet po sebe prečítaných "a"-čok sa zväčšil o \(1\), teda blchu necháme skočiť do kruhu s o \(1\) väčším číslom (z kruhu číslo \(3\) ju necháme skočiť do kruhu “výhra”, lebo štyri "a"-čka znamenajú víťazné slovo). Ak je blcha v číslovanom kruhu a krotiteľ prečíta niečo iné ako "a", znamená to, že v tomto momente je z posledných prečítaných písmen nula "a"-čok, teda ju necháme skočiť do kruhu \(0\). Kruh \(0\) bude zároveň aj štartovací.
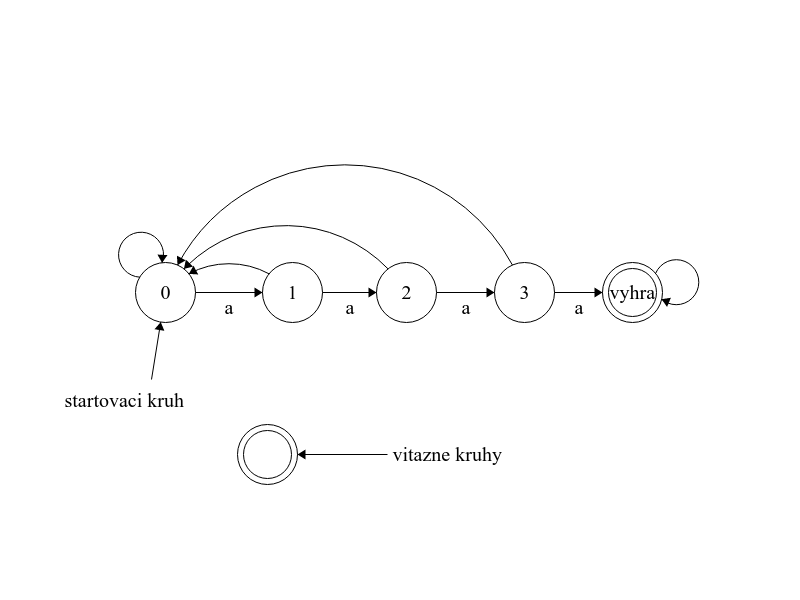
Predstavenie teda bude vyzerať tak, že vždy, keď bude krotiteľ čítať "a"-čka, blcha bude postupovať smerom ku víťaznému kruhu a vždy, keď prečíta niečo iné, blcha “padne” späť na nulu. Ak krotiteľ niekedy prečíta \(4\) "a"-čka po sebe, blche sa podarí dostať do víťazného kruhu a tam ostane až do konca predstavenia.
Podúloha c)
Táto podúloha sa dosť podobá na tu predošlú, čo by nás mohlo navádzať na podobné riešenie: nakreslíme si \(12\) krúžkov očíslovaných \(0\) až \(11\) (keďže slovo "tamtamtatam" má jedenásť písmen), pričom v krúžku s číslom \(x\) bude blška vtedy, keď sa poslených \(x\) prečítaných písmen zhoduje s prvými \(x\) písmenami slova "tamtamtatam". Krúžok \(11\) označíme ako víťazný a nakreslíme mu neoznačenú šípku do neho samého, takže keď sa tam blcha raz dostane, už odtiaľ neujde. Celé by to teda mohlo vyzerať takto:
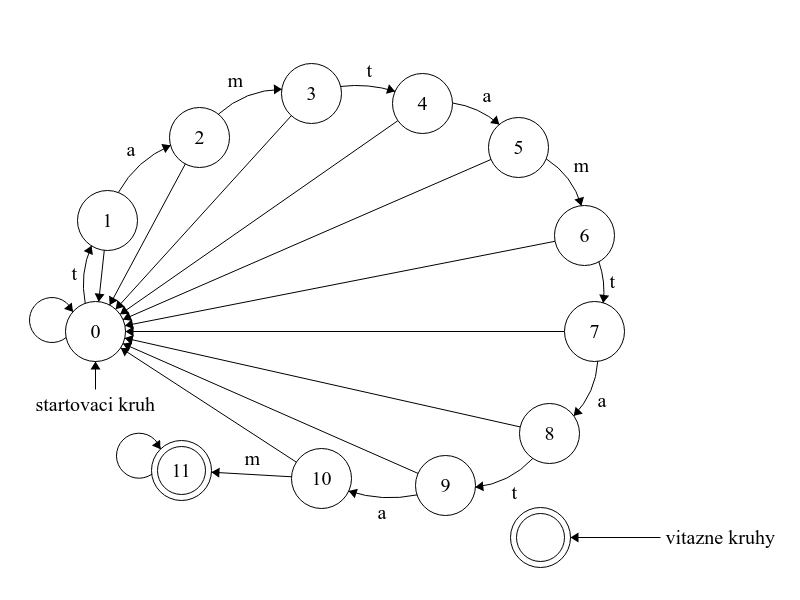
Mnohí z vás sa vo svojich riešeniach dopracovali presne sem. Toto riešenie však ešte nie je správne. Predstavte si, čo by sa stalo, ak by vstupný text bol "ttamtamtatam". Po prečítaní prvého "t" by blcha skočila do krúžku \(1\), po prečítaní druhého "t" by ale skočila do kruhu \(0\), kde by ostala aj na najbližšie dve písmená "am", následne by počas čítania ďalších 5 písmen "tamta" doskákala do kruhu \(5\), ale potom by pri prečítaní "t" padla opäť na \(0\) a tam by ostala až do konca. Text "ttamtamtatam" v našej schéme teda nie je víťazný, napriek tomu, že obsahuje slovo "tamtamtatam".
Ako sa s týmto problémom vysporiadať? Prvý spôsob, ktorý by nám mohol napadnúť, je dokresliť zo všetkých krúžkov (okrem kruhu \(11\)), z ktorých nevedie šípka označená "t", šípku do kruhu \(1\) označenú "t". To síce pomôže pri vstupnom texte "ttamtamtatam", ale nevyrieši to úplne všetko. Skúste si napríklad rozmyslieť, čo by sa v takejto schéme stalo, ak by vstupné slovo bolo "tamtamtamtatam". Mohli by sme naše riešenie skúšať plátať ďalej, ale to väčšinou nie je tá správna cesta pri riešení problémov: riešenie by sa stávalo čoraz zložitejším a ľahko by sme mohli na niektoré prípady zabudnúť.
Lepšie je postupovať systematicky. Najprv si poriadne definujeme, kedy má byť blcha v ktorom kruhu:
- V kruhu \(11\) bude blcha vtedy a len vtedy, ak v tom, čo už krotiteľ prečítal, niekde bolo celé slovo
"tamtamtatam". - V akomkoľvek inom kruhu číslo \(x\) bude blcha vtedy a len vtedy ak je číslo \(x\) najväčšie číslo, pre ktoré platí nasledovná vlastnosť:
- Posledných \(x\) písmen, ktoré krotiteľ prečítal sa zhoduje s prvými \(x\) písmenami slova
"tamtamtatam".
"ratatamtam", blcha nebude v kruhu \(3\), ale v kruhu \(6\). Je síce pravda, že posledné \(3\) prečítané písmená sa zhodujú s prvými troma písmenami"tamtamtatam", ale aj posledných \(6\) písmen sa zhoduje a \(6\) je viac ako \(3\). - Posledných \(x\) písmen, ktoré krotiteľ prečítal sa zhoduje s prvými \(x\) písmenami slova
Ako teraz správne nakresliť šípky? Prvá vec, ktorú si môžeme uvedomiť, je nasledovná: ak je blcha v nejakom momente v kruhu číslo \(x\) a \(x > 0\), o písmeno skôr musela byť v kruhu s číslom minimálne \(x-1\): ak sa totiž teraz posledných \(x\) prečítaných písmen zhoduje s prvými \(x\) písmenami "tamtamtatam", o písmeno skôr sa určite zhodovalo posledných \(x-1\) písmen. To okrem iného znamená, že zo žiadneho kruhu sa nedá na jeden skok dostať do kruhu, ktorého číslo by bolo väčšie o \(2\) alebo viac. Z každého kruhu teda pôjde jedna šípka do kruhu s o \(1\) vyšším číslom a všetky ostatné šípky pôjdu do kruhov s menšími číslami. Šípky postupujúce do kruhov s väčšími číslami teda budú vyzerať rovnako ako v pôvodnom riešení. Zaujímavejšie sú šípky vedúce dozadu.
- Ak je blcha v kruhu \(1\), posledné prečítané písmeno muselo byť
"t".- Ak krotiteľ prečíta
"t", posledné dve písmená budú"tt", čo znamená, že posledné písmeno sa zhoduje s prvým písmenom"tamtamtatam", ale viac ako jedno sa určite nezhoduje. Preto by v takom prípade blcha mala skočiť naspäť do kruhu \(1\). - Ak ktoriteľ prečíta čokoľvek iné ako
"t"alebo"a", posledné prečítané písmeno nebudet, teda blcha by mala skočiť do kruhu \(0\).
- Ak krotiteľ prečíta
- Ak je blcha v kruhu \(2\), posledné dve prečítané písmená boli
"ta".- Ak krotiteľ prečíta
"t"m posledné tri písmená budú"tat", čo znamená, že blcha bude musieť skočiť do kruhu \(1\). - Ak krotiteľ prečíta čokoľvek iné ako
"t"alebo"m", blcha skočí do kruhu \(0\).
- Ak krotiteľ prečíta
- Ak je blcha v kruhu \(3\), posledné tri písmená boli
"tam". Ak krotiteľ prečíta čokoľvek iné ako"t", žiadny nenulový počet posledných prečítaných písmen sa nebude zhodovať so začiatkom slova"tamtamtatam". Preto blcha skočí do kruhu \(0\). - Pre kruhy \(4, 5\) a \(7\) bude situácia podobná ako pre kruh \(2\), pre kruh \(6\) zasa ako pre kruh \(3\). Zaujímavý moment ale príde pri kruhu \(8\).
- Ak je blcha v kruhu \(8\), posledné prečítané písmená sú
"tamtamta".- Ak teraz krotiteľ prečíta
"m", posledných 9 písmen bude"tamtamtam", teda až \(6\) posledných písmen sa bude zhodovať s prvými \(6\) písmenami"tamtamtatam". Preto vtedy blcha skočí do kruhu \(6\). - Ak krotiteľ prečíta čokoľvek iné ako
"t"alebo"m", blcha skočí do kruhu \(0\).
- Ak teraz krotiteľ prečíta
- Pre kruhy \(9\) a \(10\) bude situácia rovnaká ako pri kruhu \(2\).
Celá schéma teda bude vyzerať nasledovne:
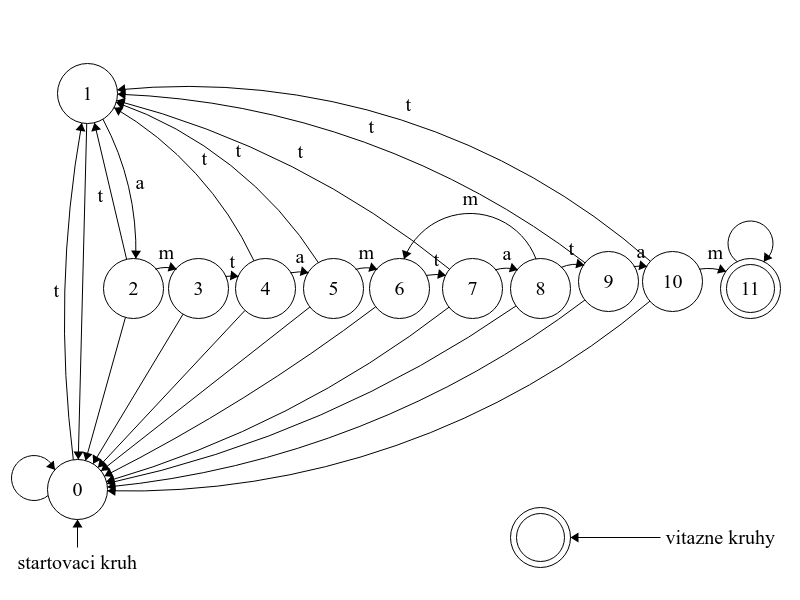
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.