1. Princova dilema vzorové riešenie

Najľahšia gulička

Zamyslime sa najprv, ako by sme hľadali najľahšiu guličku.

Prvý spôsob by bol taký, že si vyberieme ľubovoľnú guličku a povieme si, že je to náš favorit na najľahšiu guličku. Teraz favorita porovnáme s inou guličkou. Čo sa môže stať? Nová gulička je ľahšia ako favorit. Favorit už nemôže byť tou najľahšou guličkou a teda ho musíme zmeniť. Novým favoritom sa stane gulička ktorá porazila toho predošlého. Ak je ale pôvodný favorit ľahší, znamená to, že stále má šancu stať sa nakoniec tou najľahšou guličkou a teda si ho ponecháme. Naviac gulička, s ktorou sme ho porovnávali, nemôže byť najľahšia gulička. Keď toto porovnanie s favoritom a prípadnú výmenu urobíme s každou guličkou, na konci bude favoritom tá najľahšia gulička zo všetkých.

Druhý spôsob je trochu zložitejší. Usporiadame medzi guličkami turnaj. Najprv všetky guličky rozdelíme na dvojice, medzi nimi usporiadame zápasy (porovnania) a do ďalšieho kola postúpi z každého zápasu tá ľahšia gulička. Takže zo šestnástich guličiek nám ostane 8. V druhom kole opäť popárujeme tieto zostávajúce guličky, porovnáme zápasiace guličky a postúpia len 4. Toto opakujeme, až kým nám v kole nezostane len jedna gulička, ktorá je zároveň tou najľahšou, keďže najľahšia gulička porovnanie nikdy neprehrá.

Koľko porovnávaní potrebujú tieto spôsoby? V prvom spôsobe každú guličku (okrem jednej – tej, ktorá je favorit na začiatku) raz porovnáme a možno vymeníme s favoritom, teda urobíme 15 porovnaní. Keby sme mali \(n\) guličiek, použili by sme \(n-1\) porovnaní. V druhom spôsobe sme si v každom kole rozdelili guličky do dvojíc a v každej dvojici sme urobili jedno porovnanie. Ak bolo v kole \(k\) guličiek, urobili sme v tomto kole \(k/2\) porovnaní. Zároveň do ďalšieho kola postúpi len polovica guličiek. V našom príklade by bolo v prvom kole 16 guličiek, v druhom 8, v treťom 4, v štvrtom 2 a potom už máme určeného víťaza. Ak tieto počty vydelíme dvoma a sčítame, dostaneme celkový počet porovnaní, a to je \(8+4+2+1=15\). Pre všeobecný prípad s \(n\) guličkami to je \(n/2 + n/4 + n/8...+1 = n-1\).¹ Takže oba spôsoby sú rovnako dobré.

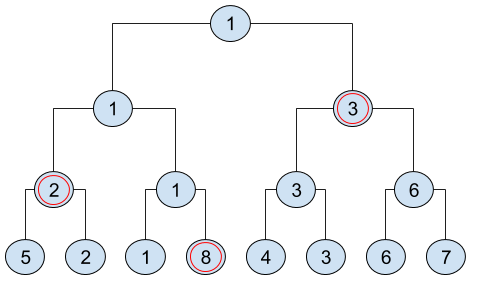
Na obrázku si môžete pozrieť turnaj s 8 guličkami, čísla v krúžkoch sú váhy guličiek. Červenou sú zvýraznené všetky guličky, ktoré prehrali s najľahšou guličkou – potenciálne druhé najľahšie guličky.

Druhá najľahšia gulička

Ako nájsť druhú najľahšiu guličku? Skúsime sa odraziť od spôsobov na nájdenie tej najľahšej. V oboch spôsobov sme robili zápasy, ale iným spôsobom. V prvom išiel do zápasu vždy favorit a nová gulička, v druhom sme na to išli kolami. Dôležité pozorovanie je, že druhú najľahšiu guličku musela v zápase poraziť tá najľahšia gulička. Nad ostatnými totiž druhá najľahšia gulička zápas určite vyhrá. Stačí nám teraz nájsť tú najľahšiu guličku spomedzi tých, ktoré porazila tá úplne najľahšia. Koľko najviac takýchto guličiek môže byť?

Ak sme našli najľahšiu guličku prvým spôsobom, v najhoršom prípade sa nám mohlo stať, že sme si na začiatku vybrali ako favorita práve tú najľahšiu guličku, ktorá následne porazila všetky zvyšné guličky. V tomto prípade by sme teda museli nájsť najľahšiu spomedzi 15 guličiek, na čo by sme potrebovali 14 porovnaní. Všobecne, z \(n\) guličiek nám zostalo \(n-1\) a potrebovali by sme teda \(n-2\) porovnaní.

V druhom spôsobe tá najľahšia gulička mohla vyhrať omnoho menej zápasov, keďže v každom kole zápasila len raz. Koľko bolo kôl? V našom prípade bolo kolo so 16 guličkami, 8, 4 a 2. Len 4 kolá, to znamená, že musíme vybrať najľahšiu už len spomedzi štyroch guličiek, na čo nám stačia 3 porovnania. Na to, aby sme určili počet porovnaní pre všeobecný prípad, musíme vypočítať, koľko bude vo všeobecnom prípade kôl. V každom kole sa počet guličiek zmenší na polovicu až kým nezostane len jedna gulička. Takže kôl pre číslo \(n\) je toľko, koľko krát by sme vedeli vydeliť \(n\) dvojkou. Ak predpokladáme, že \(n=2^k\), tak sa odohrá \(k\) kôl.

Pre všeobecné \(n\) existuje matematická funkcia logaritmus, pre ktorú platí \(n=2^{\log_{2}(n)}\),², teda \(\log_{2}(n) = k\). Počet kôl je teda \(\log_{2}(n)\). Takže musíme nájsť tú najľahšiu spomedzi \(\log_{2}(n)\) guličiek, na čo potrebujeme \(\log_{2}(n) - 1\) porovnaní.

Týmto spôsobom sme použili \(n-1\) porovnaní na nájdenie najľahšej guličky, a \(\log_{2}(n) - 1\) na nasledovné hľadanie druhej najľahšej guličky. Dokopy teda použijeme \(n+\log_{2}(n) - 2\) porovnaní, v našom prípade teda 18.